串级PID及角度过零处理

本文针对RoboMaster Can通讯电机而写，机械角度为0-8191，也可推广到其他电机使用。

一、为什么需要过零处理

原因：防止过零误差对角度PID的控制量输出产生不可控影响

一般来说，想让电机停止在某一确定位置，最常用的控制方法就是串级PID。串级PID原理这里不照本宣科，我们更应该关注它是如何“串起来”实现对电机控制的。

首先，我们来看一下位置式PID的公式（如下图）。从公式中易知，PID输出的控制量就是误差及误差变换的线性组合，为了方便讨论，我们令积分项和微分项为0，得到纯P控制下的公式：

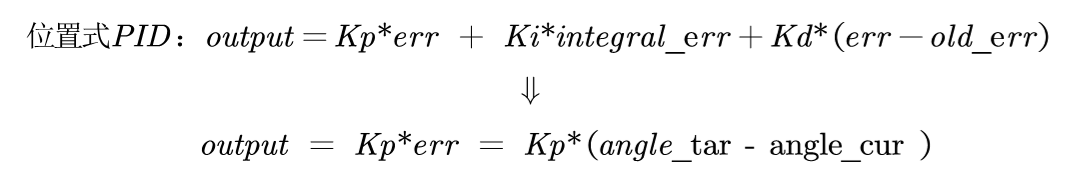
PS：
angle_tar：目标角度值
angle_cur: 当前角度值
angle_output : 角度环控制量
angle_err = angle_tar - angle_cur

speed_tar：目标速度值
speed_cur: 当前速度值
speed_output : 速度环控制量

定义：顺时针方向旋转为正方向。电机默认状态为静止，即speed_cur为0。
如下图所示：将angle_output赋值给速度环的speed_tar就实现了“串起来”。这理解起来不难，
当角度无误差时，速度环的目标值就是零，电机保持不动；
当角度误差为正时，angle_output与speed_output为正，电机正转；
当角度误差为负时，angle_output与speed_output为负，电机反转。
根据PID公式，角度误差越大，speed_tar就越大，则速度误差越大，电机就以越快的速度接近目标角度。换言之，就是角度有误差电机就动，直到达到目标角度位置为止。

当电机过机械零点时，实际的角度误差很小，但测量的角度误差却多了一个周期的角度，从而使速度环输出较大的控制量，电机就会以极高的速度旋转。当每次过零都没有经过处理时，电机就会越转越快，从而失控。因此，过零处理就是要避免这种情况的发生。

二、如何进行过零处理

首先要明白过零处理的本质：数学上的运算
这种运算的结果可以将一个绝对值较大的误差转换成绝对值较小的反向误差

电机角度的变化可以分为如下四种情况：其中情况（1）和（3）都没有过零，正常的PID运算是我们想要的结果。（2）属于8191–>0的过零情况，遇到这种情况我们应当让测量值多减去一个周期的角度，再进行PID计算。（4）属于0–>8191的过零情况，遇到这种情况我们应当让测量值加上一个周期的角度，再进行PID计算。

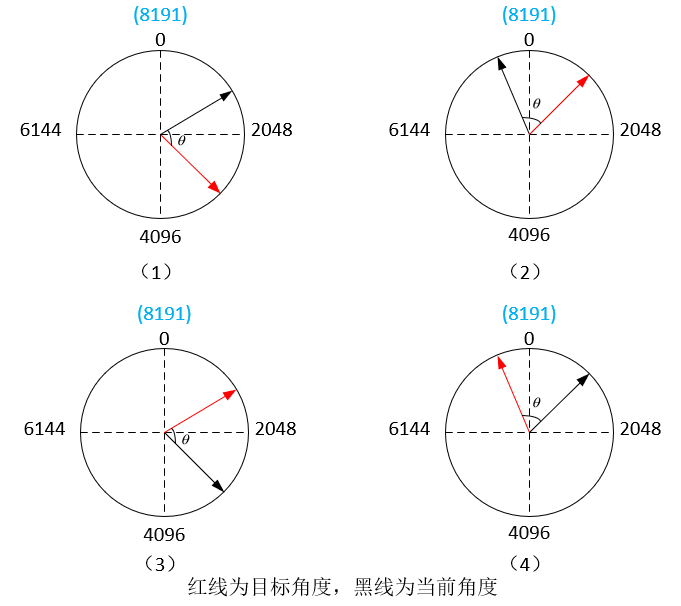
有无角度过零处理电机旋转情况对比如下：

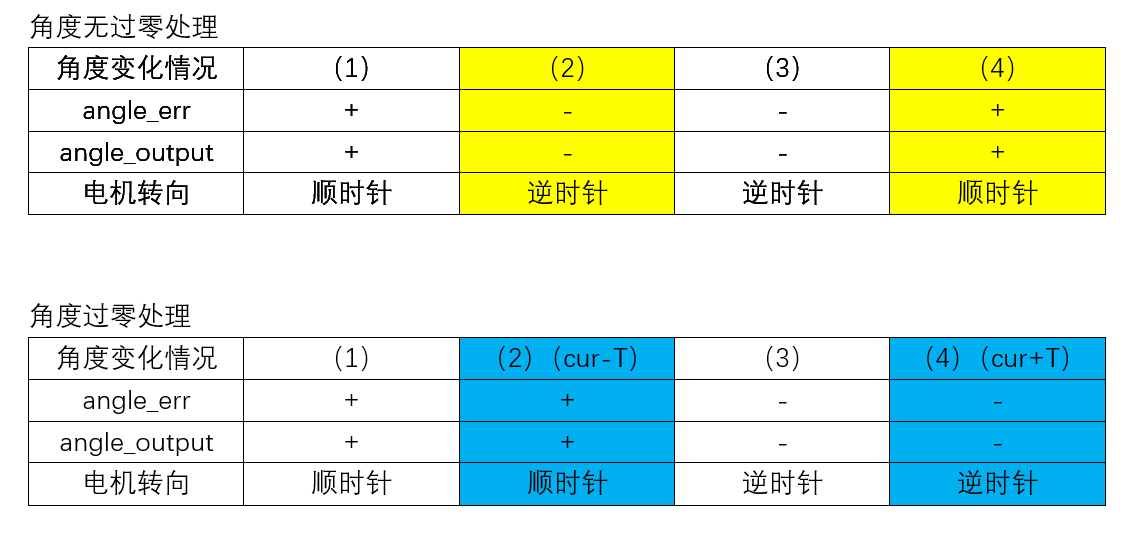
对比两个表，在无过零处理情况时，情况（2）和（4）的电机会以一个较长的路径到达目标角度（如果在这路径中过零，那电机就疯了），这不是我们想要的结果，我们总是希望电机以较短的路径到达目标角度位置。

通过将测量到的角度值加上或减去一个周期，就可以将一个绝对值较大的误差转换成绝对值较小的反向误差（即消除过零突变产生的误差），通过反向误差，速度环就会输出一个反向控制量使电机以反方向到达目标角度位置。

请看下图：

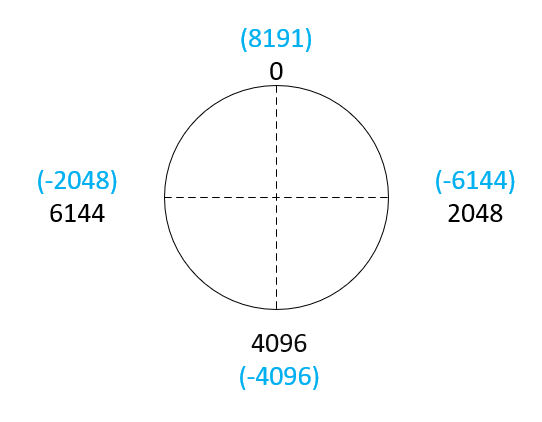
电机的位置，是不是可以用其他非测量到的数值表示？

将测量到的角度值加上或减去一个周期，背后的原理就是用“另外一个值”来表示电机当前的位置。并且只有在过零情况时，才需要用“另一个值”来表示。我用殊途同归，来概括这种方法，殊途即不同的电机位置表示确定出电机到达目标位置的不同路径，同归当然就是同一个目标角度位置了。

三、举个例子

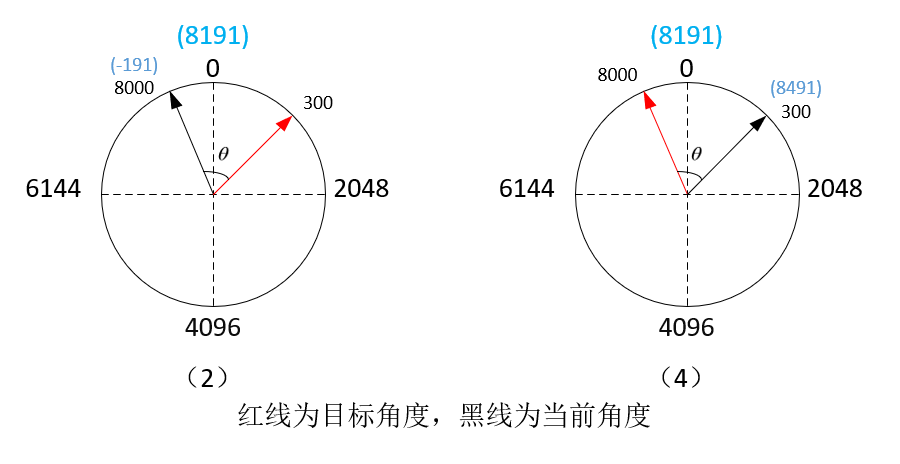
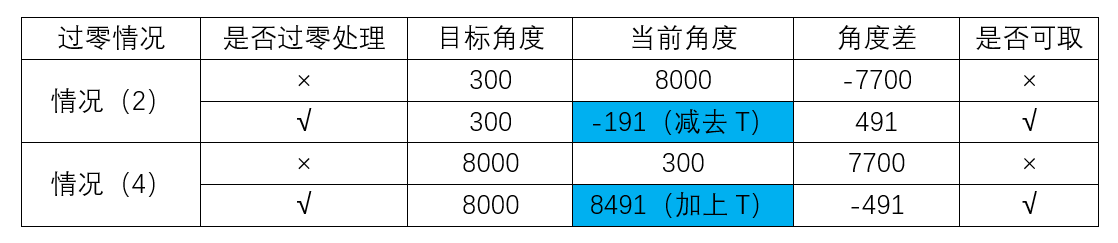
是不是实现了将一个绝对值较大的误差转换成绝对值较小的反向误差的效果？

四、代码实现

最后一个问题，我们如何判断电机是否过机械零点？
很简单，当目标角度与当前角度差值的绝对值大于半圈机械角度时，即判断处于过零情况发生！

啊？ 没过零点不是也存在目标角度与当前角度差值的绝对值大于半圈的机械角度的情况吗？

答：这种情况的角度是渐变的，而过零角度是突变的，两者有本质的区别。渐变的情况下，电机往目标角度旋转时的误差是逐渐减小的，而突变情况下的误差一直存在，需要人为消除。

/* 角度Pid时，在更新tar和cur之后紧接着调用, 处理完再进行PID计算*/
void Handle_Angle8191_PID_Over_Zero(float *tar, float *cur)
{
	if(*tar - *cur > 4096)    //4096 ：半圈机械角度
	{
		*cur += 8192;        //8191,8192无所谓了，四舍五入
	}
	else if(*tar - *cur < -4096)
	{
		*cur = *cur - 8192;
	}
	else
	{
		//*cur = *cur;
		// do nothing
	}
}