前言:
本专栏旨在记录高频笔面试手撕代码题,以备数字前端秋招,本专栏所有文章提供原理分析、代码及波形,所有代码均经过本人验证。
目录如下:
10.数字IC手撕代码-数据位宽转换器(宽-窄,窄-宽转换)
13.数字IC手撕代码-流水握手(利用握手解决流水线断流、反压问题)
18.数字IC手撕代码-双端口RAM(dual-port-RAM)
...持续更新
为了方便可以收藏导览博客: 数字IC手撕代码-导览目录
目录
格雷码介绍
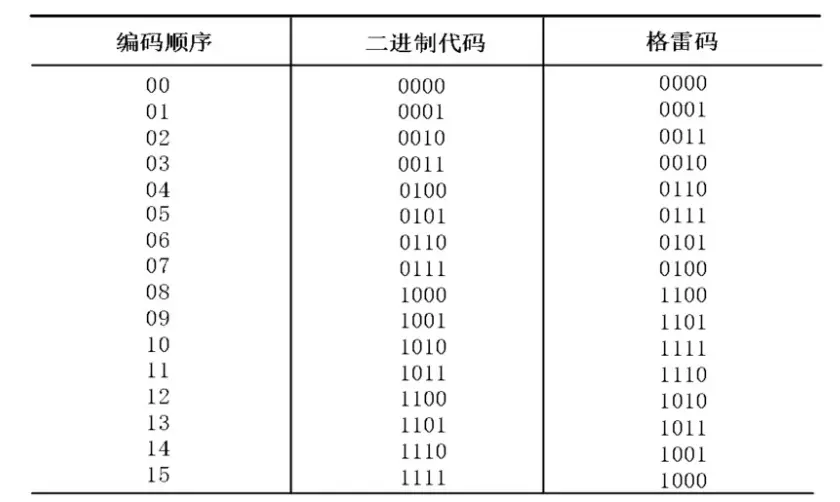
格雷码的主要特点是相邻编码值中只有一个比特发生改变,如下表所示。

从表中可以看到,相邻编码值中只有一个比特发生改变,那么这个特性有什么用呢?
这非常重要!
当今格雷码被广泛应用于 使用两个不同时钟的异步FIFO(First In First Out,先入先出存储器)中。当数值从一个时钟域传递到另一个时钟域时,单比特翻转的特性就会变得极为重要。
在异步FIFO中,写地址和度地址是根据读写操作,发生连续的改变,其地址是用二进制计数器进行表示的。以4比特计数器为例,该计数器从0计数,数到15,到达15后归零。在FIFO里,首先我们要使用转换公式把二进制编码转换成格雷码,并使用格雷码值从一个时钟域传递到另一个时钟域,然后使用另一个转换公式将格雷码转换为二进制码。

当多比特位宽的信号从一个时钟域到另一个时钟域时,需要使用上面电路。开始时,信号转换成格雷码,然后进入CLKA时钟域的寄存器。此后,通过两级同步器(称为打两拍)同步到目的时钟域。实现同步后,通过相反的译码过程(gray2bin)就可以实现多比特在两个时钟域之间的传递,看似繁琐,但这一转换是必要的!

比如三比特的二进制进行跨时钟域转换。当CLKA时钟域中,数值从5变到6时,经同步器后,目的时钟域的格雷码变为101,或者因为延迟,数值没有改变,格雷码还是111,要等到下一个周期(第三拍)之后才能变成101。可以看出,无论是101还是111,最终传递的结果都是按照顺序出现合法的编码值。假如不使用这种二进制-格雷码、格雷码-二进制的转换电路,直接在CLKB时钟域打两拍接收数据会出现什么情况呢?

经过两级同步后,同步之后的二进制值可能是101(旧值)、110(新值),但也可能变成100或者111(因为打两拍过程是为了解决亚稳态,而信号翻转时的亚稳态不确定采样到0还是采样到1,所以低两位变化结果不确定)。由于两个时钟相互独立,同步器输入的两个比特分别进行跨时钟域同步,这些独立同步并输出的值可能出现在不同的时钟周期上。
虽然最终所有比特会输出正确的值,并且最终输出将变为110。然而,在转变过程中,可能输出违反计数规则的值,这是极其致命的。
对于FIFO来说,其空、满状态是根据其内部数据深度进行判断得到的,当出现这些临时的非法值时,FIFO可能会产生错误的空、满状态,从而造成外部电路对其内部存储数据量的错误判断,把一个有数据的FIFO认为是空,把一个未满的FIFO认为是满,造成系统错误,甚至奔溃。
说了那么多,我们已经知道为什么格雷码很重要,以及格雷码的用途(异步FIFO数据传输),下面我们来给出格雷码和二进制相互转换的模块。
binary_to_gray
二进制转换格雷码机制:格雷码的最高位和二进制的最高位是一样的,格雷码的其他位可以用二进制对应位和相邻高位的异或得到,即
assign gray_value[ i ] = binary_value[ i ] ^ binary_value[ i + 1 ];
比对一下格雷码二进制转换表,符合我们上面说的规律,知道转换原理,写代码就简单了。
代码
module binary_to_gray#(
parameter WIDTH = 4
)(
input [WIDTH-1:0] binary_value ,
output [WIDTH-1:0] gray_value
);
genvar i;
generate
for(i=0;i<(WIDTH-1);i=i+1)begin
assign gray_value[i] = binary_value[i] ^ binary_value[i+1];
end
endgenerate
assign gray_value[WIDTH-1] = binary_value[WIDTH-1]; // highest bit
endmoduletestbench
module binary_to_gray_tb#(
parameter WIDTH = 4
)(
);
wire [WIDTH-1:0] gray_value;
reg [WIDTH-1:0] binary_value;
initial begin
binary_value <= 4'b0000;
end
always #5 binary_value <= binary_value + 1'b1;
binary_to_gray u_binary_to_gray(
.gray_value (gray_value) ,
.binary_value (binary_value)
);
endmodule
波形

gray_to_binary
格雷码转二进制也是一样的道理,二进制最高位和格雷码最高位一致。二进制的其他位可以由格雷码对应位对应二进制的相邻高位的异或得到。用公式表示即:
Binary[n] = Gray[n];
Binary[n-1] = Binary[n] ^ Gray[n-1];
代码
module gray_to_binary#(
parameter WIDTH = 4
)(
output [WIDTH-1:0] binary_value ,
input [WIDTH-1:0] gray_value
);
genvar i;
generate
for(i=WIDTH-1;i>=1;i=i-1)begin
assign binary_value[i-1] = binary_value[i] ^ gray_value[i-1];
end
endgenerate
assign binary_value[WIDTH-1] = gray_value[WIDTH-1]; // highest bit
endmodule
testbench
module gray_to_binary_tb#(
parameter WIDTH = 4
)(
);
reg [WIDTH-1:0] gray_value;
wire [WIDTH-1:0] binary_value;
initial begin
gray_value <= 4'b0000;
end
always #5 gray_value <= gray_value + 1'b1;
gray_to_binary u_gray_to_binary(
.gray_value (gray_value) ,
.binary_value (binary_value)
);
endmodule
波形

所有结果都和我们设计的一样,好,以上就是格雷码转二进制及二进制转格雷码的全部内容。








 本文详细介绍了格雷码及其与二进制之间的转换方法。解释了格雷码的特点及其在异步FIFO中的应用,提供了具体的Verilog代码实现,并通过波形验证了转换的正确性。
本文详细介绍了格雷码及其与二进制之间的转换方法。解释了格雷码的特点及其在异步FIFO中的应用,提供了具体的Verilog代码实现,并通过波形验证了转换的正确性。


















 663
663

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










