本文深入探讨了ROS2 Nav2中的RPP（受控纯追踪）控制器算法，从纯追踪（Pure Pursuit）算法原理出发，分析了RPP算法的优化方向和存在的问题。通过对Nav2_controller子目录和nav2_regulated_pure_pursuit_controller源码的理解，揭示了算法如何处理路径规划、速度控制和碰撞检测。文章指出了拐点略过、坐标获取和路径规划错误可能存在的问题，并提出了分析方法和潜在解决方案。
1 引入
项目的阿克曼小车，在接近终点时如果角度有偏差，或者途中需要做大角度的调整（主要涉及到倒车的情况）时的行动总是不理想。所以，现在开始从控制器算法入手尝试去优化。本文会沿着从算法原理-源码理解-分析调整-最终改进的道路，记录项目的进程，欢迎留言指正和讨论。
2 PP（ Pure Pursuit)算法
2.1 算法原理
为便于理解，本文从PP（ Pure Pursuit)算法开始，参见附件第二篇（Implementation of the Pure Pursuit Path Tracking Algorithm）
- 2.1.1 基本思路：
如上图，以机器人为中心 （ P r ） （P_{r}） （Pr），画一个圆（半径L可以是固定，也可以根据速度调整），圆与规划的路径交点为前瞻（lookahead）点 P l P_{l} Pl，控制器以机器人当前点与前瞻点的连线，作为目标运动命令（线速度+角速度）的计算和发布，驱动机器人始终追踪规划好的路径。 - 2.1.2 计算：
阿克曼车（前轮转向）小车的运动计算中心在后轮轴上，要从当前位置运动到前瞻点位置，需要计算的是旋转半径 r r r（这里后面会根据阿克曼的结构写详细些 — Nav2导航中的阿克曼计算），如以小车后轮中心为原点，前瞻点的坐标变换为（x,y），从上图可以得到：
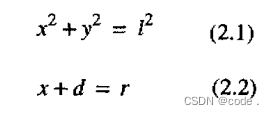
- 公式2.1是因为前瞻点到小车位置的距离是 l l l，而得到的。
- 公式2.2 指出要计算小车原点到旋转中心的距离 r r r，还需要再求出 d d d。而 d d d的计算，可以按下面步骤：
可见控制小车运动的曲率（旋转半径的倒数），与前瞻与点当前位置的X偏差有关，注意这个X是指小车坐标系的X方向，不是地图的X方向。
- 2.1.3 算法流程
- 确定小车当前坐标.
- 找到规划的路径中距离小车最近的点. (后面将从这点开始沿着路径找到第一个目标点，避免向后找，搞错方向)
- 找到目标点（前瞻点） 。（从前面那个点沿着路径往后找到第一个距离小车当前位置大于等于前瞻距离l的路径点）
- 将目标点的坐标转换到小车坐标系
- 计算曲率和发送命令让小车方向对准该曲率
- 更新小车坐标
2.2 算法特性
- 改变前瞻距离的影响
在要考虑两种不同的情况：
（1) 重新获取路径：小车距离路径太远，需要重新获取路径
（2) 保持路径：小车基本就在路径上，希望继续保持原规划路径。
在第（1)种情况下，前瞻距离大可以使得小车更为平顺的汇入路径，减少反复的振荡调整（如上图）。
第（2)种情况下，前瞻距离越大，路径上的弯曲就越少能被追踪到。如果小车到目标点之间特别弯曲，没法用一个圆弧完成连接，就会导致错误的驱动。
2.3算法优化方向
显然基于前述特性，需要找到一种方法，使得前瞻距离能与路径的弯曲程度匹配。
可论文提出（过程原文有，在此不赘述）：可以从前瞻距离得到旋转半径，但没法反过来从路径的曲率半径得到确定的前瞻距离。所以给出结论是：用路径的曲率半径的1-2倍作为前瞻距离都是合理的。（这是1992年论文，再看看后面吧）
2.4 算法的问题
算法没有考虑小车或者执行器的能力属性，只是假定它能理想的响应到要求的曲线。这会导致两个问题：
1） 在高速的情况下可能会发出急转弯的控制要求，会导致小车尾部打滑（漂移？）
2）小车没有期望的那么快靠近路径，因为会有转向的一阶滞后
2.5 算法变体
- Adaptive Pure Pursuit (APP)：MIT提出依照平移速度按比例改变前瞻距离 L t L_{t} Lt。
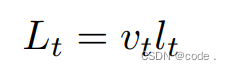
v t v_{t} vt是速度， l t l_{t} lt是系数（反映预期以当前速度运动到前瞻点的时间）。
3 RPP受控纯追踪算法
Nav2官网RPP区（https://navigation.ros.org/configuration/packages/configuring-regulated-pp.html）的算法原理论文是：Regulated Pure Pursuit for Robot Path Tracking（参见本文附件）。
-
论文说RPP会在剧烈转弯或者受限区域降低速度。（根据2.5的公式，降低速度会缩小前瞻距离）。
-
第一阶段，RPP算法会把路径点转换到机器人基准坐标下，并进行裁剪。这么做，确定路径的曲率就简化为简单的几何公式：
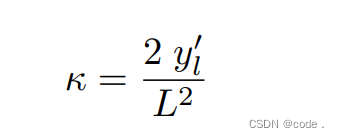
（与2.1.2最后一个公式一样，只是用的字母不同）
在转换之前要把路径中当前位置之前的所有点删掉，避免过时的路径点的转换计算量。转换后的路径中也要删除掉距离比前瞻距离大得多的点，这些点太远了在当前时刻不用考虑，但这些远处的路径点会存储起来，用作机器人沿着路径行进到后面的迭代计算，直到接受到新的路径。 -
下一步，RPP会用与APP一样的方法，如2.5的公式那样，前瞻距离 L t L_{t} Lt与速度成比例，这样在速度有较大范围变化的情况下，可以增加稳定性。前瞻距离 L t L_{t} Lt用来选择前瞻点 P l P_{l} Pl。在路径点稀疏的情况下增加插值算法，可以明显提高平滑性，但在一些（使用分辨率0.025m - 0.1 m栅格地图的）服务或者工业机器人没啥显著效果，分辨率 (0.1 - 1.0m)的稀疏路径点就有效果了。
-
通过曲率和接近试探法来计算期望的线速度，最终会取两种方法的最大值（为什么是最大值？）
-
曲率试探法（curvature heuristic 曲率启发法，曲率推导法？whatever）目的是在有剧烈转弯的地方把速度降下来。
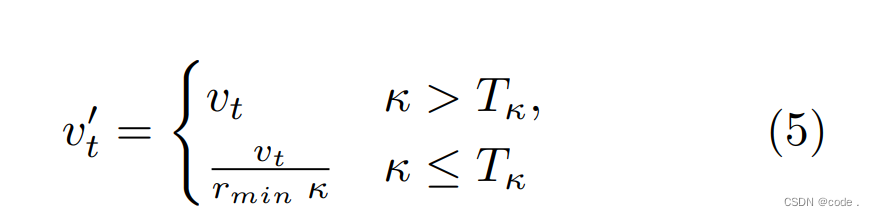
从上式可知，控制速度 v t ′ v_{t}' vt′有个最小值，就是最小速度 v t v_{t} vt。即曲率 κ \kappa κ大于某个设定值后，速度降低到一定值，不再继续下降了。
而在路径平缓，即曲率 κ \kappa κ变小的时候，速度需要比例提升，其中 r m i n r_{min} rmin是最小转弯半径。所以，在最小转弯半径的地方，曲率 κ \kappa κ<
-
最低0.47元/天 解锁文章
扫一扫
1042
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
