已知:平移向量OO’ =(a,b) ,P在O’Xθ’Yθ’坐标系下的坐标为(x1,y1), O’Xθ’Yθ’坐标系和O’X’Y’坐标系的旋转角度为θ
求:P在O’X’Y’坐标系(x1’,y1’)和OXY坐标系下的坐标(x,y)
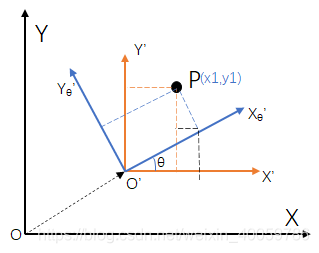

已知:平移向量OO’ =(a,b) ,P在O’Xθ’Yθ’坐标系下的坐标为(x1,y1), O’Xθ’Yθ’坐标系和O’X’Y’坐标系的旋转角度为θ
求:P在O’X’Y’坐标系(x1’,y1’)和OXY坐标系下的坐标(x,y)


 3171
3171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


