一、铺垫

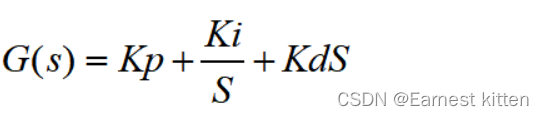 ------式1
------式1
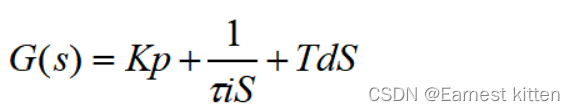 ------式2
------式2

![]()
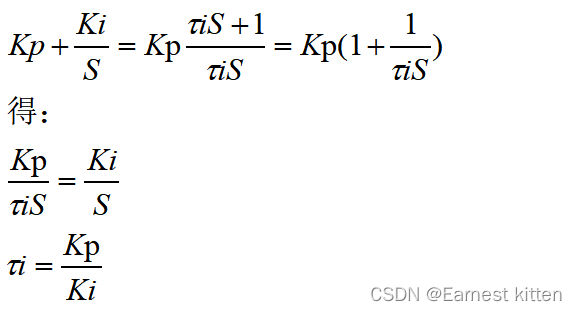 ------式3
------式3

二、公式推导
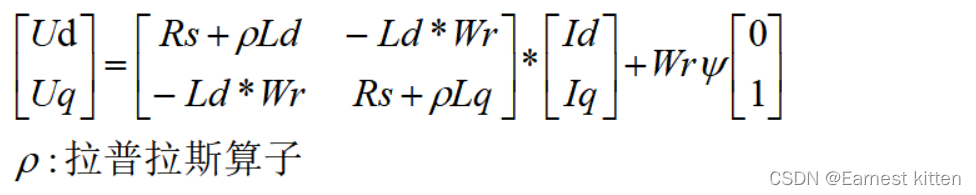 ------
式4
------
式4
接着就到了我们经常看到的旋转坐标系下的微分定子电压矩阵方程:
 ------式5
------式5
“在FOC这个规则下,能进行拉普拉斯变换的前提是“线性定长”,而上式的电压方程是一个非线性系统,并不满足比例性和叠加性原理。为了整定方便,一般将耦合项忽略掉,只看公式的前两项。”
那么由式5得到:
 ------式6
------式6
因为式6中Ud和Uq的表达形式相同,所以以其中一轴为例进行整定即可,另一轴相同。
以Q轴为例,对方程进行拉普拉斯变换得到:
![]() ------式7
------式7
由式7可以得到电机的开环传递函数,因为在电流环传递函数框图中输出为转矩iq(s),输出为Uq(s),则:
 ------式8
------式8

呼~~
接下来就引入电流环传递函数控制框图了,如下:

图1电流环传递函数框图
框图说明:
框1:为PI控制器的传递函数,和式1相同。
框2:是延时传递函数,td就是PWM周期Ts,中断读取电流值然后才能送入PI控制器得到输出电压,整个过程通常有一个周期的延迟错位。
框3:逆变器的传递函数,0.5Ts模拟PWM的小惯性特性,K认为理想型时为1
框4:电机的开环传递函数,式8已得出。
整个电流环的开环传递函数就等于四个框图传递函数的乘积。
 ------式9
------式9
将中间画红框部分以当作一个整体来化简:
 ------式10
------式10
那么可得:
 ------式11
------式11
式11中画红框的部分就是典型的I型系统了。
想用I型系统来整定,但后面化简还有一项乘积项如下:

怎么办?

还记得铺垫推出来的式3吗?
式3铺垫推出来Kp/Ki 等于积分时间常数。
先放一边。
接下来从提高系统稳定性角度考虑,可以将PI调节器零点抵消电流控制器对象传递函数的极点,抵消前,将式10代替图1中的框3和框4,调整一下框图的表达形式,例如将图1框4搞成式11,方便进行零极点对消:
 ------式11
------式11
要清楚的知道本质上没区别,纯粹的为了方便计算,可得到框图有:

图2电流环传递函数框图
图2两个画红色框图的部分分别是电流环PI调节器的零点,和控制对象的极点。
零极点对消有:
 ------式12
------式12
可得:
 ------式13
------式13
有式3和式13,所以有:
 ------式14
------式14
这个公式到这儿才清晰明了,因为式11后面的乘积项被消灭掉了,这时只保留了I型系统。

接下来就可以按照I型系统整定参数了。
三、参数整定
首先写出I型系统的开环传递函数:
 ------式15
------式15
联立式11红框部分,可得:
 ------式16
------式16
再来回顾一下这张表:

式16中的K*T对应着表1中的参数关系KT。
根据经典控制理论,二阶系统阻尼比为0.707时系统性能最佳,即KT=0.5,那么K和T的乘积为:
 ------式17
------式17
由式17和式14可得:
 ------式18
------式18
如果按照阻尼比1时,即KT=0.25,同理有:
 ------式19
------式19
整定结果如式18(不允许超调)和式19(允许超调)所示。

举个例子:
如果电流环采样频率为10KHz,即Ts=0.0001s,假设电感为0.0001H,电阻为0.05Ω,由电流环PI调节器参数计算公式得:

这个时候的带宽其实近似地认为成了:











 本文回顾了PID控制器的两种表达方式,并讨论了在电机控制中采用PI而非D参数的原因。接着推导了FOC电流环的公式,重点讲解了电流环传递函数的整定,包括I型系统的设定和阻尼比对参数的影响。最后给出了参数整定的实际示例和对知识分享的感慨。
本文回顾了PID控制器的两种表达方式,并讨论了在电机控制中采用PI而非D参数的原因。接着推导了FOC电流环的公式,重点讲解了电流环传递函数的整定,包括I型系统的设定和阻尼比对参数的影响。最后给出了参数整定的实际示例和对知识分享的感慨。
















 3724
3724

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








