目录
1.H∞输出反馈控制框架结构

被控对象状态空间一般形式:

简单叙述一下个人理解的H∞控制:对于∞范数可以理解为频域响应的最大峰值,而我们的控制就是要在控制输入u的作用下不超过给定的上界。
2.函数使用格式
关于H∞输出反馈控制器设计有两种方法:LMI方法和Riccati方法,但LMI适用性更广,分别对应MATLAB中封装的函数hinfric和hinflmi。
2.1基于Riccati方法的hinfric函数格式
gopt = hinfric(P,r) ;
[gopt,K] = hinfric(P,r);
[gopt,K,x1,x2,y1,y2,Preg] = hinfric(P,r,gmin,gmax,tol,options);其中,输入端:P为被控对象;r=[m,n],m为测量输出y的长度,n为控制输入u的长度;gmin<g<gmax,当为次优解问题时,可定义性能指标g的范围;tol为求解精度,默认为0.01;options为操作选项,一般用不上,具体可查看help文档了解;被控对象P定义格式:
P = ltisys(a,[b1 b2],[c1;c2],[d11 d12;d21 d22])函数输出端:gopt=γ为H∞的性能指标大小;K为求解的控制器;x1、x2、y1、y2用于求解黎卡提方程的解X∞ = x2/x1 and Y∞ = y2/y1;preg用于求解控制器的奇点,一般用不上。
被控对象描述方法,可以看上一篇文章:
ltisys和ltiss函数使用及示例学习_Mr. 邹的博客-CSDN博客
2.2基于LMI方法的hinflmi函数格式
gopt = hinflmi(P,r)
[gopt,K] = hinflmi(P,r)
[gopt,K,x1,x2,y1,y2] = hinflmi(P,r,g,tol,options)其中:R = x1和S = y1为LMI方程的解,g为H∞性能指标的最大值,其它含义与hinfric函数相同。
等价的LMI问题:
min γ

其中:R 和S是对称矩阵,N12和N21分别是以空间ker[B2',D12']和ker[C2, D21]中的任意一组基向量作为列向量构成的矩阵。
3.示例学习
给定一阶系统:
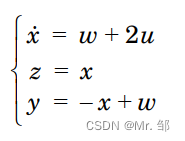
①使用ltisys函数描述连续系统:
A = 1;B1 = 1;B2 = 2;C1 = 1;D11 = 0;D12 = 0;C2 = -1;D21 = 1;D22 = 0;
B = [B1 B2];C = [C1;C2];D = [D11 D12;D21 D22];
P = ltisys(A,B,C,D);
②使用Riccati方法求解H∞分析问题:
gopt = hinfric(P,[1 1])求解结果:
![]()
③使用RLMI方法求解H∞分析问题:
gopt = hinflmi(P,[1 1])求解结果:

可见基于Riccati和LMI方法求解的结果比较接近。
④次优解H∞分析
如设定性能指标g<10,演示程序为:
[g,K,x1,x2,y1,y2] = hinfric(P,[1,1],10,10)
[g,K,x1,x2,y1,y2] = hinflmi(P,[1,1],10)⑤验证闭环系统
clsys = slft(P,K)%返回闭环系统
pole = spol(clsys)%返回闭环系统极点,验证闭环系统的稳定性
norminf(clsys);%闭环系统的RMS大小/频率响应增益峰值⑥频域分析
splot(clsys,'bo')
3.1.所有程序
A = 1;B1 = 1;B2 = 2;C1 = 1;D11 = 0;D12 = 0;C2 = -1;D21 = 1;D22 = 0;
B = [B1 B2];C = [C1;C2];D = [D11 D12;D21 D22];
P = ltisys(A,B,C,D);%开环系统
gopt = hinfric(P,[1 1])%使用Riccati方法求解H∞分析问题,并返回H∞性能指标
gopt = hinflmi(P,[1 1])%使用LMI方法求解H∞分析问题,并返回H∞性能指标
[g,K,x1,x2,y1,y2] = hinfric(P,[1,1],10,10)%使用Riccati方法求解H∞分析问题,并返回H∞性能指标和控制增益K及可行解
[g,K,x1,x2,y1,y2] = hinflmi(P,[1,1],10)%使用Riccati方法求解H∞分析问题,并返回H∞性能指标和控制增益K及可行解
clsys = slft(P,K)%返回闭环系统
pole = spol(clsys)%返回闭环系统极点,验证闭环系统的稳定性
norminf(clsys)%闭环系统的RMS大小/频率响应增益峰值
splot(clsys,'bo')4.悬架系统控制设计所需使用的函数
首先,对即将用到得一些函数做详细的说明。
4.1 ltisys函数
①作用:将状态空间实现(A, B, C, D, E)打包到一个单独的SYSTEM矩阵中
②语法:
对于传递函数:
sys = ltisys('tf',num,den)
对于连续或离散系统:
Ex' = Ax + Bu, y = Cx + Du
sys = ltisys(a)
sys = ltisys(a,e)
sys = ltisys(a,b,c)
sys = ltisys(a,b,c,d)
sys = ltisys(a,b,c,d,e)
4.2 sdiag函数
①作用:附加(连接)线性系统

②语法:
G = sdiag(g1,g2,...)
注:如果g1,g2....为传递函数,则表示的G为:

4.2.1 sdiag函数示例学习小例子
假设有一个2输入3输出得广义系统:

权矩阵w1、w2、w3(也可以当成滤波器)分别如下:

连接系统P指令为:
w1 = ltisys('tf',1,[1 0])
w3 = ltisys('tf',[100 0],[1 100])
paug = smult(p,sdiag(w1,10,w3))4.3 smult函数
①作用:串联系统

②语法:
sys = smult(g1,g2,...)
4.3.1 smult函数示例学习小例子

sys = smult(wi,g,w0)4.4 slft函数
①作用:形成两个时不变系统的线性分数阶互连(Redheffer 's star product)
②语法:
sys = slft(sys1,sys2,udim,ydim)
其中,udim、ydim分别是系统sys1的控制输入u和测量输出y的维度,如果sys2是输出反馈控制器,则udim和ydim相当于是控制器的输出和输入维度。
4.4.1 slft函数示例学习小例子

Δ、P、K均为线性时不变系统,描述从w到z得闭环系统程序为:
clsys = slft(delta,slft(p,k))
或者:
clsys = slft(slft(delta,p),k)4.5 ssub函数
①作用:在MIMO系统中选择特定的输入和输出,或者理解为选定输入到输出的子系统
②语法:
subsys = ssub(sys,inputs,outputs)
4.5.1 slft函数示例学习小例子

对于此三输入三输出的广义系统,求选择特定的u1、u3到y4、y5、y6输出的子系统,实现指令为:
subsys = ssub(p,[1,3],4:6)5 悬架系统仿真分析
5.1 悬架系统

一个车辆悬浮系统,其中 m1 表示轮胎、轮子和后轴的质量, m2表示底盘的质量, F (或 -F )是作用在底盘(或轴)上的力, b1、 是阻尼系数, b2,k1、 是弹性系数, k2 q0 表示路面的状况,这些物理参数的取值由表 4.2 给出。偏差变量 qi已被适当地放大或缩小,以使得在稳态状态下 q2 - q1 = 0 、 q1 - q0 = 0 。系统可以用以下的状态模型来表示:

5.2 仿真实现程序
% 物理参数
m1 = 1.5e3;m2 = 1e4;
k1 = 5e6;k2 = 5e5;
b1 = 1.7e3;b2 = 50e3;
%%%%%%%%广义系统描述%%%%%%
A = [0 0 1 0;0 0 0 1;-(k1+k2)/m1 k2/m1 -(b1+b2)/m1 b2/m1;k2/m2 -k2/m2 b2/m2 -b2/m2];
B = [b1/m1 0;0 0;k1/m1-(b1*(b1+b2))/(m1*m1) -1/m1;(b1*b2)/(m1*m2) 1/m2];
C1 = [1 0 0 0;0 0 0 0;k2/m2 -k2/m2 b2/m2 -b2/m2;-1 1 0 0];
D1 = [-1 0;0 1;(b1*b2)/(m1*m2) 1/m2;0 0];
C2 = [k2/m2 -k2/m2 b2/m2 -b2/m2;-1 1 0 0];
D2 = [(b1*b2)/(m1*m2) 1/m2;0 0];
sysG = ltisys(A,B,[C1;C2],[D1;D2]); %悬架系统
syswq0 = ltisys('tf',[0.01],[0.4 1]);%路面状况权矩阵传递函数Wq0 = 0.01/(0.4s+1),反映车辆匀速行驶路况
syswz1 = ltisys('tf',200,1);%被控输出权矩阵
syswz2 = ltisys('tf',0.1,1);
syswz3 = ltisys('tf',[0.0318 0.4],[0.000316 0.0314 1]);
syswz4 = ltisys('tf',100,1);
syswz5 = ltisys('tf',1,1);
syswz = sdiag(syswz1,syswz2,syswz3,syswz4,syswz5,syswz5);%添加被控输出z~权矩阵到系统
syswq = sdiag(syswq0,syswz5);%%添加路面状况权矩阵到系统
sys = smult(syswq,sysG,syswz);%广义系统
%求解H∞输出反馈控制器
[gamma,K] = hinflmi(sys,[2 1])%使用LMI方法求解,测量输出2个,控制输入1个
% [gamma,K] = hinfric(sys,[2 1])%使用黎卡提方法求解
[Ak,Bk,Ck,Dk] = ltiss(K);
%连接控制器K和路面激励下的悬架系统,即得到闭环系统
sysq0z = slft(sysG,K,1,2); % K(s)控制器 1 个输出, 2 个输入(测量输出y有2个)
%路面激励q0到各个被控变量q1-q0、F、q2''、q2-q1的传递函数
subsys1 = ssub(sysq0z,1,1);
subsys2 = ssub(sysq0z,1,2);
subsys3 = ssub(sysq0z,1,3);
subsys4 = ssub(sysq0z,1,4);
%splot(sysq0z,'st');%绘制闭环系统时域阶跃响应曲线
figure(1);splot(subsys1,'st');title('车轮动变形')
figure(2);splot(subsys2,'st');title('控制力')
figure(3);splot(subsys3,'st');title('车身加速度')
figure(4);splot(subsys4,'st');title('悬架动扰度')
% splot(sysq0z,'bo');%绘制闭环系统频域响应伯德图
figure(5);splot(subsys1,'bo');title('车轮动变形')
figure(6);splot(subsys2,'bo');title('控制力')
figure(7);splot(subsys3,'bo');title('车身加速度')
figure(8);splot(subsys4,'bo');title('悬架动扰度')
5.2.1 性能指标与控制器
gamma =
0.5628
K =
1.0e+05 *
-0.0011 0.0024 -0.0026 0.0008 0.0032 -0.0003 0.0008 -0.0005 -0.0061 0.0001
-0.0027 0.0163 -0.0208 0.0018 0.0000 -0.0030 0.0064 -0.0058 0.0461 0
-0.0196 0.1250 -0.1493 0.0068 -0.0006 -0.0161 0.0420 -0.0429 -0.0941 0
0.0341 -0.2160 0.2605 -0.0139 0.0010 0.0291 -0.0750 0.0746 0.0467 0
-0.0115 0.0727 -0.0879 0.0048 -0.0006 -0.0099 0.0254 -0.0252 -0.0073 0
-0.7013 4.4376 -5.3697 0.3040 -0.0237 -0.6085 1.5627 -1.5354 0.0135 0
1.0378 -6.5521 8.0026 -0.5223 0.0404 0.9314 -2.3942 2.2790 -3.6851 0
-0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0 0 0
0 0 0 0 0 0 0 0 0 -Inf
5.3 仿真结果分析
5.3.1 时域阶跃响应分析

图1 车身加速度阶跃响应图

图2 悬架东扰度阶跃响应图

图3 车轮动变形阶跃响应图
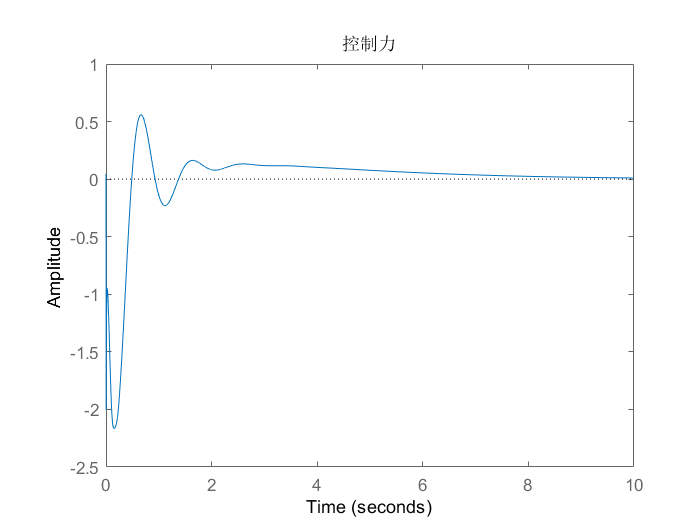
图4 控制力阶跃响应图
5.3.2 频域响应伯德图分析

图5 车身加速度频域响应伯德图

图6 悬架动扰度频域响应伯德图

图7 车轮动变形频域响应伯德图
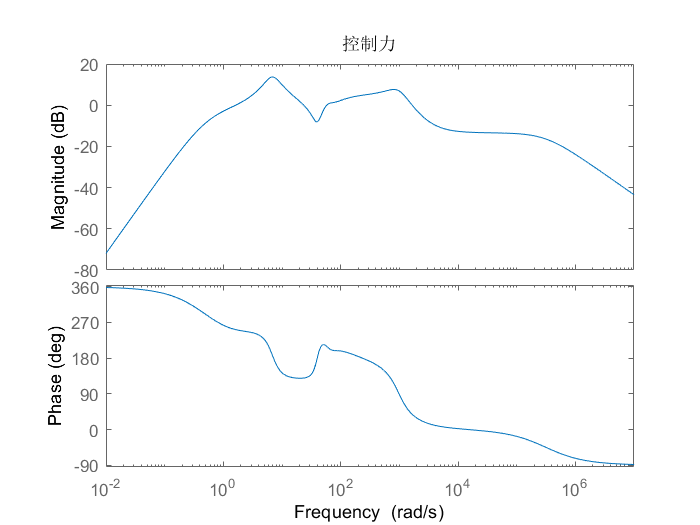
图8 控制力频域响应伯德图
6.使用hinfsys函数仿真分析
语法:
[k,g,gfin,ax,ay,hamx,hamy] =hinfsyn(p,nmeas,ncon,gmin,gmax,tol,ricmethd,epr,epp)
6.1 求解悬架控制器
% 使用hinfsyn函数求解控制器
ssG = ss(A,B,[C1;C2],[D1;D2]);
s = tf('s');
tfwz = [200 0 0 0;0 0.1 0 0;0 0 (0.0318*s+0.4)/(3.16e-4*s*s+0.0314*s+1) 0;0 0 0 100];%权矩阵
tfwq = 0.01/(0.4*s+1);
tfwz = [tfwz zeros(4,2);zeros(2,4) eye(2)];
tfwq = [tfwq 0;0 1];
ssP = tfwz*ssG*tfwq;%广义系统P
[ssK,CL,gamma] = hinfsyn(ssP,2,1)%求解控制器
step(CL)%阶跃响应图6.2 仿真结果分析

学习问题:
①这里的权矩阵如何得到的?
②车身加速度和控制输入是不是有问题?
③连接系统还是有些模糊
④控制器K的维度问题?
⑤ltiss命令在这里有什么作用?鲁棒控制理论(十六)鲁棒H∞输出反馈控制器 - 知乎
如果有帮助,麻烦帮忙点个赞是我最大的分享动力,非常感谢!
注:仅为便利自己学习,错误在所难免,如有兴趣的学者可以参考交流,谢谢!
参考资料:
《线性矩阵不等式-俞立》
《LMI Control Toolbox》





























 521
521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










