结构奇异值（SSV） µ 综合方法（不确定系统的鲁棒控制器综合）

鲁棒控制涉及：回路成形、H∞控制、结构奇异值μ综合方法。

H∞控制将H∞问题的求解简化为求解两个Riccati方程，从而传达了二次最优控制与H∞控制之间的本质联系。

µ综合是一种多变量鲁棒控制设计方法，用于设计满足多个性能要求的鲁棒控制器。在µ综合中，性能指标可以包括灵敏度、扰动响应、稳定裕度等多个方面。在设计时，需要确定权重函数或合成函数，以便将这些指标加权或组合在一起。μ 综合是有效的鲁棒控制器设计工具，它采用 D-K 迭代算法，进行结构奇异值寻优，设计保守性较低的鲁棒控制器。

为了深入了解μ综合鲁棒设计方法，需要进行以下问题的理解：

——————————————————————

（1）什么是 μ ？

A：μ是结构奇异值，鲁棒H∞性能，也称为μ， 量化了建模的不确定性如何影响反馈环路的性能。

        奇异在某些频率ω描述如何鲁棒稳定的控制器K在处理这种结构化的不确定性。这个度量是下面介绍的所谓的结构化奇异值（SSV）。

扰动块Δ对应于参数的变化，被称为“参数不确定性”。不确定块Δ不是一个完整的矩阵，而是一个对角线矩阵。它具有一定的结构，因此被称为“结构化不确定性”。

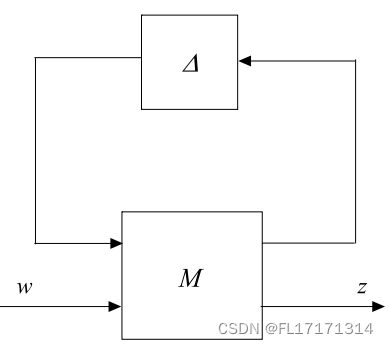
不确定性如何影响所研究的控制系统的输入/输出关系。 当M为互联传递矩阵时，关于的结构奇异值定义为

 结构奇异值的倒数表示一个与频率相关的稳定裕度。

——————————————————————————

（2）µ综合的定义？

（3）µ综合主要解决的问题？

H∞优化方法可以实现对非结构化系统扰动和标称性能要求的鲁棒稳定。通过应用适当的加权函数，可以得到一些稳健的性能要求。当使用H∞环成形设计方法。为了实现鲁棒稳定性和鲁棒性能，可以采用基于结构化奇异值μ的设计方法。

统一框架将使我们能够精确地处理具有多种不确定性来源的系统的鲁棒稳定性和鲁棒性能问题。

不确定性总是有大量的结构，然后必须用一个大的、任意的、更保守的扰动来“掩盖”，以便在参考位置保持一个简单的锥有界表示。

 

 

 

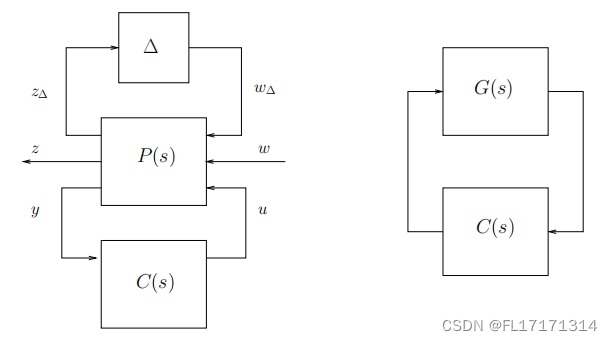
（4）µ综合的问题形成？

µ综合是一种用于控制系统鲁棒性分析和控制器设计的工具。它主要用于解决以下问题：

1. 鲁棒性分析：µ综合可以通过对控制系统中各种不确定因素的影响进行分析，来评估系统的鲁棒性。它可以帮助工程师确定系统的最小稳定性裕度，从而提高系统的可靠性。

2. 控制器设计：µ综合可以帮助工程师设计鲁棒控制器，以满足系统的性能指标和鲁棒性要求。它可以自动生成控制器，同时优化控制器参数，以提高控制系统的稳定性和性能。

3. 优化设计：µ综合可以通过优化控制器参数，使得控制系统的性能指标达到最佳状态。这可以帮助工程师提高系统的性能和可靠性，同时降低成本和复杂度。

μ综合技术扩展了H∞综合方法，设计了一种针对SISO或MIMO不确定对象的鲁棒控制器。可以使用musyn命令对具有参数不确定性、动态不确定性或两者都有的控制对象执行μ合成。

musyn使用一种称为D-K迭代的迭代过程来优化系统的鲁棒H∞性能。

musyn寻求一种最小化闭环系统鲁棒H∞性能的控制器。鲁棒H∞性能，也称为μ，量化了建模的不确定性如何影响反馈环路的性能。

鲁棒调优由PID控制器、状态空间模型和静态增益等可调组件组成的定阶或定结构控制器。

musyn使用了一个名为D-K迭代的迭代过程,以优化系统的鲁棒H∞性能。

当使用H∞环成形设计方法。为了实现鲁棒稳定性和鲁棒性能，可以采用基于结构化奇异值μ的设计方法。

两种迭代的μ-合成方法，D-K迭代和μ-K迭代方法。

系统性能规范通常可以解释为z相对于w的减少。假设w和z都是能量有界的信号，其性能要求等价于H inf从w到z的传递函数的最小化。

D-K迭代过程

使用musyn命令为不确定的控制对象设计鲁棒控制器，如使用Mu合成设计鲁棒控制器中所述。musyn使用的算法是一种称为D-K迭代的迭代过程。

（1）利用H∞综合方法找到使标称系统闭环增益最小的控制器。

（2）进行鲁棒性分析，以估计闭环系统的鲁棒H∞性能。这个量表示为一个缩放的H∞范数，涉及动态缩放，称为D和G缩放(D步骤)。

（3）找到一个新的控制器来最小化在第2步(K步)中获得的缩放H∞范数。

（4）重复步骤2和3，直到鲁棒性能停止改善。