鲁棒控制（结构奇异值（μ）综合）相关理论

鲁棒控制是控制系统设计中的一个重要概念，其主要目标是设计一个能够处理不确定性和干扰的控制器，以确保系统在各种情况下都能保持期望的性能。其中，结构奇异值（μ）综合是鲁棒控制中的一种重要方法。

结构奇异值μ理论的基本思想是将控制系统中输入、输出、传递函数、不确定性等进行回路成形，把实际控制问题归结为求结构奇异值μ的问题，从而进行控制系统的设计。μ方法的核心目的是将各种形式的不确定性整合表示为一个对角阵形式的结构，从而有效地降低鲁棒控制系统设计的保守性，并把鲁棒稳定性和鲁棒性能统一考虑。

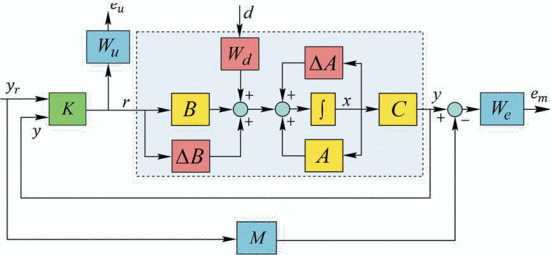
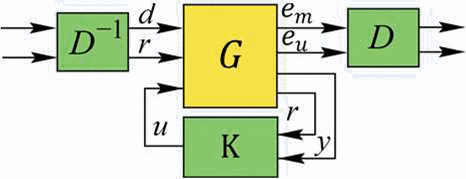
使用μ综合法首先需要将原问题重构为M-Δ结构，使之描述为线性分式的形式。在这样的增广系统结构下，用D-K迭代算法来解决μ综合问题，每一步迭代都包含一步优化和一步分析。虽然每一步是凸优化问题，但整个优化问题并不是凸的，这增加了求解的难度。

线性化模型和物理系统之间的差异和误差通过不确定性模型在控制设计中得到考虑。这些不确定性包括：未建模的高频动态、固有频率和阻尼水平的误差以及执行器和传感器误差。

干扰主要在低频处。由于测量噪声通常是高频的。

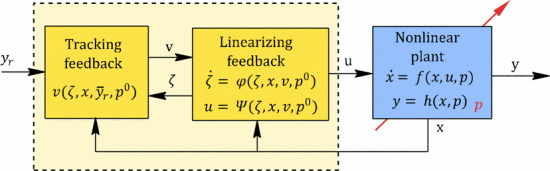
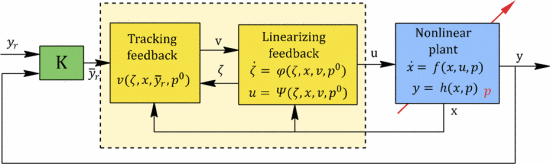
鲁棒控制器综合的目标是找到一个控制器K使得闭环系统在闭环中表现出鲁棒的稳定性和性能，尽管非线性设备的参数不确定。

DK迭代的综合框架：

参考文献：

Mu-synthesis based cascaded robust controller design for exact linearizable dynamical systems | IEEE Conference Publication | IEEE Xplorehttps://ieeexplore.ieee.org/abstract/document/9528491