本教程相关代码已经上传至 https://github.com/iMetaScience/iMetaPlot/tree/main/230107FacetsBoxplot 如果你使用本代码,请引用:Yu-Xi Zhu. 2022. Gut microbiota composition in the sympatric and diet-sharing Drosophila simulans and Dicranocephalus wallichii bowringi shaped largely by community assembly processes rather than regional species pool. iMeta 1: e57. https://doi.org/10.1002/imt2.57
代码编写及注释:农心生信工作室
写在前面
箱线图 (boxplot) 是一种基于五位数摘要(“最小”,第一四分位数(Q1),中位数,第三四分位数(Q3)和“最大”)显示数据分布的标准化方法, 可以表示微生物群落的alpha多样性。本期我们挑选2022年10月13日刊登在iMeta上的Gut microbiota composition in the sympatric and diet-sharing Drosophila simulans and Dicranocephalus wallichii bowringi shaped largely by community assembly processes rather than regional species pool - iMeta | 扬州大学杜予州团队揭示同域内同食物的两种昆虫肠道微生物群落装配机制,选择文章的Figure 1A进行复现,基于vegan包和ggplot2包,讲解和探讨alpha多样性的计算、箱线图的可视化以及用ANOVA进行差异分析并用字母标注显著性,先上原图:

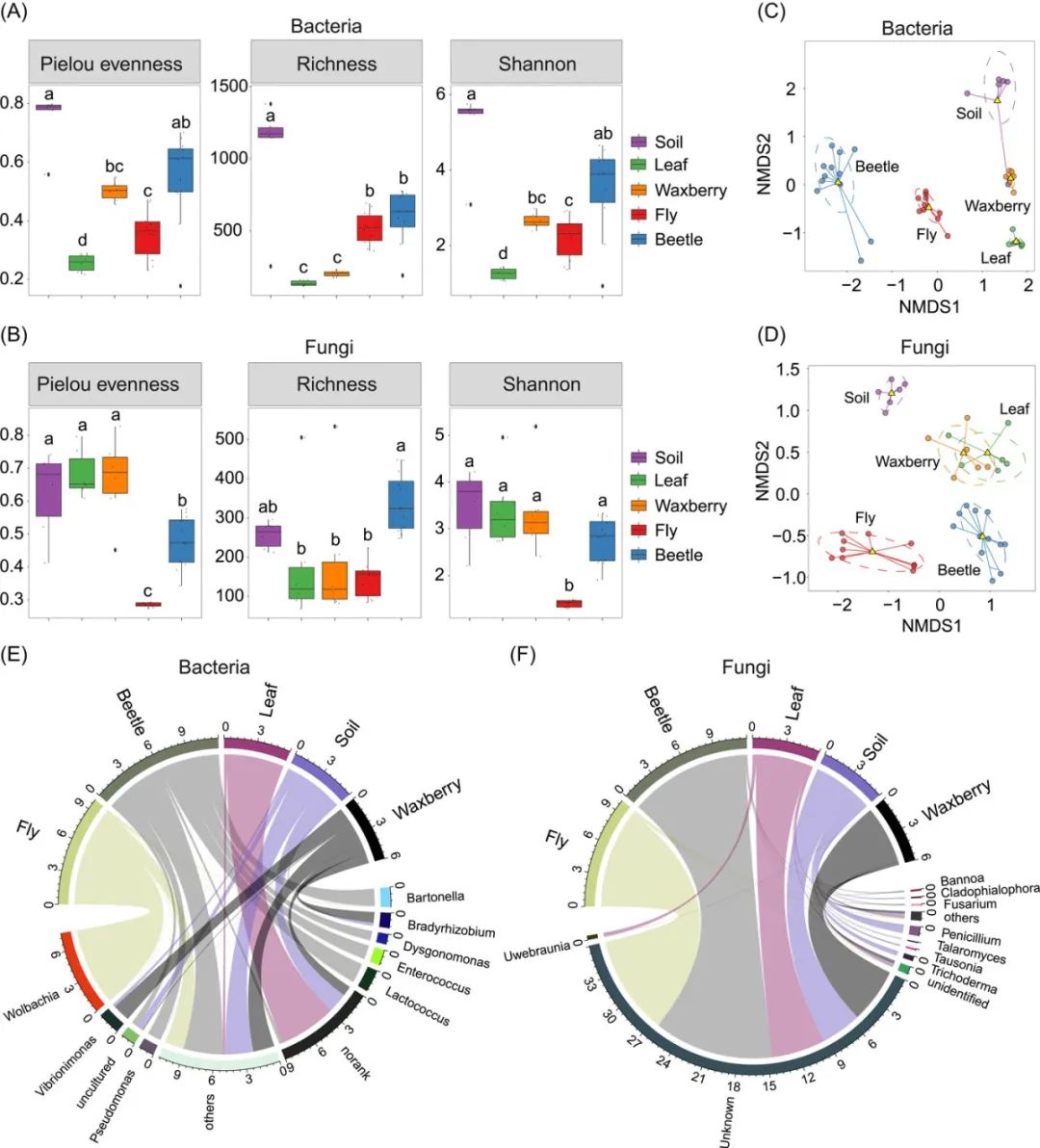
接下来,我们将通过详尽的代码逐步拆解原图,最终实现对原图的复现。
R包检测和安装
01
安装核心R包vegan、ggplot2以及一些功能辅助性R包,并载入所有R包。
# 下载包
if (!require("vegan"))
install.packages('vegan')
if (!require("ggplot2"))
install.packages('ggplot2')
if (!require("tidyverse"))
install.packages('tidyverse')
if (!require("agricolae"))
install.packages('agricolae')
# 加载包
library(vegan)
library(ggplot2)
library(tidyverse)
library(agricolae)生成测试数据
02
由于缺少原始数据,因此本例使用vegan包自带的dune数据集进行测试。dune数据集的格式是otu表转置后的格式,包含了20个样品,每个样品有30个物种丰度,每一行是一个样品,每一列是一个物种。
# 载入dune数据集
data(dune)
#载入dune包含分组信息等的元数据(即metadata),分组信息为Management列
data(dune.env)03
计算alpha多样性,包括均匀度、丰富度和香农指数。
#计算丰富度richness,即群落中丰度大于0的otu数量之和
richness <- rowSums(dune>0)
#计算香农指数Shannon diversity index,以e作为底数
shannon <- diversity(dune, index = 'shannon', base = exp(1))
#计算均匀度Pielou evenness,即香农指数与ln(Richness)的比值
pielo <- shannon/log(richness, base = exp(1))04
创建函数一步计算alpha多样性。
calculate_alpha <- function(otu){
data_richness <- rowSums(otu>0)
data_shannon <- diversity(otu, index = 'shannon', base = exp(1))
data_pielou <- data_shannon/log(data_richness, base = exp(1))
alpha_matrix <- cbind(data_pielou, data_richness, data_shannon)
alpha_df <- as.data.frame(alpha_matrix)
return(alpha_df)
}05
利用函数calculate_alpha(),创建绘图所需数据框并重命名其中的列:
plot_df <- calculate_alpha(dune)%>%
cbind(dune.env$Management)%>%
rename_with(~"Group", 4)作图预览
06
接下来,逐一预览不同alpha多样性的箱线图:
#绘制Pielou evenness的箱线图
p_pielou <- ggplot(plot_df, aes(Group, data_pielou))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group, data_pielou), size = 0.8) #添加散点
#绘制Shannon的箱线图
p_richness <- ggplot(plot_df, aes(Group, data_richness))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group, data_richness), size = 0.8)
#绘制Richness的箱线图
p_shannon <- ggplot(plot_df, aes(Group, data_shannon))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group, data_shannon), size = 0.8)
07
现在,需要绘制分面箱线图,以在同一张图片中表示三种不同的alpha多样性,为此,我们需要将plot_df的宽表转化为长表:
#宽表转化为长表
df_long <- pivot_longer(plot_df, cols = -Group, names_to = "type", values_to = "alpha_index")
#根据不同的alpha多样性绘制分面箱线图
p <- ggplot(df_long, aes(Group, alpha_index))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group, alpha_index), size = 0.8)+
facet_wrap(.~type, #type列作为变量,分面为一行多列
scales = "free_y")+ #scales = "free_y"可以使各个分面有自己的y轴刻度
theme(panel.grid = element_blank(),
panel.background = element_rect(fill = 'white'),
panel.border = element_rect(fill = NA, color = "black", size = 0.5, linetype = "solid"),
axis.title = element_blank(),
axis.text.x = element_blank())
08
到这一步,基本的分面箱线图已经完成,但我们注意到原图做了差异分析,并用字母标记了差异分析结果。这里我们以参数检验中的one-way ANOVA为例进行差异分析(默认总体符合正态分布和方差齐性,所以在这里没有做正态检验和方差齐性检验):
#先选择Shannon进行one-way ANOVA分析
shannon_anova <- aov(data_shannon~Group, data = plot_df)
#查看ANOVA结果,其中Pr(>F)是p值,p<0.05时,认为不同组的Shannon具有显著差异
summary(shannon_anova)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Group 3 0.7171 0.23905 5.676 0.00763 **
#> Residuals 16 0.6739 0.04212
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#进一步得到更详细的两两比较,用TukeyHSD()函数
pair_comparison <- TukeyHSD(shannon_anova)
pair_comparison <- as.data.frame(pair_comparison$Group)
pair_comparison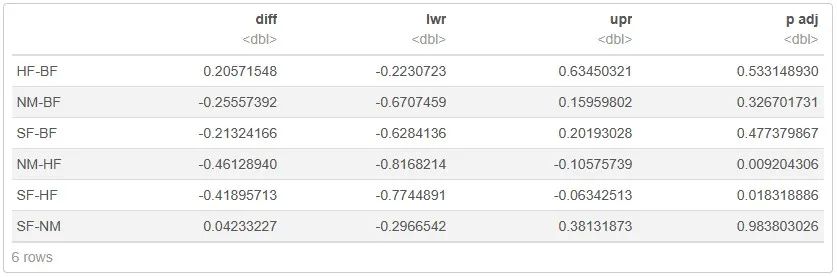
09
如何用abc字母标注差异分析的结果,是本文的难点。为此,我们利用agricolae包的orderPvalue()函数来得到显著性标记。这个函数需要四个参数,因此要对数据提前处理:
#计算分组平均数
group_mean <- aggregate(x = plot_df$data_shannon, by = list(plot_df$Group), FUN = mean)%>%
rename_with(~c("Group", "mean_val"), 1:2)
#创建一个pvalue矩阵
ntr <- nrow(group_mean)
mat <- matrix(1, ncol = ntr, nrow = ntr)
p <- pair_comparison$`p adj`
k <- 0
for (i in 1:(ntr - 1)) {
for (j in (i + 1):ntr) {
k <- k + 1
mat[i, j] <- p[k]
mat[j, i] <- p[k]
}
}
treatments <- as.vector(group_mean$Group)
means <- as.vector(group_mean$mean_val)
alpha <- 0.05
pvalue <- mat
out <- orderPvalue(treatments, means, alpha, pvalue, console = TRUE)
out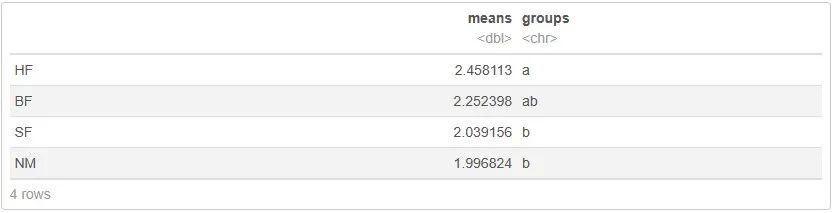
10
将整个ANOVA分析和显著性标记过程打包成一个函数anova_sig()便于后续绘图,在这个函数里我们还添加了分组最大值和sd值的计算:
anova_sig <- function(df, alpha_diversity, group){
anova <- aov(alpha_diversity~group, data = plot_df)
pair_comparison <- TukeyHSD(anova)
pair_comparison_df <- pair_comparison$group
pair_comparison_df <- as.data.frame(pair_comparison_df)
group_mean <- aggregate(x = alpha_diversity, by = list(group), FUN = mean)%>%
rename_with(~c("Group", "mean_val"), 1:2)
group_max <- aggregate(x = alpha_diversity, by = list(group), FUN = max)%>%
rename_with(~c("Group", "max"), 1:2)
group_sd <- aggregate(x = alpha_diversity, by = list(group), FUN = sd)%>%
rename_with(~c("Group", "sd"), 1:2)
ntr <- nrow(group_mean)
mat <- matrix(1, ncol = ntr, nrow = ntr)
p <- pair_comparison_df$`p adj`
k <- 0
for (i in 1:(ntr - 1)) {
for (j in (i + 1):ntr) {
k <- k + 1
mat[i, j] <- p[k]
mat[j, i] <- p[k]
}
}
treatments <- as.vector(group_mean$Group)
means <- as.vector(group_mean$mean_val)
alpha <- 0.05
pvalue <- mat
output <- orderPvalue(treatments, means, alpha, pvalue, console = TRUE)
output$Group <- rownames(output)
output <- left_join(output, group_max, by = "Group")
output <- left_join(output, group_sd, by = "Group")
return(output)
}
#丰富度的ANOVA检验及结果
data_richness <- plot_df$data_richness
Group = plot_df$Group
richness_out <- anova_sig(plot_df, data_richness, Group)
richness_out$type <- "data_richness" #添加一列alpha多样性类别
#均匀度的ANOVA检验及结果
data_pielou <- plot_df$data_pielou
Group = plot_df$Group
pielou_out <- anova_sig(plot_df, data_pielou, Group)
pielou_out$type <- "data_pielou"
#香农指数的的ANOVA检验及结果
data_shannon <- plot_df$data_shannon
Group = plot_df$Group
shannon_out <- anova_sig(plot_df, data_shannon, Group)
shannon_out$type <- "data_shannon"
#合并三者结果
alpha_out <- rbind(pielou_out, shannon_out, richness_out)%>%rename_with(~"marker", 2)
#将长表与差异分析结果合并
df_long_all <- left_join(df_long, alpha_out, by = c("type", "Group"))11
最后,用geom_text()来添加abc标记,成品图可以根据个人喜好用AI微调:
p <- ggplot(df_long_all, aes(Group, alpha_index))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group, alpha_index), size = 0.8)+
geom_text(aes(x = Group, y = max+sd, label = marker), size = 4, position = position_dodge(0.6))+
facet_wrap(.~type, #type列作为变量,分面为一行多列
scales = "free_y")+ #scales = "free_y"可以使各个分面有自己的y轴刻度
theme(panel.grid = element_blank(),
panel.background = element_rect(fill = 'white'),
panel.border = element_rect(fill = NA, color = "black", size = 0.8, linetype = "solid"),
axis.title = element_blank(),
axis.text.x = element_blank())
完整代码
# 下载包
if (!require("vegan"))
install.packages('vegan')
if (!require("ggplot2"))
install.packages('ggplot2')
if (!require("tidyverse"))
install.packages('tidyverse')
if (!require("agricolae"))
install.packages('agricolae')
# 加载包
library(vegan)
library(ggplot2)
library(tidyverse)
library(agricolae)
# 载入dune数据集
data(dune)
#载入dune包含分组信息等的元数据(即metadata),分组信息为Management列
data(dune.env)
#计算丰富度Richness,即群落中丰度大于0的otu数量之和
richness <- rowSums(dune>0)
#计算香农指数Shannon diversity index,以e作为底数
shannon <- diversity(dune , index = 'shannon' , base = exp(1))
#计算均匀度Pielou evenness,即香农指数与ln(Richness)的比值
pielo <- shannon/log(richness , base = exp(1))
#创建函数一步计算alpha多样性
calculate_alpha <- function(otu){
data_richness <- rowSums(otu>0)
data_shannon <- diversity(otu , index = 'shannon' , base = exp(1))
data_pielou <- data_shannon/log(data_richness , base = exp(1))
alpha_matrix <- cbind(data_pielou , data_richness , data_shannon)
alpha_df <- as.data.frame(alpha_matrix)
return(alpha_df)
}
plot_df <- calculate_alpha(dune)%>%
cbind(dune.env$Management)%>%
rename_with(~"Group" , 4)
#绘制Pielou evenness的箱线图
p_pielou <- ggplot(plot_df , aes(Group , data_pielou))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group , data_pielou) , size = 0.8) #添加散点
#绘制Shannon的箱线图
p_richness <- ggplot(plot_df , aes(Group , data_richness))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group , data_richness) , size = 0.8)
#绘制Richness的箱线图
p_shannon <- ggplot(plot_df , aes(Group , data_shannon))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group , data_shannon) , size = 0.8)
#宽表转化为长表
df_long <- pivot_longer(plot_df , cols = -Group , names_to = "type" , values_to = "alpha_index")
#根据不同的alpha多样性绘制分面箱线图
p <- ggplot(df_long , aes(Group , alpha_index))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group , alpha_index) , size = 0.8)+
facet_wrap(.~type , #type列作为变量,分面为一行多列
scales = "free_y")+ #scales = "free_y"可以使各个分面有自己的y轴刻度
theme(panel.grid = element_blank() ,
panel.background = element_rect(fill = 'white') ,
panel.border = element_rect(fill = NA , color = "black" , size = 0.5 , linetype = "solid") ,
axis.title = element_blank() ,
axis.text.x = element_blank())
#先选择Shannon进行one-way ANOVA分析
shannon_anova <- aov(data_shannon~Group , data = plot_df)
#查看ANOVA结果,其中Pr(>F)是p值,p<0.05时,认为不同组的Shannon具有显著差异
summary(shannon_anova)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Group 3 0.7171 0.23905 5.676 0.00763 **
#> Residuals 16 0.6739 0.04212
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#进一步得到更详细的两两比较,用TukeyHSD()函数
pair_comparison <- TukeyHSD(shannon_anova)
pair_comparison <- as.data.frame(pair_comparison$Group)
#计算分组平均数
group_mean <- aggregate(x = plot_df$data_shannon , by = list(plot_df$Group) , FUN = mean)%>%
rename_with(~c("Group" , "mean_val") , 1:2)
#创建一个pvalue矩阵
ntr <- nrow(group_mean)
mat <- matrix(1 , ncol = ntr , nrow = ntr)
p <- pair_comparison$`p adj`
k <- 0
for (i in 1:(ntr - 1)) {
for (j in (i + 1):ntr) {
k <- k + 1
mat[i , j] <- p[k]
mat[j , i] <- p[k]
}
}
treatments <- as.vector(group_mean$Group)
means <- as.vector(group_mean$mean_val)
alpha <- 0.05
pvalue <- mat
out <- orderPvalue(treatments , means , alpha , pvalue , console = TRUE)
anova_sig <- function(df , alpha_diversity , group){
anova <- aov(alpha_diversity~group , data = plot_df)
pair_comparison <- TukeyHSD(anova)
pair_comparison_df <- pair_comparison$group
pair_comparison_df <- as.data.frame(pair_comparison_df)
group_mean <- aggregate(x = alpha_diversity , by = list(group) , FUN = mean)%>%
rename_with(~c("Group" , "mean_val") , 1:2)
group_max <- aggregate(x = alpha_diversity , by = list(group) , FUN = max)%>%
rename_with(~c("Group" , "max") , 1:2)
group_sd <- aggregate(x = alpha_diversity , by = list(group) , FUN = sd)%>%
rename_with(~c("Group" , "sd") , 1:2)
ntr <- nrow(group_mean)
mat <- matrix(1 , ncol = ntr , nrow = ntr)
p <- pair_comparison_df$`p adj`
k <- 0
for (i in 1:(ntr - 1)) {
for (j in (i + 1):ntr) {
k <- k + 1
mat[i , j] <- p[k]
mat[j , i] <- p[k]
}
}
treatments <- as.vector(group_mean$Group)
means <- as.vector(group_mean$mean_val)
alpha <- 0.05
pvalue <- mat
output <- orderPvalue(treatments , means , alpha , pvalue , console = TRUE)
output$Group <- rownames(output)
output <- left_join(output , group_max , by = "Group")
output <- left_join(output , group_sd , by = "Group")
return(output)
}
#丰富度的ANOVA检验及结果
data_richness <- plot_df$data_richness
Group = plot_df$Group
richness_out <- anova_sig(plot_df , data_richness , Group)
richness_out$type <- "data_richness" #添加一列alpha多样性类别
#均匀度的ANOVA检验及结果
data_pielou <- plot_df$data_pielou
Group = plot_df$Group
pielou_out <- anova_sig(plot_df , data_pielou , Group)
pielou_out$type <- "data_pielou"
#香农指数的的ANOVA检验及结果
data_shannon <- plot_df$data_shannon
Group = plot_df$Group
shannon_out <- anova_sig(plot_df , data_shannon , Group)
shannon_out$type <- "data_shannon"
#合并三者结果
alpha_out <- rbind(pielou_out , shannon_out , richness_out)%>%rename_with(~"marker" , 2)
#将长表与差异分析结果合并
df_long_all <- left_join(df_long , alpha_out , by = c("type" , "Group"))
pdf("Figure 1A.pdf" , width = 8 , height = 6)
ggplot(df_long_all , aes(Group , alpha_index))+
geom_boxplot(aes(fill = Group))+
geom_jitter(aes(Group , alpha_index) , size = 0.8)+
geom_text(aes(x = Group , y = max+sd , label = marker) , size = 4 , position = position_dodge(0.6))+
facet_wrap(.~type , #type列作为变量,分面为一行多列
scales = "free_y")+ #scales = "free_y"可以使各个分面有自己的y轴刻度
theme(panel.grid = element_blank() ,
panel.background = element_rect(fill = 'white') ,
panel.border = element_rect(fill = NA , color = "black" , size = 0.8 , linetype = "solid") ,
axis.title = element_blank() ,
axis.text.x = element_blank())
dev.off()以上数据和代码仅供大家参考,如有不完善之处,欢迎大家指正!
更多推荐
(▼ 点击跳转)
iMeta | 德国国家肿瘤中心顾祖光发表复杂热图(ComplexHeatmap)可视化方法
iMeta | 浙大倪艳组MetOrigin实现代谢物溯源和肠道微生物组与代谢组整合分析
第1卷第1期
第1卷第2期
第1卷第3期
第1卷第4期
期刊简介
“iMeta” 是由威立、肠菌分会和本领域数百位华人科学家合作出版的开放获取期刊,主编由中科院微生物所刘双江研究员和荷兰格罗宁根大学傅静远教授担任。目的是发表原创研究、方法和综述以促进宏基因组学、微生物组和生物信息学发展。目标是发表前10%(IF > 15)的高影响力论文。期刊特色包括视频投稿、可重复分析、图片打磨、青年编委、前3年免出版费、50万用户的社交媒体宣传等。2022年2月正式创刊发行!
联系我们
iMeta主页:http://www.imeta.science
出版社:https://onlinelibrary.wiley.com/journal/2770596x
投稿:https://mc.manuscriptcentral.com/imeta
邮箱:office@imeta.science






























 178
178

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








