【控制理论】干扰观测控制读书笔记（Disturbance Observer-Based on control)

对于高精度的控制要求，必然要考虑干扰对系统的影响，简单介绍一下干扰抑制的背景和控制方法。
一、背景
为了更清晰地分析，看到控制的本质，从最简单的一阶惯性环节对象分析起， 系统的状态方程为：

假设期望输出yr是常数，dyr=0,且定义则有

1、高增益控制
控制器设计为，将控制率带入系统状态方程，有，一阶常系数非奇异微分方程求解，得到

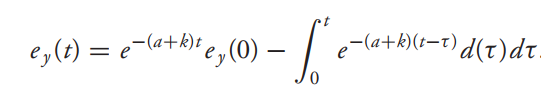
用控制框图表示一下，更加清晰一点：

如果干扰是有界的，满足，那么有：

则当t趋于无穷大时，稳态误差也是一个有界的值。，增益k越大，误差也就越小。

考虑最一般的情况，如果干扰d是一个常值干扰，则，考虑趋于无穷时刻的偏差，有

可见对于最简单的一阶惯性环节，在干扰存在时，这种方法无法消除干扰带来的稳态误差，而且为了使得误差尽可能小，需要取高增益控制率以抑制扰动的影响。

2、积分控制

积分项可以消除稳态误差，如果考虑带有积分项的控制率，带入状态方程有

化为状态空间形式，，，

从公式可以看出，当干扰为常值干扰时，干扰项的导数为零，且A矩阵是Hurwitz的，此时系统渐进稳定，无穷时刻的偏差为零。

Hurwitz矩阵：矩阵特征值实部都小于零的矩阵，如果系统矩阵是Hurwitz的，那么系统渐进稳定。

考虑如果干扰的导数非零，但是其有界的情况：

最终有，

从以上的分析可以知道，积分控制能消除常值干扰，但是对于变化的干扰稳态误差依然存在。

 

3、滑模控制

之前写了一篇文章详细讨论了滑模控制器的实现和分析过程，https://blog.csdn.net/xiaohejiaoyiya/article/details/90271529，这里就不再重复分析了。那个例子是考虑一个简单的双积分器对象，

先设计一个可以让状态渐进稳定的滑模面，然后基于此设计控制率让状态达到滑模面上。

这里只把滑模控制器的控制率写一下：

，

以上几种控制器都是用高增益的方式来抑制干扰，如果干扰有界，或者干扰的变化有界，那么我用比你干扰最大值的控制能量来压制，简单来讲就是比你快，还比你强，那么不管你干扰是怎样的形式，都翻不起多大风浪，系统是稳定的。

除了以上介绍了三种，H无穷、鲁棒控制也是同样的思路。这种控制方式简单粗放有误差但是很有效，下面另一种基于补偿的控制策略，也就是基于干扰观测器的控制方式。

 

二、基于干扰观测器的控制

基本思路是先构造干扰观测器将干扰量测出来，用估计干扰补偿实际干扰，如果模型估计得很准确（很难很难），那么系统将简化成一个不受干扰影响的纯净系统，再在这基础上设计反馈控制器就比较简单了。

 

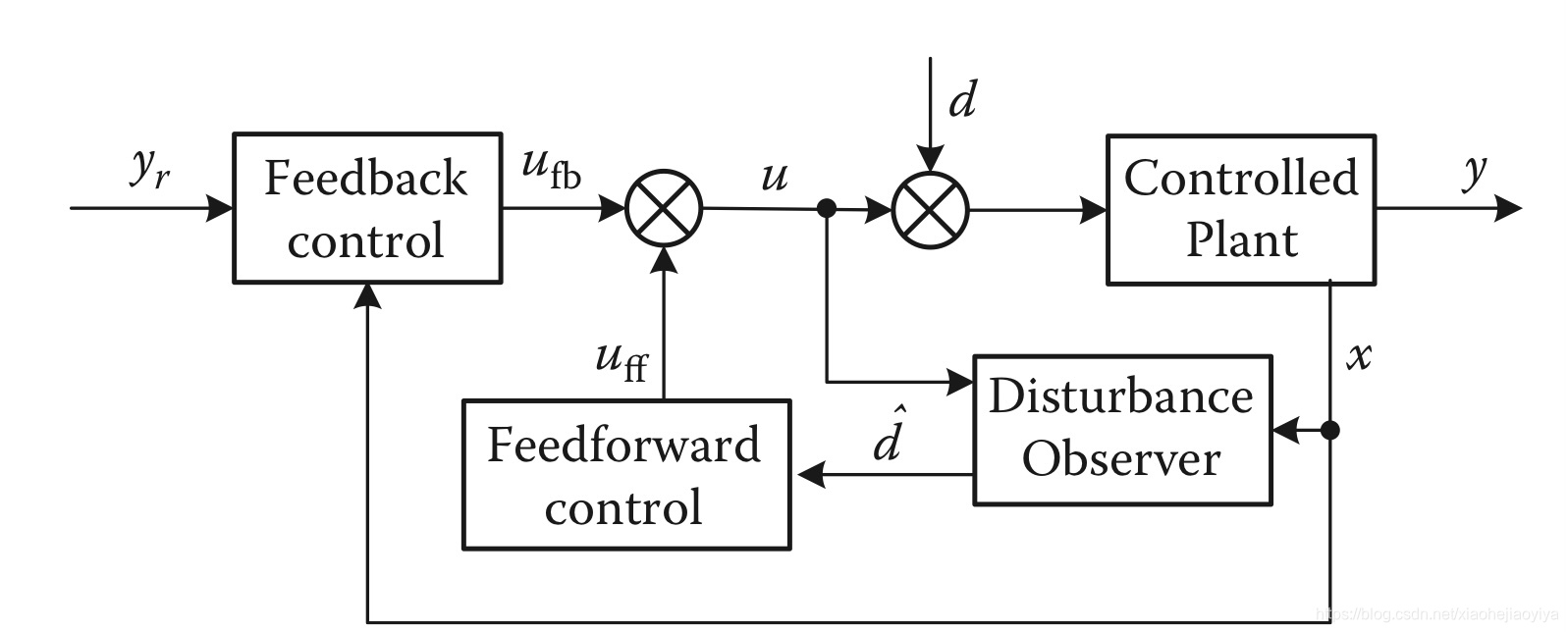
1、DOB

对于一个系统：

，假设无穷时间后干扰会收敛到一个常值，,

若设计如下的DOB干扰观测器

则估计干扰和实际干扰之间的偏差值为：

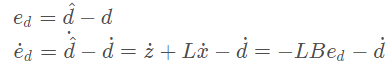
如果矩阵-LB是赫尔维兹矩阵，那么最终估计干扰值会收敛到实际干扰值，此时只需要设计控制器,带入系统方程

如果（A+BK）是Hurwitz的，那么系统稳定

控制框图如下：

 

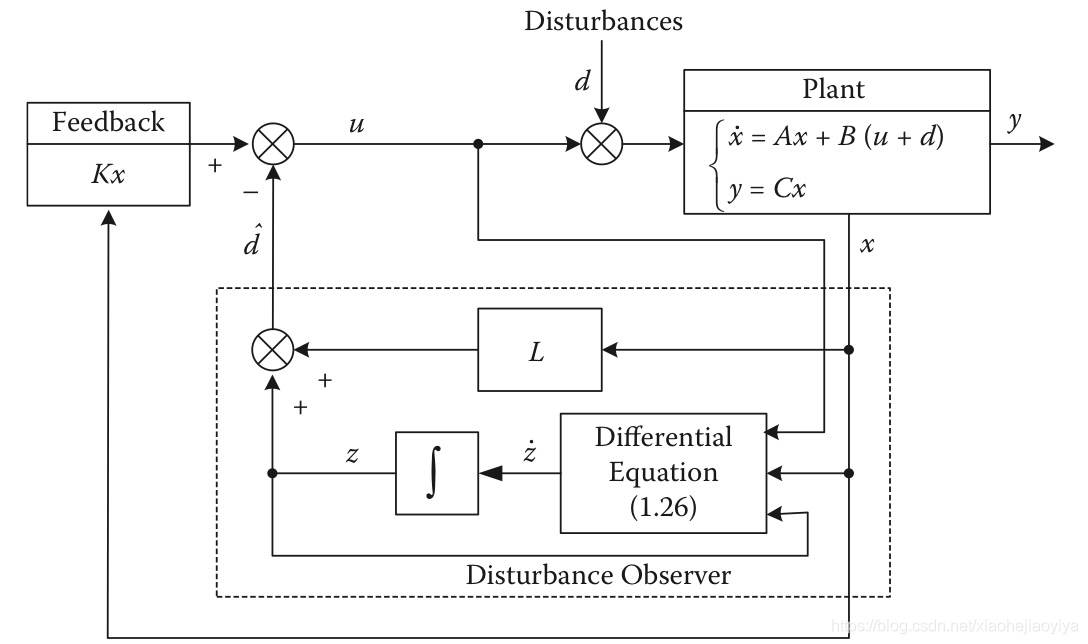
2、ESO（Extended State Observer)

ESO是韩京清老师提出的一类干扰估计方法， 常常和跟踪微分器、非线性PID组合在一起构成自抗扰控制器（ADRC控制）。

把一般系统的状态方程逐个写出来：

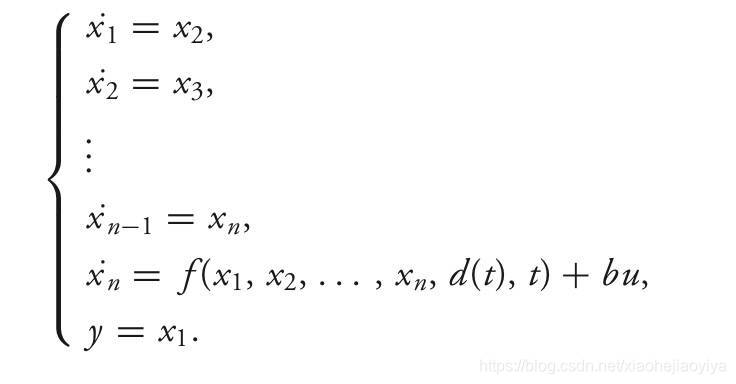
如果把包括系统动态、模型不确定性、外部扰动统一用一个新的状态来表示，那么有扩张之后的状态方程：

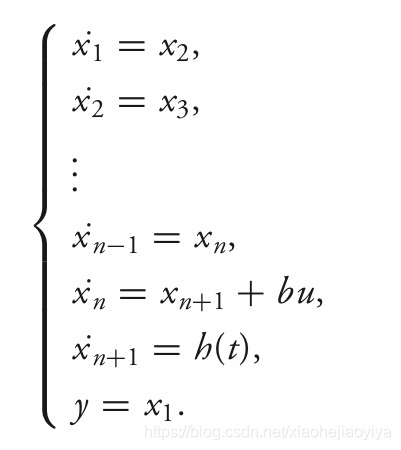
设计状态观测器使得zi跟踪xi，i=[1,n+1]

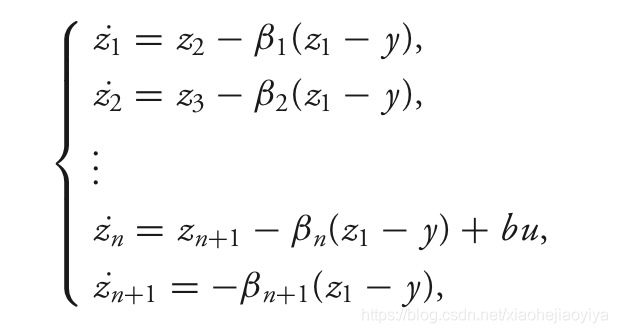
观察干扰收敛的情况：

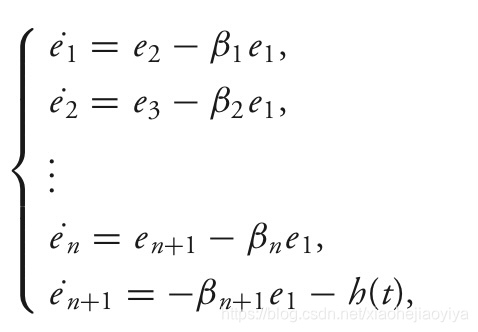
写成状态空间形式：

和【2积分控制】中分析的类似，设计使得矩阵是Hurwitz的，且h(t)有界，那么误差状态将收敛到零， 估计干扰将收敛到实际干扰。

将干扰补偿后，再根据相应的性能指标设计反馈控制器。

 

基于干扰观测器的补偿控制能施加更精准的控制，从能量输出角度讲它也更加经济。但是这种方法对模型的要求要更高，通常需要花很多工夫在辨识上。

如果模型不太准确，有可能干扰的补偿没起到作用，反而还产生了更坏的影响。

本博客是阅读李世华老师专著《Disturbance Observer-Based on control》的笔记