点云配准--4PCS原理与应用

总结：4PCS不同于icp和ndt，其是一种基于局部特征（特征描述子）的全局配准方法，对于噪点和异常值、低重叠度具有稳健性，对于配准初值不敏感。

1预备知识

1.0 wide base

4pcs算法的关键是选取一个宽基集（wide-base），如图。（就是选取的点的距离相对大些，算法才更稳定，明显上面的配准效果比下面的好，因为上面的点隔得远，但是最远距离要受重叠度的限制）。1

1.1 LCP(largest common pointset)

即通过一个刚体变换，使得重叠区域内所有点对之间的距离小于δ，这个重叠区域就是要求的最大公共点集.
简单来说就是，给定两个处于任意初始位置的点集P和Q，找到两个点集之间的最佳刚性变换，使得P，Q中两点间距离小于δ的点数最多.
$\delta$为常数，$T$变换矩阵，$P_{\max }\subseteq P，$ 满足 $\forall P_i\in P_{\max },\Vert \overrightarrow{T\left(p_i\right)}-\overrightarrow{q_i}\Vert \le \delta$都成立，则满足最多数量的那个$P_{MAX}$称为最大公共集 (largest common pointset LCP)2
即可以利用LCP做为代价函数，求解变换矩阵,4pcs就是利用LCP做为求解变换矩阵的度量。
wide-base和LCP度量的组合使得4PCS配准方法能应对噪点和异常值

1.2 RANSAC配准过程

基于RANSAC的对齐过程很简单：从P中随机选择三个不同的点，从Q中随机选择三个不同的点，形成对应的一对基，计算对齐基对的候选变换Ti，然后计算距离Q中点δ-距离内的P中的点ki的数量。如果ki足够大，则接受Ti作为一个好的解决方案。否则，通过随机选择另一个三个点来重复该过程，从而导出可能改进当前最佳拟合的不同候选变换。

1.3 Randomized Alignment

该配准方法是RANSAC算法的一种变体。该过程从P中随机选取一个基，计算将该基与Q中所有可能的基对齐的变换，并验证配准结果。如在RANSAC中一样，为了获得一定的成功概率，该方法重复从P中选择L个不同的基。此外，验证阶段也是随机化的：首先，只验证P中数量恒定的随机点，并且仅当该子集的显著部分匹配良好时，才测试其余点。
$p_g$是从点云$P$中随机选择一点，该点恰好也出现在点云$Q$中的概率，（即该点在重叠区域内）。用于配准的基（base）的数量为$N$。$p_f$是在尝试L次后找不到存在的良好拟合时，算法退出的概率。因为我们从$P$中随机选择基，假设： $p_f={\left(1-p_g^N\right)}^L$，设$p_s$为配准成功的概率，则有迭代次数$L$：

$$L>\log \left(1-p_s\right)/\log \left(1-p_g^N\right)\text{\hspace{1em}(1)}$$

For rigid transforms, it is sufficient to have $N=3$

4PCS算法流程是基于Randomized Alignment方法。然而，文中引入了平面全等集的思想，从Q中只选择一小部分可能与P中给定的基相匹配的基，而不是从Q中测试所有可能的基.

2 Approximate Congruent 4-Points近似共面四点（4PCS特征）

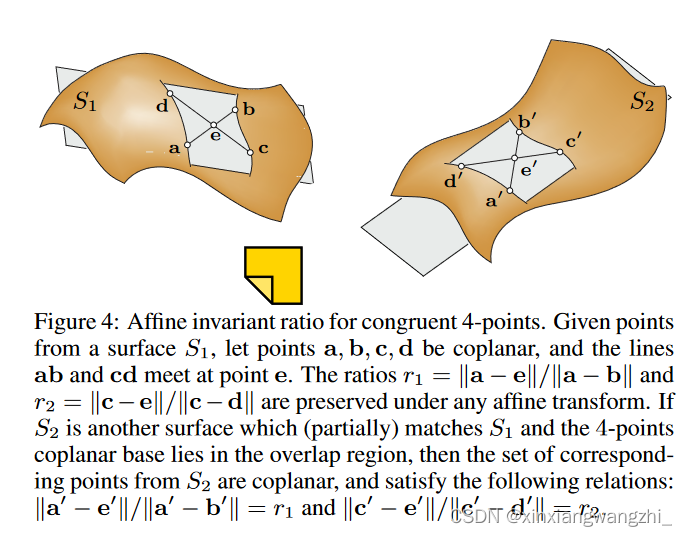
仿射变换具有以下性质：给定三个共线点{a，b，c}，比率‖a− $\Vert \mathbf{a}-\mathbf{b}\Vert /\Vert \mathbf{a}-\mathbf{c}\Vert$是不变的。Huttenlocher[1991]使用该不变量提取平面上4个点的所有二维仿射不变量集，这些不变量在仿射变换下是等价的。我们在三维空间中采用类似的方法。给定一个共面4点基，在另外一个点云数据中寻找其仿射等价（全等）4点集。所有仿射不变4点集是3维空间中4点全等点的超集。随后，我们验证这样的4点集是否（近似）与所选的基集一致。首先简要介绍了二维仿射不变四点集的提取方法，然后详细介绍了三维仿射不变四点集的提取过程。

2.1 4点对的仿射不变性

Huttenlocher（1991）介绍了一种提取二维仿射不变的4点集的方法。设一组共面点X≡ {a，b，c，d}，非所有点共线，定义了三个共线点的两个独立比率。设ab和cd为相交于点e的两条线。这两个比率$r_1,r_2$：
$$\begin{gathered} r_1=\Vert \mathbf{a}-\mathbf{e}\Vert /\Vert \mathbf{a}-\mathbf{b}\Vert \\ {r}_2=\Vert \mathbf{c}-\mathbf{e}\Vert /\Vert \mathbf{c}-\mathbf{d}\Vert \end{gathered}$$
这两个比率$r_1,r_2$,具有仿射变换不变性，并且能唯一定义四个点。
如下图：

现在，给定一个由n个点组成的集Q，以及两个仿射不变比r1和r2，我们可以有效地提取由这两个不变量定义的所有4个点集，其中k是4个点集的数目，如下所示：对于每对点q1，q2∈ Q、 计算两个中间点：
$${\mathbf{e}}_1={\mathbf{q}}_1+r_1\left({\mathbf{q}}_2-{\mathbf{q}}_1\right)$$
$${\mathbf{e}}_2={\mathbf{q}}_1+r_2\left({\mathbf{q}}_2-{\mathbf{q}}_1\right)$$
如下图的中间图所示：对于基准点云任意4个点中得到的$r_1,r_2$,在待配准点云任意两点$q_1，q_2$,由上式可以得到2个$e_1$(由 r1计算得到)，2个$e_2$点(由 r2计算得到)。如下图中的右边图所示：对于两条线段（4个点）而言，若第一个线段中的任意一个$e_1$（一个线段两个$e_1$）与第二条线段中任意一个$e_2$（一个线段两个$e_2$）重合或者在很小距离范围内，那么可以认为这两个线段对应的四个端点，可能是基准点云中4个点的对应点。
如下图：

2.2在3维空间中寻找4个共面点集对

给定从点集P和另一点集Q中选择的（近似）共面点的4点基B∈ R3，我们的目标是从Q中提取与B近似相等的所有4个点的集合。首先给出B，我们计算它在这个平面上的两个仿射不变量比，如前所述。
然后，使用第3.2节中描述的方法，从点Q中，通过仿射变换提取与B相关的所有点集。虽然此方法能够获得所需4点的共面点集，但是会存在一定数量的虚假匹配。
为了去除非全等基，我们查看它们在点云中的原始位置，并验证相应的集是否在某个距离阈值内与基集B一致。然后，使用基B和Q中的每个基，通过最小二乘计算最佳对齐刚性变换。

上述程序需要大量内存，对于大量点云是不合适的。做出以下改进：刚性变换保持点间欧氏距离。给定基数B≡ {a，b，c，d}，我们首先计算距离d1=‖a− b‖和d2=‖c− d‖。现在我们只考虑Q中的的距离为d1或d2的点对，最大误差为δ。

3 4PCS算法

我们给出了两个点集P和Q，这些点的位置精度的不确定性度量（δ>0），以及P中可与Q重叠区域分数f的估计方法。我们的目标是找到一种刚性变换，使P中的最大点数与Q中某个点之间的距离小于δ。我们提出了一种算法（见算法1），其运行时间取决于给定点集之间匹配点数的最大值，并将其随机化，以很高的概率发现正确的刚体变换。

我们首先选择一个由由4个共面点组成的基B⊆ P。实际上，我们允许一些非平面性，因为不太可能存在4个共面点。我们随机选取三个点，并选择剩余点，使四个点一起形成一个widebase，该base（近似）共面。通过选择彼此相距较远的点来创建widebase，从而产生更稳定的共面点。然而，如果我们选择的点相距太远，所选的点可能不会全部位于重叠区域（用于部分匹配）。我们使用重叠分数f来估计这个最大距离。如果没有提供f的估计值，我们将在f=1，0.5，0.25，…的情况下以减少猜测的方式运行该算法。直到我们达到所需的误差容限。在f已知的情况下，我们首先选择一组可能位于重叠区域的三个点，然后如前所述选择第四个点。

对于从算法的SELECTCOPLANARBASE阶段获得的平面基B，我们可以使用基点定义仿射不变比率。然而，对于近似平面基底，我们使用位于连接点对的的最近点来定义不变比率。现在，我们应用第2.1和2.2节中描述的方法来提取集合U≡ Q中的4个点的所有子集的{U1，U2，…，Us}，它们可能与B一致。对于每个Ui，使用B和Ui之间的对应信息，我们计算使B在最小二乘意义上接近Ui的最佳对齐刚性变换Ti【Horn 1987年】。为了验证Ti，我们计算Ti*（P），并计算Ti*（P）中有多少点比δ更接近Q中的某个点。为Ti评分（参见[Irani和Raghavan 1996]）。选取评分最高的Ti，为最终的变换T。

给定一个基Bi，我们描述了如何计算与其对应的最佳变换Ti。根据对齐的点数，为每个对齐变换Ti分配一个分数。使用该程序，我们现在执行Randomized Alignment过程，并根据重叠分数f的估计值，测试出L个不同的基（见公式1）。在所有这些试验中，我们选择得分最高的变换矩阵Topt。

4 一些加速技术

配合局部特征描述子和局部特征（曲率，法线），加速4点共面点集的选择过程。

5 4pcs在pcl中应用

#pragma once
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <iostream>
#include <pcl/registration/ia_fpcs.h>
#include <pcl/registration/ia_kfpcs.h>
#include <time.h>
#include <boost/thread/thread.hpp>


using namespace std;
typedef pcl::PointXYZ PointT;
typedef pcl::PointCloud<PointT> PointCloud;



int fourpcs(const pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_source,
	const pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_target,
	pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_source)
{




	//四点法配准
	PointCloud::Ptr pcs(new PointCloud);
	pcl::registration::FPCSInitialAlignment<pcl::PointXYZ, pcl::PointXYZ> fpcs;

	fpcs.setInputSource(cloud_source);//输入待配准点云
	fpcs.setInputTarget(cloud_target);//输入目标点云

	//参数设置
	fpcs.setApproxOverlap(0.6);//两点云重叠度
	fpcs.setDelta(0.5);//Bunny
	//fpcs.setDelta(0.5);//hippo
	fpcs.setMaxComputationTime(50);
	fpcs.setNumberOfSamples(int(cloud_source->size()/20));
	Eigen::Matrix4f tras;
	clock_t start = clock();
	fpcs.align(*pcs);
	clock_t end = clock();
	cout << "time:" << (double)(end - start) / (double)CLOCKS_PER_SEC << endl;
	cout << "score:" << fpcs.getFitnessScore() << endl;
	tras = fpcs.getFinalTransformation();
	cout << "matrix:" << endl << tras << endl << endl << endl;


	//PointCloud::Ptr cloud_end(new PointCloud);
	pcl::transformPointCloud(*cloud_source, *transformed_source, tras);
	//visualize_pcd(cloud_source, cloud_target, cloud_end);
	return (0);
}

参考：
《4-Points Congruent Sets for Robust Pairwise Surface Registration》
https://blog.csdn.net/qq_41102371/article/details/111293664
https://blog.csdn.net/Ha_ku/article/details/79480613
https://blog.csdn.net/renyuanxingxing/article/details/84662986
https://blog.csdn.net/qq_41102371/article/details/111715115