【智能算法】原子搜索算法（ASO）原理及实现

小O的算法实验室

于 2024-04-06 11:16:27 发布

阅读量3.8k

点赞数 16

分类专栏：智能算法文章标签：智能算法算法

本文链接：https://blog.csdn.net/Logic_9527/article/details/137422930

版权

智能算法专栏收录该内容

474 篇文章

订阅专栏

本文介绍了一种受原子运动规律启发的优化算法——原子搜索算法(ASO)，它利用分子动力学原理和种群中原子间相互作用力进行智能搜索。算法详细阐述了加速度计算、相互作用力和约束力模型，以及基于适应度值的个体质量调整。结果展示了ASO在地下水分散系数估计中的应用潜力。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述

1.背景

2019年，Zhao等人受到原子运动规律启发，提出了原子搜索算法（Atom Search Algorithm，ASO）。

2.算法原理

2.1算法思想

ASO根据分子动力学中原子的物理运动规律建立，通过种群中各个原子之间的相互作用力来指导群体进行智能优化搜索。

2.2算法过程

根据牛顿第二定律，如果Fi是作用在第i个原子上的相互作用力，而Gi是作用
在第i个原子上的约束力，该原子的质量为mi，那么第i个原子的加速度为：
$a_i=\frac{F_i+G_i}{m_i}\tag{1}$

相互作用力Fi:

相互作用力 Fi表示周围原子对当前原子 i 的作用力之和:
$F_{i}^{d}\left(t\right)=\sum_{j\in K_{\mathrm{best}}}rand_{j}F_{ij}^{d}\left(t\right)\tag{2}$

其中，d为原子所在的维数。Kbest为对原子i产生作用力的原子的集合；Fijd(t)为第t次迭代中第j个原子对原子i的伦纳德·琼斯(L-J)势作用力：
$K_{\mathrm{best}}(t)=N-(N-2)\cdot\sqrt{\frac{t}{T}}\tag{3}$

Fijd(t)定义为：
$F_{ij}^d(t)=-\eta\left(t\right)\left[2\bigl(h_{ij}(t)\bigr)^{13}-\bigl(h_{ij}(t)\bigr)^{7}\right]\tag{4}$
在这里插入图片描述

η(t)为用于调整排斥区域或吸引区域的深度函数:
$\eta\left(t\right)=-\alpha\left(1-\frac{t-1}{T}\right)^3\mathrm{e}^{-\frac{20t}{T}}\tag{5}$

hij标准定义为：
$h_{ij}=\frac{r_{ij}(t)}{\sigma(t)}\tag{6}$
σ为长度尺度，表示碰撞直径；rij为2个原子之间的欧几里得距离:
$\begin{aligned}&r_{ij}(t)=\left\|x_{i}(t),x_{j}(t)\right\|_{2}\\&\sigma(t)=\left\|x_{i}(t),\frac{\sum_{j\in K_{\mathrm{best}}(t)}x_{j}(t)}{K_{\mathrm{best}}(t)}\right\|_{2}\end{aligned}\tag{7}$
为了改善勘探范围，论文中将表现为斥力的 h 的下限设置为 hmin=1.1，上限设置为 hmax=2.4，并且在hmin的基础上增加了一个正弦扰动函数g(t):
$h_{ij}\left(t\right)=\begin{cases}h_{\min}+g(t)&\frac{r_{ij(t)}}{\sigma(t)}<h_{\min}\\\\\frac{r_{ij(t)}}{\sigma(t)}&h_{\min}\leqslant\frac{r_{ij(t)}}{\sigma(t)}\leqslant h_{\max}\\\\h_{\max}&\frac{r_{ij(t)}}{\sigma(t)}>h_{\max}\end{cases}\tag{8}$
g(t)定义为：
$g(t)=0.1\sin\left(\frac{\pi}{2} \cdot \frac{t}{T}\right)\tag{9}$
在这里插入图片描述

共价键约束力Gi:

为了突出种群最佳原子的引导作用，假设每个原子与种群最佳原子具有一个共价键，因此每个原子都要受到最佳原子的约束力作用:

$G_i^d=\beta\mathrm{e}^{\frac{-20t}{T}}\Big( x_{\mathrm{best}}^d( t ) -x_i^d( t ) \Big)\tag{10}$

原子加速度ai:

结合相互作用力和几何约束力，在时间t的第i个原子在第d维上的加速度:
$\begin{aligned} a_i^d= \frac{F_i^d+G_i^d}{m_i(t)}= -\alpha\left(1-\frac{t-1}T\right)^3\mathrm{e}^{-\frac{20t}T}\sum_{j\in K_{\mathrm{best}}}\frac{rand_j\left[2\left(h_{ij}\left(t\right)\right)^{13}-\left(h_{ij}\left(t\right)\right)^7\right]}{m_i\left(t\right)}+ \beta\mathrm{e}^{-\frac{20t}T}\frac{\left(x_{\mathrm{best}}^d(t)–x_i^d(t)\right)}{m_i} \end{aligned}\tag{11}$
第t次迭代中第i个原子的质量mi(t)由当前种群个体的适应度值大小决定:
$M_{i}(t)=\mathrm{e}^{-\frac{f_{i}(t)-f_{\min}(t)}{f_{\max}(t)-f_{\min}(t)}}\\m_{i}(t)=\frac{M_{i}(t)}{\sum_{j=1}^{N}M_{i}(t)}\tag{12}$
其中，fmax(t)和fmin(t)分别表示原子种群中最大适应度值和最小适应度值。

位置更新：

更新公式：
$\begin{aligned}&\nu_{i}^{d}\left(t+1\right)=rand_{i}^{d}\nu_{i}^{d}\left(t\right)+a_{i}^{d}\left(t\right)\\&x_{i}^{d}\left(t+1\right)=x_{i}^{d}\left(t\right)+\nu_{i}^{d}\left(t+1\right)\end{aligned}\tag{13}$
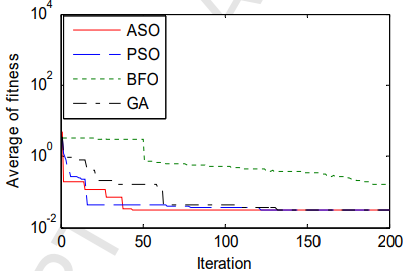
在这里插入图片描述

伪代码：
在这里插入图片描述

3.结果展示

在这里插入图片描述

4.参考文献

[1] Zhao W, Wang L, Zhang Z. A novel atom search optimization for dispersion coefficient estimation in groundwater[J]. Future Generation Computer Systems, 2019, 91: 601-610.