【论文复现】通过多策略增强的麻雀搜索优化算法用于高维优化问题

---

1.摘要

随着科技的进步，高维全局优化问题在基因识别、车辆路线规划、工作调度和网络拓扑等科研和工程领域变得越来越常见。这些问题的特点是搜索空间庞大且复杂，局部最小值众多，这使得在有限的计算资源下找到全局最优解极具挑战性。为应对这些挑战，本文提出了一种基于仿生方法的增强型麻雀搜索优化算法（ESSSO）。ESSSO结合了多种策略：一种基于von Mises分布的自适应正弦行走策略、一种利用轮盘赌选择的学习策略、一个两阶段演化策略以及选择突变策略。这些策略不仅提高了搜索的多样性和全局搜索能力，而且优化了种群的进化效率，平衡了探索和开发，有效提升了算法的性能。

2.麻雀搜索算法SSA原理

【智能算法】麻雀搜索算法（SSA）原理及实现

3.改进策略

基于von Mises分布的自适应正弦行走策略(ASW)

在优化问题的解决方案中，控制搜索步长可以保证搜索在解空间的充分性和有效性。本文提出了一种自适应正弦行走策略（ASW），基于von Mises分布分布（VMD），通过将搜索步长与搜索范围相结合，实现了步长的自适应调整，提高了算法的适应性。von Mises分布是一种圆上的连续概率分布，有助于模拟正态分布并增强种群多样性：
$$X_i^{t+1}=\{\begin{array}{ll}{X}_i^t\cdot exp(\frac{-i}{R_1\cdot ite{r}_{max}})& R_2<ST\\ X_i^t+sin({\Theta }_i^t)\cdot \frac{(U_{pper-Lower})}{\alpha }& Otherwise\end{array}$$
其中，参数表述为：
$${\Theta }_i^t=circ\_vmrnd(\theta ,\phi )$$

基于轮盘赌选择的学习策略

在标准SSA算法框架下，处于有利位置的追随者通过学习当前最优解来改变自身位置。然而，迭代初期的当前最优解可能与全局最优解有较大偏差，这可能导致算法过早地收敛到非最优解。为了防止这种情况，引入了轮盘赌选择（RWS）策略，这种策略通过计算个体的适应度和选择概率来随机选择个体，从而保持种群的多样性和高质量的父代。此外，为增强算法的全局搜索能力，我们提出了一种基于轮盘赌选择的学习策略（LSR），通过引入随机位置来进一步保持种群多样性：
$$X_i^{t+1}=X_i^t+rand\cdot \left|X_{random}^t-X_i^t\right|+rand\cdot \left|X_R^t-X_i^t\right|$$
参数$R$计算公式为：
$$\begin{gathered} R^t=RWS(1,\mathbb{F}(X^t)) \\ \mathbb{F}(X^t)=exp(\frac{f(X^t)}{\frac{1}{N}{\sum }_{i=1}^N\left|f(X_i^t)+\epsilon \right|}) \end{gathered}$$

两阶段进化策略

在麻雀搜索算法（SSA）中，随着迭代过程的进行，麻雀种群中的追随者会逐渐靠近解空间中的最优位置，这有助于提高算法的收敛速度。然而SSA算法进入后期迭代阶段时，所有个体往往会聚集在最优位置周围，最终固定在当前最优解的位置，这使得算法易于陷入局部最优。为了解决这一问题并提升算法在迭代后期的全局搜索能力，本文提出了一种两阶段演化策略（TSE），这种策略旨在帮助算法突破局部最优，从而更有效地探索整个解空间。

为加速收敛速度，我们提出了一种基于von Mises分布的正弦学习机制（SLM），该机制针对每代中适应度较低的子群体。在此机制中，每个个体通过正弦函数学习最优解：
$$X_i^{t+1}=X_i^t+sin({\Theta }_i^t)\cdot X_{best}^t$$
其中，$\theta$表述为：
$$\theta =\frac{pi}{2}\cdot \frac{f(X_{best}^t)}{f(X_i^t)}$$

在迭代过程中，种群多样性逐渐降低，这可能导致算法陷入局部最优，难以寻找全局最优解。因此，我们提出了一种适应性突变机制（AMM），旨在通过增强种群多样性：
$$\begin{array}{rl}{X}_i^{t+1}& =X_{best}^t+a{f}_i^{t+1}\cdot TDR\cdot randsrc(1,D)\\ & \cdot [(Upper-Lower)\cdot rand(1,D)+Lower]\end{array}$$
其中，TDR为行进距离速率，可自适应调整：
$$TDR=1-\frac{(iter{)}^{1/6}}{(ite{r}_{max}{)}^{1/6}}$$
$$a{f}_i^{t+1}=\{\begin{array}{ll}\frac{f(X_i^{t-1})-f(X_i^t)}{{\sum }_{i=1}^N(f(X_i^{t-1})-f(X_i^t))+ϵ}+\eta & t\ge 2\\ 0.5& t=1\end{array}$$
因此，位置更新：
$$X_i^{t+1}=\{\begin{array}{cc}{X}_{best}^t+a{f}_i^{t+1}\cdot TDR\cdot randsrc(1,D)& \\ \cdot [(Upper-Lower)\cdot rand(1,D)+Lower]& i>\frac{3N}{4}\\ X_i^t+sin({\Theta }_i^t)\cdot X_{best}^t& \frac{3N}{4}\ge i>\frac{N}{2}\\ X_i^t+rand\cdot \left|X_{random}^t-X_i^t\right|+rand\cdot \left|X_R^t-X_i^t\right|& otherwise\end{array}$$

为了提高收敛速度同时保持种群多样性，我们引入了一种选择突变策略（SMS）：
$$X_i^{t+1}=\{\begin{array}{ll}{X}_{best}^t+\beta \cdot ({\tilde{X}}_i^{t+1}-X_{best}^t)& iff(X_i^t)\ne f(X_{best}^t)\\ X_i^t+\kappa \cdot \frac{|X_i^t-X_{worse}^t|}{(f(X_i^t)-f(X_{worse}^t))+ϵ}& Otherwise\end{array}$$

流程图

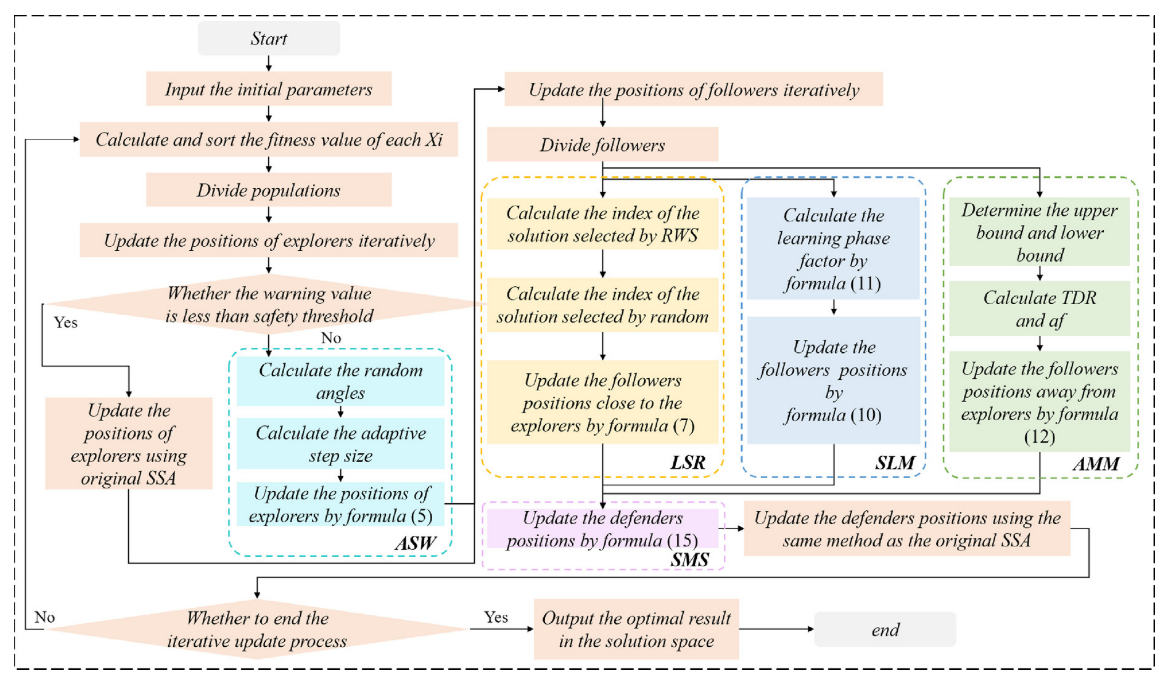
伪代码

4.结果展示

CEC2017-50dim

5.参考文献

[1] Liang S, Yin M, Sun G, et al. An enhanced sparrow search swarm optimizer via multi-strategies for high-dimensional optimization problems[J]. Swarm and Evolutionary Computation, 2024, 88: 101603.

6.代码获取