目录
坐标系统
UE使用笛卡尔坐标系统去表示三维欧几里得空间位置,在UE内坐标系统是左手定律且Z轴向上;点是由三个坐标轴的位置确定(x、y、z),这些坐标值设置了actor的位置和方向;这些轴可以通过多种不同的方式相互定向,轴的方向和值取决于所在的坐标空间的类型;
注,如从其他软件(Maya, Houdini, ZBrush, Blender, or 3ds Max)导入资产,需考虑坐标轴方向;


Axes
在UE中,X轴—红色、Y轴—绿色、Z轴—蓝色(向上);
- X轴,决定actor向前(forward)或向后(backward),正值向前;
- Y轴,决定actor向左(left)或向右(right),正值向右;
- Z轴,决定actor向上(up)或向下(down),正值向上;
在坐标系中有一个特别的点,称为原点(origin),由(0,0,0)表示;
可使用正交视图查看轴的方向并设置轴的值;

Transform and Control Axes

场景中心的变换小控件与视口左下角的小控件图标的方向相同,匹配方向是因为正在世界空间中查看所选演员;此外,编辑器中的变换控件的轴颜色协调匹配的;

坐标空间
每个坐标空间都有自己的坐标系和原点,轴的交点等于该特定坐标空间的原点,由该坐标空间坐标系内的坐标(0,0,0)表示,轴的值根据变换的原点和方向而增加或减少;
World Space
世界空间是相对整个关卡的坐标系统,原点是场景的中心;此坐标系统是固定的,以绝对单位位移或旋转对象;

Local Space
局部空间是相对场景组件(被赋予到actor)的坐标系统,也称之为对象空间(object space);
每个actor在场景中都有一个相对于actor枢轴点的局部空间坐标系,actor的枢轴点是actor的三个局部坐标轴相交的点,代表局部空间的原点;使用局部空间是相对于其父对象的平移或旋转;
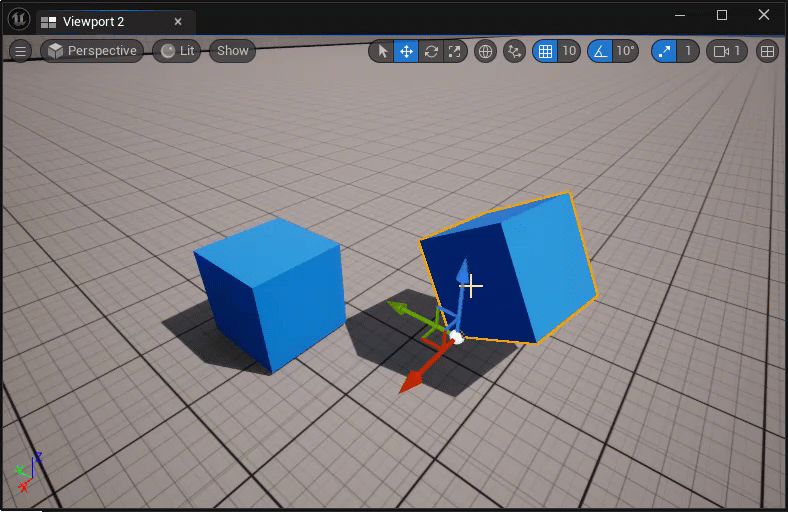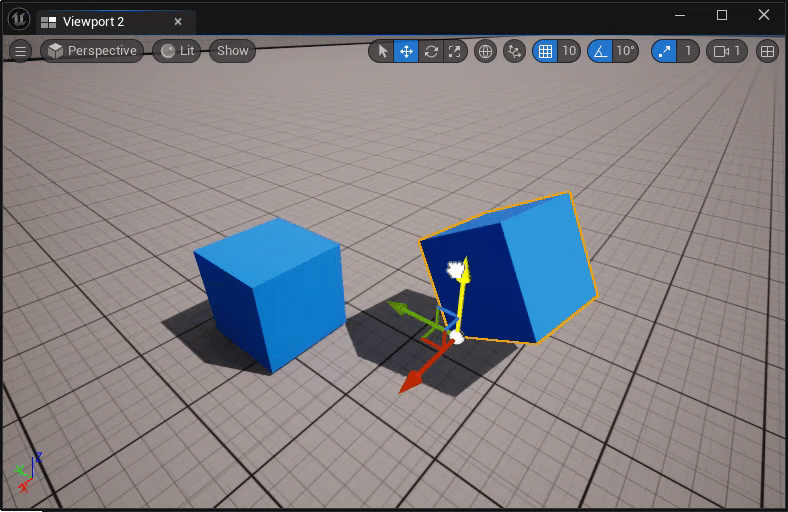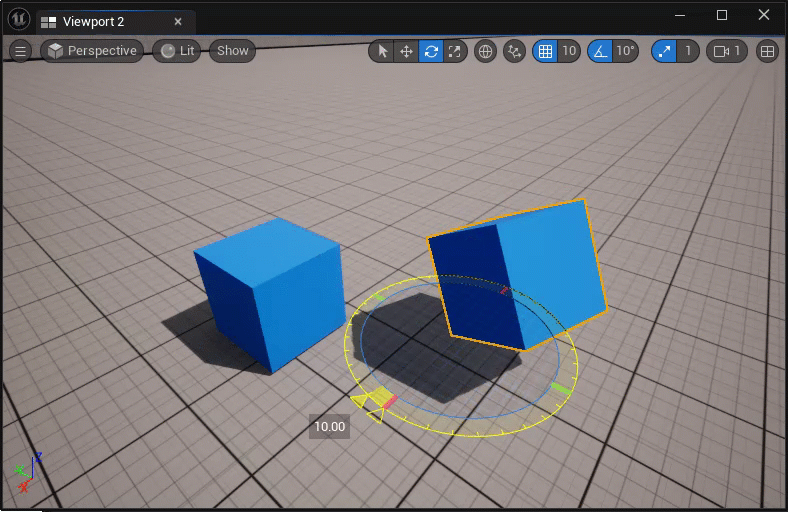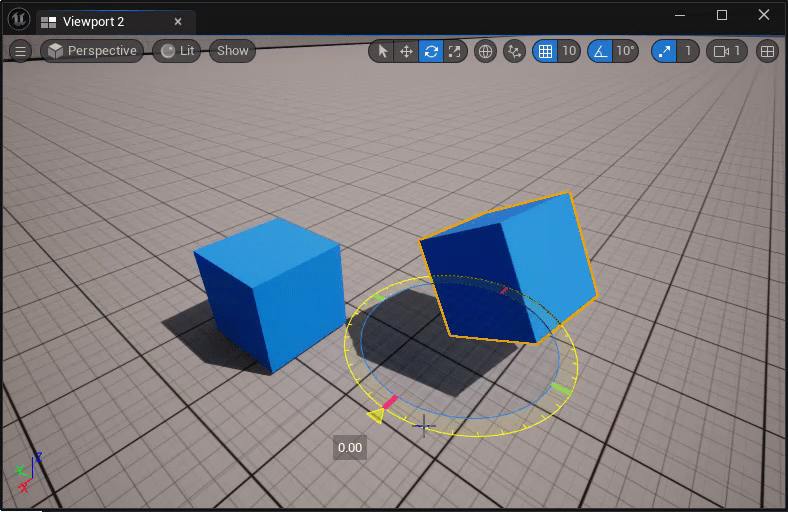
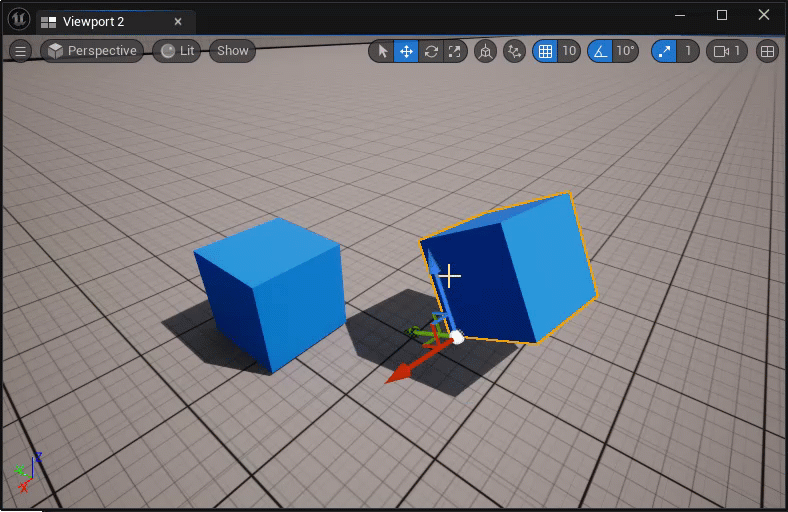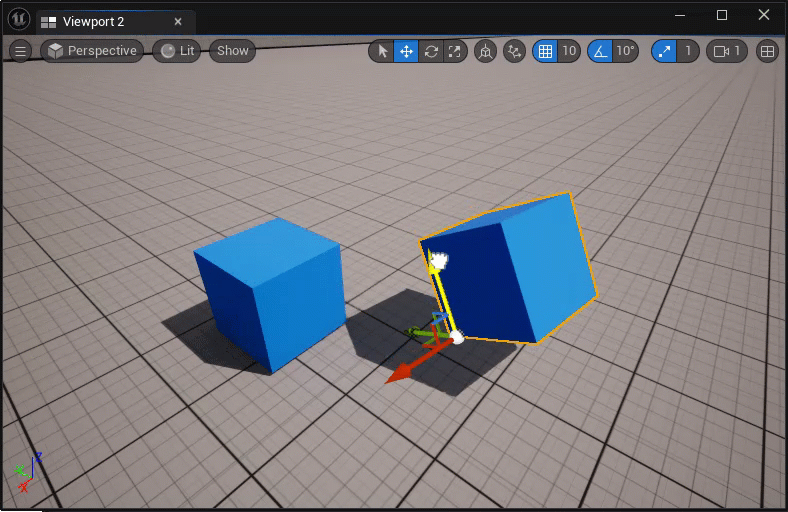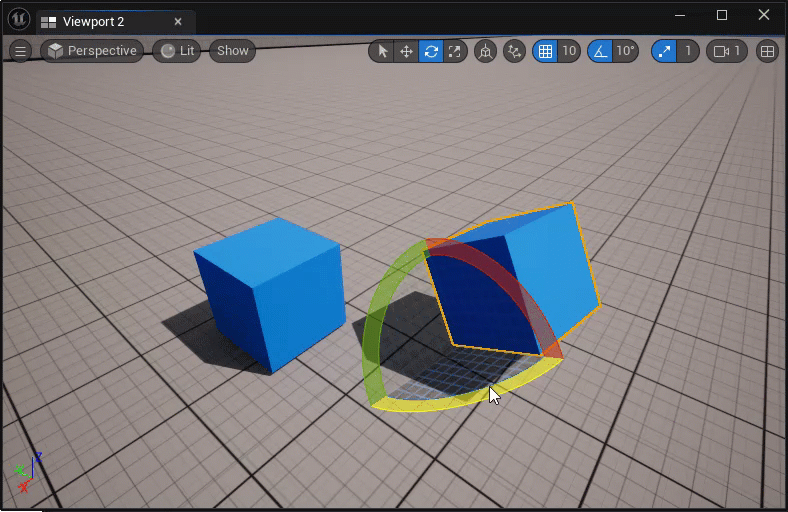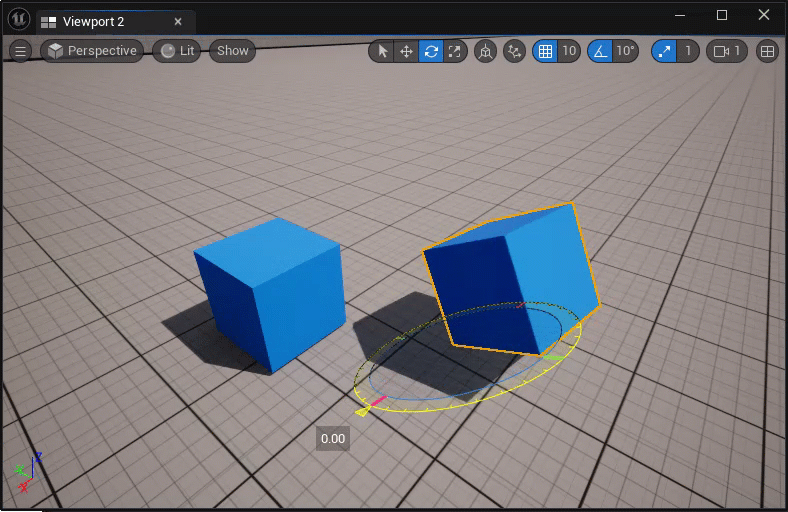
临时改变actor的枢轴点:
- 中键坐标轴控件,并拖拽移动;
- ALT + MMB,然后在新的位置处中键;
永久改变actor的枢轴点:
- 在执行临时改变枢轴点后,右击actor,选择Pivot > Set as Pivot Offset;
Screen Space
屏幕空间是将三维世界空间投影到构成玩家视觉的二维屏幕上,可从场景中的特定摄影机中提取屏幕空间坐标;

UV Space
UVs是将三维曲面网格参数化(U,V)到归一化(0-1)二维空间中;换句话说,它们表示二维空间中的坐标,这些坐标转换为三维模型上的顶点;空间水平表示为U,垂直表示为V,因此称为UV坐标,也称为2D或纹理坐标;



























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








