转置卷积Transposed Covn，卷积神经网络的可视化分析---ZFNet,全连接卷积神经网络---FCN

已于 2022-03-02 21:11:06 修改
阅读量720 收藏
点赞数 1
分类专栏： 深度学习 文章标签： 神经网络 深度学习 pytorch
于 2021-10-05 12:23:39 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ResumeProject/article/details/120505773
版权

转 置 卷 积 不 是 卷 积 的 逆 运 算 转置卷积不是卷积的逆运算 转置卷积不是卷积的逆运算
在这里插入图片描述

1.转置卷积（反卷积）：能增大输入的高和宽

nn.Conv2DTranspose

在这里插入图片描述

在这里插入图片描述
为什么称之为“转置”?(从形状上是逆变换)
●对于卷积Y=X★W,可以对W构造一个V,使得卷积等价于矩阵乘法Y’= VX’(撇代表flatten 拉平操作,这里Y’,X’是Y,X对应的向量版本)。

转置卷积则等价于Y’= vTX’
●如果卷积将输入从(h,w)变成了(h’,w)，同样超参数的转置卷积则从(h’, w’)变成(h, w)

注：填充和步幅的情况省略

ZFNet中的反卷积

如下图：卷积操作是低效操作，主流神经网络框架都是通过im2col+矩阵乘法实现卷积，以空间换效率。

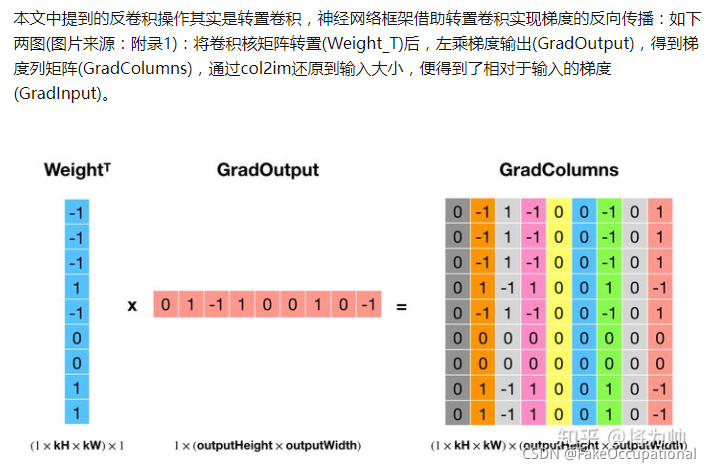
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.ZFNet

使用了解卷积和反池化（无法实现，只能近似）的近似对每一层进行可视化

在这里插入图片描述

在这里插入图片描述

彩 色 图 是 从 原 始 数 据 集 中 找 出 的 ， 能 够 使 得 特 定 层 的 某 些 卷 积 核 激 活 最 大 的 9 张 图 灰 色 图 是 由 彩 色 图 重 建 得 到 的 可 视 化 结 果 底 层 网 络 ： 边 缘 ， 颜 色 ， 中 层 网 络 ： 形 状 ， 高 层 网 咯 ： 物 体 彩色图是从原始数据集中找出的，能够使得特定层的某些卷积核激活最大的9张图\\ 灰色图是由彩色图重建得到的可视化结果 \\底层网络：边缘，颜色， 中层网络：形状， 高层网咯：物体 彩色图是从原始数据集中找出的，能够使得特定层的某些卷积核激活最大的9张图灰色图是由彩色图重建得到的可视化结果底层网络：边缘，颜色，中层网络：形状，高层网咯：物体

在训练的过程中，随着卷积核的变化（ 不同层重构的变化）
在这里插入图片描述

对于图像的平移、尺度、旋转的变化来说，网络的输出对于平移和尺度变化都是稳定的，但却不具有旋转不变性，除非目标图像时旋转对称的。

卷积核可视化：

遮挡与识别结果：

在这里插入图片描述

狗这一类别不同部位的相似性是否隐式定义(不同部位对网络结果的影响)

在这里插入图片描述

去掉某些层数：

在这里插入图片描述
迁移学习效果更好：
在这里插入图片描述

FCN

首 个 端 到 端 全 卷 积 像 素 级 分 类 网 络 首个端到端全卷积像素级分类网络 首个端到端全卷积像素级分类网络

在这里插入图片描述
最 后 重 构 的 图 片 有 k 个 通 道 ， k 为 类 别 的 个 数 ， 即 每 个 像 素 都 有 一 个 类 别 最后重构的图片有k个通道，k为类别的个数，即每个像素都有一个类别 最后重构的图片有k个通道，k为类别的个数，即每个像素都有一个类别

covn函数
qq_18343569的博客
11-19 3777
covn函数： 主要进行N维上的卷积，就是【 m n k】三维矩阵上的卷积 N-dimensional convolution Syntax C = convn(A,B) C = convn(A,B,'shape') Description C = convn(A,B) computes the N-dimensional convolution of t
计算机视觉的应用29-卷积神经网络(CNN)中的变种：分组卷积、转置卷积、空洞卷积的计算过程
微学AI的博客
04-27 1758
大家好，我是微学AI，今天给大家介绍一下计算机视觉的应用29-卷积神经网络(CNN)中的变种：分组卷积、转置卷积、空洞卷积的计算过程。分组卷积将输入通道分为几组，对每组独立进行卷积操作，以减少计算量和模型参数。转置卷积也称为反卷积，它通过将输入特征图的元素扩展到更高维度的输出特征图来执行上采样。空洞卷积通过在输入特征图上引入“空洞”或“间隙”来增加感受野，从而在不增加额外参数的情况下扩大卷积核的有效覆盖范围。
直接理解转置卷积（Transposed convolution）的各种情况
https://www.cnblogs.com/qizhou/
10-29 722
　　使用GAN生成图像必不可少的层就是上采样，其中最常用的就是转置卷积(Transposed Convolution)。如果把卷积操作转换为矩阵乘法的形式，转置卷积实际上就是将其中的矩阵进行转置，从而产生逆向的效果。所谓效果仅仅在于特征图的形状，也就是说，如果卷积将特征图从形状a映射到形状b，其对应的转置卷积就是从形状b映射回形状a，而其中的值并不一一对应，是不可逆的。另外，不要把逆卷积...
转置卷积与卷积的实现(Pytorch)与可视化(Tensorboard)
对方正在输入中...
01-24 2095
代码(code)： import torch.nn as nn import cv2 from torch.utils.data import DataLoader from torchvision import transforms from torch.utils.tensorboard import SummaryWriter img = cv2.imread("1.jpg") tran_tensor = transforms.ToTensor() img = tran_tensor(img) pr
转置卷积(Transposed Convolution)可视化过程
weixin_53598445的博客
05-11 950
转置卷积（Transposed Convolution）经常也被称作反卷积，所谓反卷积即为通过标准卷积层生成的输出被反卷积，将得到原始输入。而转置卷积不按值反转标准卷积，而仅按维度。转置卷积层和标准卷积层的计算原理完全相同，不同的是输入特征图不同。下面分别介绍标准卷积和转置卷积。，这篇博客只介绍转置卷积的具体实现。转置卷积的用处主要是对特征图进行上采样；转置卷积其实也是一种标准卷积，只不过要先根据输入的参数对输入特征图进行修改，也就是填充操作；转置卷积在滑动点积操作时的Padding和。
【机器学习】详解 转置卷积 (Transpose Convolution)
闻韶
11-08 3万+
【机器学习】详解 转置卷积 (Transpose Convolution)
基于反卷积的卷积神经网络特征可视化.zip
05-27
在这个"基于反卷积的卷积神经网络特征可视化"项目中，我们聚焦于VGG-19，这是一个由牛津大学视觉几何组（Visual Geometry Group）开发的深度卷积网络模型。VGG-19以其深而窄的架构著名，包含19个卷积层和全连接层，...
基于PyTorch的U-Net深度学习模型用于医学影像分割及SKConv增强
最新发布
02-03
主要组成部分有：卷积操作、下采样（Max Pooling）、上采样（Upsampling 或 Transposed Convolution）、以及最终的1x1卷积输出层，还有创新加入的SKConv注意力机制模块来提高网络性能。U-Net是一种对称的收缩和扩展...
Python-TensorFlow全卷积网络的可视化解决方案
与传统卷积神经网络（CNN）在图像分类任务中通常以全连接层作为输出不同，FCN的输出层也是卷积层，这使得它能够输出与输入图像同样大小的分割图。FCN可以捕捉局部特征，并能处理任意大小的输入图像，非常适合图像...
Visualize-Mnist:使用转置卷积可视化Mnist卷积特征图
05-11
在深度学习领域，尤其是卷积神经网络（Convolutional Neural Networks, CNN）中，理解模型是如何处理输入数据的是一项重要任务。"Visualize-Mnist"项目正是为了帮助我们直观地理解CNN在处理MNIST手写数字数据集时的...
转置卷积(反卷积)
qxqsunshine的博客
12-28 491
借鉴于此个博客，写的非常好：https://blog.csdn.net/isMarvellous/article/details/80087705 转置卷积（Transposed Convolution）也叫做反卷积（Deconvolution） Pytorch中可以使用torch.nn.ConvTranspose2d（）来调用，caffe中对应的转置卷积层为deconv_layer 作用：...
Caffe FCN：可视化featureMaps和Weights(C++)、获取FCN结果
alppkk4545的博客
03-09 208
为何不使用C++版本FCN获取最后的分割掩模，何必要使用python呢！因此需要获取网络最后层的featureMaps，featureMaps的结果直接对应了segmentation的最终结果，可以直接用于掩模分析。 caffe源码给出了提取中间层featureMap的源代码，位置在tools/extract_features...
转置卷积（Transposed Convolution）
热门推荐
霹雳吧啦Wz
10-13 4万+
import torch import torch.nn as nn def transposed_conv_official(): feature_map = torch.as_tensor([[1, 0], [2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2]) print(feature_map) trans_conv = nn.ConvTranspose2
反卷积(Transposed conv deconv)实现原理（通俗易懂）
weixin_39326879的博客
10-16 4万+
什么是卷积 卷积就是把卷积核放在输入上进行滑窗，将当前卷积核覆盖范围内的输入与卷积核相乘，值进行累加，得到当前位置的输出，其本质在于融合多个像素值的信息输出一个像素值，本质上是下采样的，所以输出的大小必然小于输入的大小，如下图所示： 什么是反卷积 反卷积和转置卷积都是一个意思，所谓的反卷积，就是卷积的逆操作，我们将上图的卷积看成是输入通过卷积核的透视，那么反卷积就可以看成输出通过卷积核的透视，具体如下图所示： 比如左上角的图，将输出的55按照绿色的线的逆方向投影回去，可以得到[[55,110,55],
tensorflow 中反卷积操作（transpose conv）详解
卓为的博客
03-15 4036
题主花了很多时间去理解 tensorflow 中 transpose_conv 的计算方法，终于找到了一篇写得比较基础的博文link，文中用 python 实现了 tensorflow 中 transpose_conv 的功能，但是存在一点点不足，code仅仅适合 stride=2,kernel=3的场合，现修改其代码，使其适应于 stride = 2,但kernel 可以为任意值的场合。 ...
3.TransposedConv2d实现 （含dilation）
weixin_42216799的博客
11-18 1362
反卷积介绍及C++实现
转置卷积(transposed-convolution)
m0_56312629的博客
03-21 6273
本文介绍了转置卷积，介绍了转置卷积的背景、对反卷积的误解以及转置卷积的计算，最后用代码实现了转置卷积，并比较了常规卷积与转置卷积在padding、stride和通道参数的不同1.
一文详解转置卷积(Transpose Convolution)
墨城的博客
10-29 1259
​ 通常情况下，对图像进行卷积运算时，经过多层的卷积运算后，输出图像的尺寸会变得很小，即图像被削减。而对于某些特定的任务（比如：图像分割、GAN），我们需要将图像恢复到原来的尺寸再进行进一步的计算。这个恢复图像尺寸，实现图像由小分辨率到大分辨率映射的操作，叫做上采样（Upsample），如 图 所示。
详解FCN模型中每一层的输出及可视化操作
花生米
12-21 5347
对于FCN模型的搭建以及训练自己的数据集，其实并不是特别难。可以参考FCN训练自己的数据集。可能更多的人想知道FCN每一层输出的结果是什么。这篇博客主要介绍的是对FCN每一层输出进行可视化操作。 查看FCN总体框架 先打开工具netcope，然后打开fcn-master2\voc-fcn32s下的train.prototxt文件，将train.prototxt文件内容复制到网页左侧编辑框后，sh...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值