【雷达】调频连续波雷达多运动目标检测（Matlab代码实现）

最新推荐文章于 2025-05-22 10:59:32 发布

长安程序猿

最新推荐文章于 2025-05-22 10:59:32 发布

阅读量689

点赞数 8

文章标签：目标检测 matlab 目标跟踪

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147645391

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

调频连续波雷达（FMCW）多运动目标检测研究

一、FMCW雷达基本原理

二、多运动目标检测的关键挑战

三、多目标检测主流方法

四、信号处理技术实现

五、研究现状与挑战

六、典型实验案例

七、未来研究方向

总结

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

调频连续波雷达（FMCW）多运动目标检测研究

一、FMCW雷达基本原理

FMCW雷达通过发射频率随时间线性调制的连续波（如三角波、锯齿波或正弦波），接收目标反射的回波信号后，利用发射与回波信号的频率差（差频信号）计算目标距离和速度。其核心原理包括：

频率调制与差频生成：发射信号频率按调制波形（如三角波）周期性变化，回波信号因传播延迟产生时延，导致与发射信号的瞬时频率差（Δf），该差频与目标距离成正比（Δf = 2Sd/c，S为调频斜率，d为距离）。
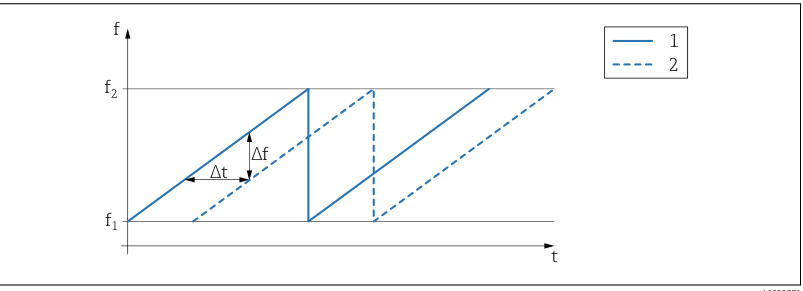
混频与信号处理：通过混频器将回波与发射信号混合，生成中频（IF）信号，经滤波和模数转换后，利用快速傅里叶变换（FFT）提取频率信息。
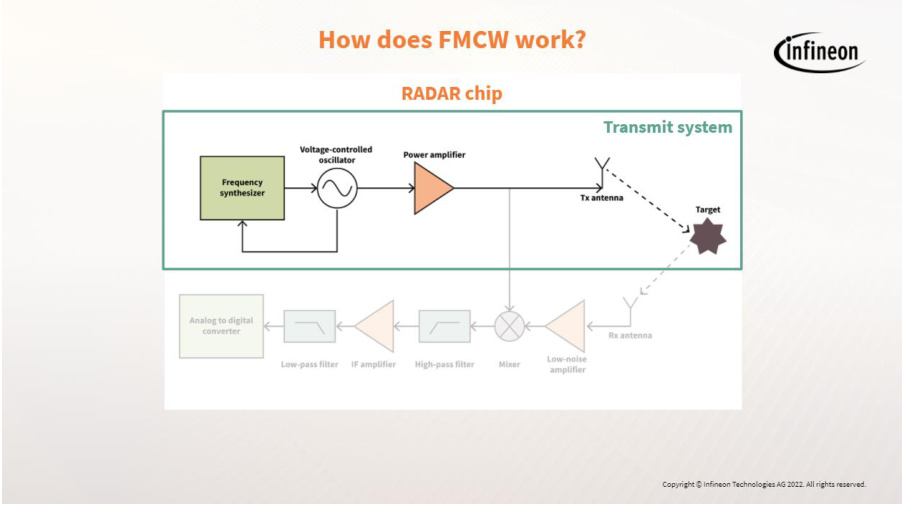
测速原理：利用多普勒效应引起的相位变化，通过多个调频周期（Chirp）间的相位差计算目标速度（v = λΔφ/(4πTc)，Tc为Chirp周期）。

二、多运动目标检测的关键挑战

信号分离难题：
- 距离-速度耦合：单Chirp内运动目标的距离和速度信息耦合，需通过双调频斜率（如三角波的正负斜率）解耦。
- 频谱混叠：目标间距小于距离分辨率时，FFT无法区分，需增大带宽或采用超分辨率算法（如MUSIC、压缩感知）。
动态环境干扰：
- 多普勒模糊：高速目标导致多普勒频移超出Nyquist范围，需通过改进CRT（中国余数定理）或波形设计解模糊。
- 多径效应：复杂环境中的反射信号需通过多径抑制算法处理。
实时性与计算复杂度：自动驾驶等场景要求毫秒级响应，传统FFT（复杂度O(NlogN)）需优化，或结合GPU加速和深度学习模型。

三、多目标检测主流方法

基于FFT的二维处理：
- 距离-多普勒图（RDM） ：快时间维（单个Chirp采样）FFT提取距离信息，慢时间维（跨Chirp）FFT提取速度信息，生成二维谱图，结合恒虚警率（CFAR）检测峰值。
- 性能指标：距离分辨率ΔR = c/(2B)，速度分辨率Δv = λ/(2NTc)，B为带宽，N为Chirp数量。
压缩感知技术：
- 利用稀疏信号特性，通过正交匹配追踪（OMP）等算法从少量测量中恢复目标参数，分辨率较FFT提升2-3倍，适用于MIMO雷达稀疏阵列。
相位补偿与超分辨率算法：
- 动目标补偿：针对TDM-MIMO雷达的相位偏移，采用Kaiser窗FFT波束成形补偿多普勒频偏，提升角度估计精度。
- MUSIC/ESPRIT：基于子空间分解的超分辨率算法，提高角度分辨能力，但计算复杂度较高。
深度学习与数据融合：
- 训练卷积神经网络（CNN）识别距离-多普勒图中的目标特征，结合多传感器（激光雷达、摄像头）数据提升鲁棒性。

四、信号处理技术实现

硬件架构：
- 发射端：频率合成器、压控振荡器（VCO）、功率放大器（PA）生成调频信号。
- 接收端：低噪声放大器（LNA）、混频器、低通滤波器（LPF）提取差频信号，ADC转换为数字信号。
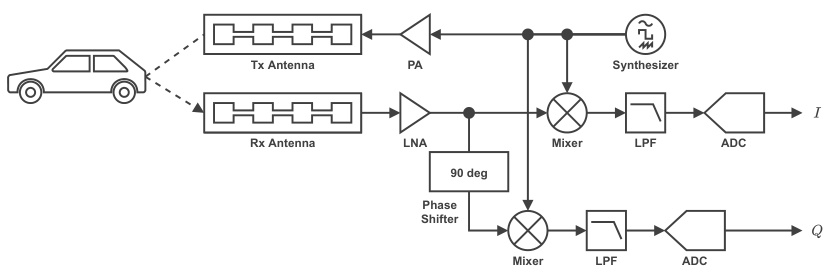
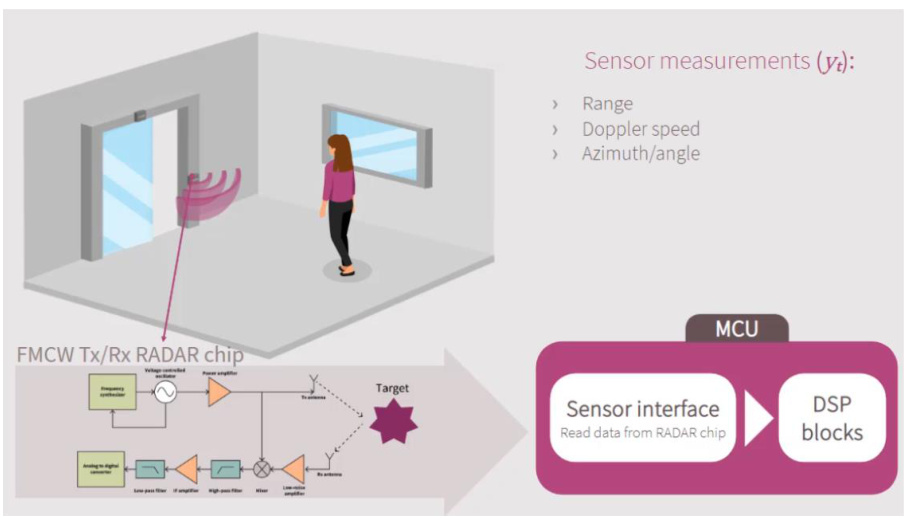
数字信号处理流程：
- 距离FFT：单Chirp内采样数据FFT，获取目标距离。
- 速度FFT：跨Chirp相位变化FFT，计算速度。
- 角度估计：多天线接收信号通过DBF（数字波束成形）或MUSIC算法提取角度。

五、研究现状与挑战

当前进展：
- 高精度算法：如局部极大值同步提取变换（LM-SET）将无人机旋翼叶长估计误差降低27.7%。
- 多目标跟踪：基于损失函数的联合概率互联（LJPDA）算法在关联精度和实时性上优于传统JPDA。
未解决问题：
- 密集目标分离：目标间距接近时，现有算法易产生虚警或漏检。
- 动态环境适应性：雨雪、电磁干扰等复杂场景需开发自适应滤波算法。
- 硬件资源限制：超分辨率算法（如压缩感知）对计算资源要求高，难以在嵌入式平台实时运行。

六、典型实验案例

汽车防撞雷达仿真：
- 改进FMCW调制波形（三角波+锯齿波组合），结合多目标识别算法，成功从16个虚假目标中筛选出4个真实目标，相对速度误差<5%。
生命体征检测：
- MIMO-FMCW雷达通过DBSCAN聚类和LCMV波束成形，实现多人呼吸/心跳频率检测，平均误差<10%。
无人机微动特征提取：
- 多波段FMCW雷达数据集（LSS-FMCWR-1.0）结合LM-SET算法，提升时频分辨率和参数估计精度。

七、未来研究方向

多模态融合：融合雷达与视觉/激光雷达数据，解决极端天气下的目标检测问题。
量子雷达技术：探索量子纠缠特性以提升抗干扰能力和分辨率。
低功耗ASIC设计：开发专用芯片优化算法硬件实现，满足物联网设备需求。

总结

FMCW雷达多运动目标检测技术已在高精度测距测速、动态环境适应性和多目标分离等方面取得显著进展，但仍需在算法效率、复杂场景鲁棒性和硬件优化上进一步突破。随着深度学习与新型信号处理技术的结合，未来有望在自动驾驶、智能安防等领域实现更广泛的应用。

📚2 运行结果

主函数部分代码：

clear all;
close all;
load fmcwmatlab2018data;
x=cube;
[nrn,nan]=size(x);
matchingcoeff=getMatchedFilter(waveform);
mlength=length(matchingcoeff);
lambda=c/fc;

fx=fftshift((linspace(-prf/2,prf/2-prf/nan,nan))*2*pi);
Vel=-fx/2*lambda/2/pi;
ts=(0/fs:1/fs:(nrn-1)/fs).';

% Eliminating the frequency shift in frequncy domain
x=fft(x,nrn,1);
x=fft(x,nan,2);
u=exp(1i*4*pi/lambda*(ts*Vel));  %
u=fft(u,nrn,1);
for k=1:nan
    x3=cconv(x(:,k),u(:,k),nrn);
    x(:,k)=x3/nrn;
end
x=ifft(x,nrn,1);
x=ifft(x,nan,2);

% Construct the signal generating matrix
z=zeros(nrn,nrn-mlength);
Rs=0:Rresolution:(nrn-1)*Rresolution;
L=(4*pi*Rs*2/lambda).^2;
L=L/max(abs(L));
L=1./L;
L(1)=L(2)*1;
L(end-mlength+1:end)=ones(mlength,1);
for k=1:nrn-mlength
    z(:,k)=circshift(sig,k-1)*L(k);
end
% the noise added to the signal
noiseadd=[wgn(nrn-mlength+1,mlength,20*log10(2.0324*1e-9),'complex');zeros(mlength-1,mlength)];
for k=1:mlength
    noiseadd(:,k)=circshift(noiseadd(:,k),k-1);
end
z=[z noiseadd];
% Solve the problem throught the Least Square method
x=pinv(z'*z)*z'*x;

% Because for close range and high speed targets, the side lobe in the velocity direction is very
% high, so the chebwin window is added to lower the side lobe. This step
% perhaps is  unnecessary for far range target such as farther than 5
% meters;
w=chebwin(nan);
for k=1:nrn
    x(k,:)=x(k,:).*w.';
end

x=fft(x,nan,2);
x=fftshift(x,2);

% Because for close range and high speed targets, the side lobe severely
% effect the detection, so for far range such as farther than 5 meters, these
% lines need not be zeroed.
x(:,1)=0*x(:,1);
x(:,2)=0*x(:,2);
x(:,end)=0*x(:,end);
x(:,end-1)=0*x(:,end-1);