为什么传递函数的闭环极点都在复平面的左半平面的系统就是稳定系统？

星宿老仙丁春秋

已于 2024-03-11 19:20:34 修改

阅读量1.6k

点赞数 11

文章标签：经验分享

于 2024-02-28 22:16:38 首次发布

本文链接：https://blog.csdn.net/hei_shan_lao_yao/article/details/136211628

版权

一. 简介

对于一个自动控制系统而言，首先要进行的不是确定系统的性能指标能否满足要求，而是确定系统是否稳定，通常，只有稳定的自动控制系统才是人们需要的有价值的系统。

判断一个系统是否是稳定系统的原则是：系统所有的闭环极点都具有负实部，即，所有的闭环极点都位于ｓ平面的左半部分的系统是稳定系统。

二. 回到时域看为什么

以二阶系统为例，抛砖引玉，一探究竟。二阶系统的闭环传递函数为：

$\Phi (s) = \frac{Y(s)}{R(s)} = \frac{\omega _{n}^{2}}{s^{2} + 2\zeta \omega _{n} s + \omega _{n}^{2}}$

该传递函数的闭环极点（系统特征方程的根）为：

$s^{2} + 2\zeta \omega _{n} s + \omega _{n}^{2} = 0$

$\Rightarrow s_{1,2} = -\zeta \omega _{n} \pm j\omega _{n} \sqrt{1-\zeta ^{2}}$

当输入为单位阶跃信号 $R(s) = \frac{1}{s}$ 时，有

$Y(s)= \frac{\omega _{n}^{2}}{s^{2} + 2\zeta \omega _{n} s + \omega _{n}^{2}}\cdot \frac{1}{s}$

因式分解并化简得：

$Y(s) = \frac{1}{s} - \frac{1}{\sqrt{1-\zeta ^{2}}} [\sqrt{1-\zeta ^{2}}\frac{s+\zeta \omega _{n}}{(s+\zeta \omega _{n})^{2}+\omega_{d}^{2}} +\zeta \frac{\omega _{d}}{(s+\zeta \omega _{n})^{2}+\omega _{d}^{2}}]$

$\Rightarrow Y(s) = \frac{1}{s} - \frac{1}{\sqrt{1-\zeta ^{2}}} [sin\beta \frac{s+\zeta \omega _{n}}{(s+\zeta \omega _{n})^{2}+\omega _{d}^{2}} + cos\beta \frac{\omega _{d}}{(s+\zeta \omega _{n})^{2}+\omega _{d}^{2}}]$

其中， $\omega _{d} = \omega _{n}\sqrt{1-\zeta ^{2}}$ ， $sin\beta = \sqrt{1-\zeta ^{2}}$ ， $cos\beta = \zeta$ 。

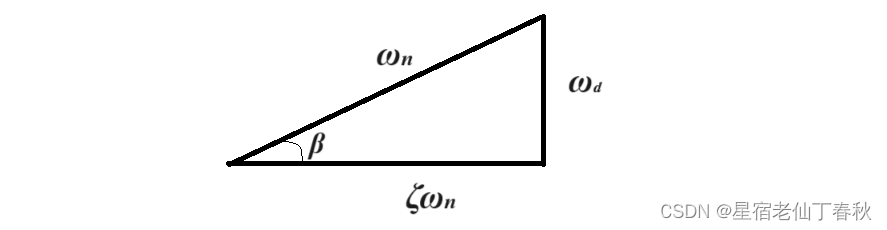
图1. 角β

对频域解 $Y(s)$ 做拉普拉斯逆变换得到时域解为：

$y(t) = L^{-1}[Y(s)]$

$\Rightarrow y(t) = 1 - [\frac{1}{\sqrt{1 - \zeta ^{2}}}\cdot e^{-\zeta \omega _{n}t} \cdot sin(\omega _{n} \sqrt{1-\zeta ^{2}} \cdot t+ arccos\zeta )]$

从时域解来分析这个系统的输出结果是否是稳定的，把该结果进行拆分，可拆分为两个核心的部分：

(1) 第一个核心部分： $e^{-\zeta \omega _{n} t}$

(2) 第二个核心部分： $sin(\omega _{n} \sqrt{1-\zeta ^{2}} \cdot t + arccos\zeta )$

并且，注意：闭环极点为 $s_{1,2} = -\zeta \omega _{n} \pm j\omega _{n} \sqrt{1-\zeta ^{2}}$

第一个核心部分是一个指数函数，在 $f(x) = e^{ax}$ 中，当 $a>0$ 时，函数单调递增，当 $a<0$ 时，函数单调递减，如下图2所示。

如果 $a = - \zeta \omega _{n} < 0$ ，即系统特征方程得根的实部为负数（闭环极点的实部为负数，位于复平面的左半平面），则，当 $t\rightarrow \infty$ 时，第一个核心部分 $e^{-\zeta \omega _{n} t} \rightarrow 0$ ；第二个核心部分 $sin(\omega _{n} \sqrt{1-\zeta ^{2}} \cdot t+ arccos\zeta )$ 是一个正弦函数，形式为 $sin(\omega t + \psi )$ 。

两个核心部分相乘的形式为：

$e^{-\zeta \omega _{n}t} \cdot sin(\omega _{n} t \sqrt{1-\zeta ^{2}} + arccos\zeta ) = A(t)\cdot sin(\omega t + \psi )$

$A(t) = e^{-\zeta \omega _{n} t}$ 作为正弦函数 $sin(\omega t + \psi )$ 的幅值。

从以上分析可知， $A(t) = e^{-\zeta \omega _{n} t}$ 随着时间 $t$ 的增大而逐渐减小，并且，在 $t\rightarrow \infty$ 时， $A(t)\rightarrow 0$ ，因此，乘积的结果是：一个幅值随时间增大而不断减小的正弦函数，如图 3 所示。至于最后一部分 $\frac{1}{\sqrt{1-\zeta ^{2}}}$ 是一个固定的系数，也就不需要再分析了，按比例缩放就行。整个输出结果是，当 $t\rightarrow \infty$ 时， $e^{-\zeta \omega _{n}t} \cdot sin(\omega _{n} t \sqrt{1-\zeta ^{2}} + arccos\zeta ) \rightarrow 0$ ， $y(t) = 1$ ，得到的是一个稳定的输出结果。

图2. 指数函数 $f(x) = e^{ax}$

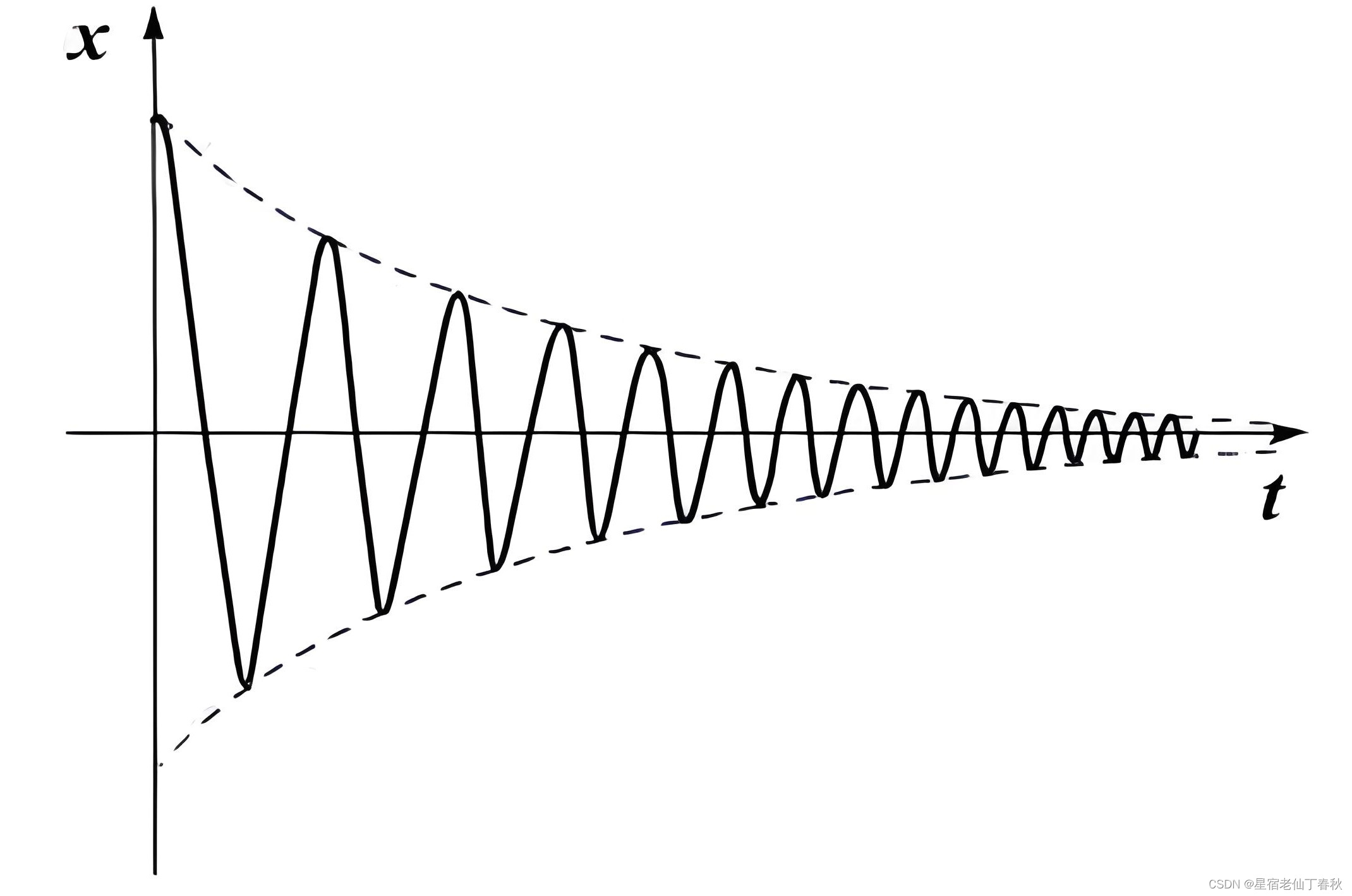
图3. 幅值按照指数规律逐渐减小的余弦函数

三. 从二阶系统到任意阶高阶系统

3.1 先看看一阶系统的时域解

在一阶系统的输入为单位阶跃信号 $R(s) = \frac{1}{s}$ 时，

一阶系统闭环传递函数： $\Phi (s) = \frac{Y(s)}{R(s)} = \frac{1}{Ts+1}$

其极点为： $s = - \frac{1}{T}$

代入阶跃输入 $R(s) = \frac{1}{s}$ 有：

$\Rightarrow Y(s) = \frac{1}{Ts+1} \cdot \frac{1}{s}$

对频域解 $Y(s)$ 进行拉普拉斯逆变换得时域解：

$y(t) = L^{-1}[Y(s)]$

$\Rightarrow y(t) = 1 - e^{-\frac{t}{T}}$

从该结果中可以看出，如果极点 $s = - \frac{1}{T}$ 的实部 $-\frac{1}{T} < 0$ ，那么，当 $t \rightarrow \infty$ 时，指数函数 $e^{-\frac{t}{T}} \rightarrow 0$ ，系统有稳定得输出结果。

3.2 再来看看三阶系统的时域解

当输入信号为单位阶跃信号 $R(s) = \frac{1}{s}$ 时，有

三阶系统得传递函数为：

$\Phi (s) = \frac{Y(s)}{R(s)} = \frac{\omega _{n}^{2}}{(s^{2} + 2\zeta \omega _{n}s + \omega _{n}^{2})(Ts+1)}$

其时域解为：

$y(t) = 1 - [\frac{1}{\zeta ^{2}\beta (\beta -2)+1}\cdot e^{-\frac{1}{T}t}] - [\frac{\zeta \beta }{\sqrt{1-\zeta ^{2}}\cdot \sqrt{\zeta ^{2}\beta (\beta -2)+1}}e^{-\zeta \omega _{n}t}\cdot sin(\omega _{d}t+\theta )]$

其中， $\beta = \frac{\frac{1}{T}}{\zeta \omega _{n}}$ ， $\omega _{d} = \omega _{n}\sqrt{1-\zeta ^{2}}$ ， $\theta = tan^{-1}\frac{\zeta (\beta -2)\sqrt{1-\zeta ^{2}}}{\zeta ^{2}(\beta -2)+1}$ 。

三阶系统的解是一个一阶系统形式的解和一个二级系统形式的解的组合，而，一二阶系统的解是否为稳定的输出结果已经讨论过，不在需要讨论。

3.3 最后看看任意阶高阶系统

一句话：高阶系统是由低阶系统级联而成的，一个n阶的传递函数可以分解为最低一阶或二阶传递函数的求和。一阶，二阶系统的解是否是稳定输出结果已经分别讨论过，高阶系统的解无非是把多个一阶系统形式的解和多个二阶系统形式的解进行叠加，直接把这样类型的输出信号的波形相叠加即可。

四. 扩展：理解主导极点

主导极点是指在系统的所有闭环极点中，距离虚轴最近且周围没有其他闭环零点的极点，主导极点对系统的动态性能影响最大，起着决定性的主导作用。

为什么主导极点是距离虚轴最近的且周围没有其他闭环零点的极点？为什么主导极点对系统的动态性能影响最大？

假设有一个稳定系统，这里来考察一下为什么主导极点需要距离虚轴最近，至于第二个限制条件周围没有其他闭环零点暂时不考虑。

从以上分析可以知道，闭环极点的实部在时域响应的解中，充当了指数函数 $y = e^{ax}$ 的系数 $a$ 的角色，当闭环极点越靠近虚轴，也就是，对于一阶系统， $a = -\frac{1}{T} < 0$ 约接近于0，对于二阶系统， $a = -\zeta \omega _{n} < 0$ 越接近于0。

把这个结论放到指数函数中，即， $y = e^{-|a|x}$ 中，可知， $|a|$ 越接近于0，意味着该指数函数的函数值减小速度越慢。

反过来看看，如果 $|a|$ 比较大意味这什么？它意味着，函数值随着 $x$ 的增大将很快衰减到0附近，并且， $|a|$ 越大，函数值衰减到0附近的速度越快。那些越快衰减到0附近的成份当然对系统的动态性能影响越小，那些衰减慢的成份当然是使系统输出达到稳定所需要时间拉长以及其他动态性能降低的罪魁祸首。衰减慢的成份和衰减快的成份相比，在自变量 $x$ （对应于控制系统中的自变量时间 $t$ ）取相同值时，拥有更大的输出分量 $y$ ，在进行叠加后，在总输出结果中占有更大的比例，对输出的结果影响更大，这就导致了主导极点对系统的动态性能影响最大。就好像 $100+2+1=103$ 的结果103主要取决于100这个分量。

星宿老仙丁春秋

关注

11
点赞
踩
16

收藏

觉得还不错? 一键收藏
1
评论
为什么传递函数的闭环极点都在复平面的左半平面的系统就是稳定系统？

对于一个自动控制系统，首先要进行不是确定系统的性能指标能否满足要求，而是系统是否稳定，通常，只有稳定的自动控制系统才是人们需要的有价值的系统。判断一个系统是否是稳定系统的原则是：系统的都具有负实部，所有的闭环极点都位于ｓ平面的左半部分的系统是稳定系统。
复制链接

扫一扫