GNSS/INS组合导航（五）：惯性导航参数建模

两种建模方法：动力学建模（Dynamic Modeling）、运动学建模（Kinematic Modeling）

动力学建模： 对力与相互作用引起的运动进行描述。表现一个物理系统对另一个物理系统的影响。例如：牛顿第二运动定律，表达了由力模型：F{r, v, t} 引起的运动变化。其中r是位置向量，v是速度向量，这些被称为状态向量，时间t是一个自变量。
F{r, v, t} = ma= mv’= mr’’
r( t) =r( t, b, c) 其中c，b为常数
r( 0) =r( 0, b, c)
v( 0) =v( 0, b, c)

地球的自转和描述卫星绕地球运行的运动通常使用动力学建模。但不适用于物体在地球表面的运动。

运动学建模：运动学建模常用于对运动物体进行动力学建模不切实际的情况。它研究的是物体的运动，而不考虑其质量或作用于其上的力，从而排除了力模型。在运动学建模中，物体的运动完全是根据位置、速度和加速度测量值来确定的，这些测量值统称为可观测值。
根据可观测到的结果，位置矢量可表示为：r( t)={ x( t ) , y( t ) , z ( t ) }
速度矢量为：
 

 加速度矢量为：

1.INS Mechanization

Mechanization：是把IMU的输出转换成位置、速度和姿态信息的过程。IMU输出包括陀螺仪测量的三轴的旋转速率和加速度计测量的三轴加速度。系统框图如下所示：

 1.1 惯性系（i-frame）作为参考系

 

加速度计的输出称为 比力f（除了重力以外的力）：

 

 其中，f为比力，a为载体测得的加速度，g为 重力矢量。测量值是在载体系（b）获得的，通常假定传感器的三轴与载体系重合，此时测量值可以通过3x3的旋转矩阵Rib变换到惯性系上（从b系变换到i系）：

 

i系下的Mechanization方程可归结为： 

 ri =[ xi yi zi ] 是i系的三维位置矢量；vi =[ vxi vyi vzi ] 是i系的三维速度矢量;

Wib为陀螺仪输出的角速度，旋转矩阵的导数 = 旋转矩阵*角速度的反对称矩阵

 1.2 地心地固坐标系（ECEF） 作为参考系

 

e系下的Mechanization方程可归结为：

 其中输入为加速度计测量的速度和陀螺仪测量的转速。输出是位置向量r，速度向量v和欧拉角，都在e坐标系中表示。

1.3 当地水平坐标系（local-level frame）作为参考系

local-level frame是最常用的坐标系，使用当地坐标系的优点：
a. 当地坐标系可以直观地表现地球表面用户的导航状态。
b. 由于I-frame的轴线与当地的东、北、天方向对齐，所以在当地坐标系中求解时，可以通过方程的输出处获得姿态角(俯仰、横滚和方位角)
c. 水平(E-N)平面上导航参数的计算误差受舒勒效应的约束。
d. 舒勒效应规定了水平面元件的惯性系统误差耦合产生舒勒回路，这些误差以舒勒频率的1/5,000 Hz振荡。

 

2. 旋转矩阵的参数化

最常用的三种方法是欧拉角法、方向余弦法和四元数法。
欧拉角只需要三个独立的参数。方向余弦（旋转矩阵）有9个参数，其中6个是独立的。这两种方法在计算上较为复杂，不适用于实时的计算，并且欧拉角容易产生奇异点。旋转矩阵的求解是不封闭的。因此，参数化转换矩阵最有效的方法是使用四元数方法。
 

2.1求解旋转矩阵

 从b系到k系的旋转矩阵随时间的变化率表示为：

其中，omga是传感器测量角速率[wx,wy,wz]的反对称矩阵： 

 

 求旋转矩阵的导数 需要求解9个微分方程，才能从角速度数据中得到变换矩阵。
现在讨论这个方程的一个封闭解。假设角速度w在很小的时间间隔内是恒定的。则旋转角度的增量为：

 

 根据推导式，可以将旋转矩阵写成递归的形式：

 省略中间推导过程，最终得到以下结果：

 

2.2求解四元数

欧拉定理指出,刚体相对于参考系的旋转，可以表示刚体绕固定轴旋转一个角度。

上图表示了一个角轴旋转，其中矢量n为旋转轴，theta为绕n旋转的角度。三个角 alpha、beta、gama定义了单位矢量旋转轴n的方向。四元数可通过角轴表述为： 

四元数由一个实部与三个虚部构成，根据上式可知，四元数通过三个独立的分量便足以描述刚体的旋转，并且存在以下约束：

 

 四元数的导数为：

 

 将其表示为递推式：

 令：

则：

 

2.3 数值积分法求解

在旋转速率较低的情况下，可以采用数值积分的方法求解，即：

 

 相当于对递推结果进行一阶近似。

2.4 旋转矩阵与四元数的相互转换

若已知四元数 q=[ q1,q2,q3,q4],则可通过下式得到旋转矩阵：

同样，在确定旋转矩阵后，也可将其转化为四元数（对准过程中测量的姿态角确定初始旋转矩阵后，计算四元数的初始值）：

 

2.5 旋转矩阵与欧拉角的相互转换

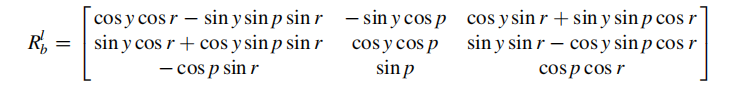
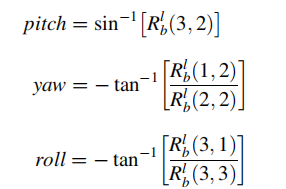
2.6 旋转矩阵、欧拉角、四元数

四元数方法的优点：
a. 四元数只需要求解4分方程（4个自由度），而旋转矩阵需要求解6个方程（6个自由度）。
b. 四元数避免了使用欧拉角时可能出现的奇异性问题。欧拉角奇异性问题
c. 四元数计算相对简单

四元数方法的缺点：
结果中存在非线性项以及需要在计算周期中重新正规化。

以下罗列使用欧拉角、旋转矩阵、四元数三种方法对旋转进行参数化的优点和缺点：
 

方法	优点	缺点
欧拉角	3个自由度（仅需3个方程即可求解）、可直接求出Roll、Pitch、Yaw	非线性微分方程、角度正负90°时存在奇异性
旋转矩阵	非奇异性、线性微分方程	6个自由度、计算复杂、无法直接求出欧拉角
四元数	4个自由度、非奇异性、仅需要3个微分方程	无法直接求出欧拉角、初始化时需要借助欧拉角

 
 

3.当地坐标系（l-frame）的导航参数求解步骤

a.陀螺仪中获得的旋转速度(wx，wy ，wz)与加速度计测得的加速度（ fx，fy，fz）构成IMU输出。
b.根据加表与陀螺仪计算俯仰，横摇和方位(p,r, A)的姿态角
第四章中【通过加速度测量的比力，可以计算出初始姿态角中的pitch和roll，若角速率(wx，wy ，wz)可以感知地球自转则可以求得航向角】。由此得到b系相对于local系的旋转矩阵Rlb。
c.使用前一步计算得到的Rlb，将b系中的比力转化为local系中的比力，得到东北天坐标系下的加速度为：(fe, fn, fu)。
d.加速度计除了比力外，测量值中还包含地球引力与科氏力，因此需要除去这两个影响因素。
e.通过对东北天坐标系下的加速度 (fe, fn, fu)进行积分，计算东、北、天的速度(Ve, Vn, Vu)。
f.通过对东、北、天的速度(Ve, Vn, Vu)进行积分，计算 大地坐标系下的位置（纬度，经度，高度）。