手撕永磁同步电机：foc（clark、park、ipark）变换、电机数学模型解耦过程推导

---

前言

此文是对电机模型由定子空间位置（三相坐标轴）到复平面（两相坐标轴）再到dq坐标轴（旋转坐标轴）整个解耦过程的公式推导并由此得到foc（clark、park、ipark）变换。望君多多指点；

一、建立数学模型的作用？

先熟悉一下数学模型；
1.电压方程：关于电压跟电流非线性的关系函数；
2.磁链方程：电流跟磁链的关系属于线性关系；如果有电机转子磁链跟定子电感可以根据电流得出磁链关系（定子电感主要由磁极磁导率、大小决定）；
3.转矩方程：以磁链为中间变量电流跟力矩的线性关系
4.运动方程：力矩跟转速之间的非线性关系函数；

如上图：
速度环：根据运动方程我们就能知道我们如果想要控制转速或者位置，需要对力矩进行控制；因为力矩跟转速是非线性系统，所以在这就引入pi控制器也就是我们说的速度环调节器，属于一个控制系统了，通过已知的固定参数，并调节系统带宽最终达到转速的控制；一些摩擦系数转动惯量可以通过自整定算法计算，但往往会存在偏差，最终还需要实际调节（试凑法）
电流环：因为力矩跟电流是属于线性关系，所以只需要考虑电流跟电压的关系，也就是所谓的电流环，这里也是因为电压跟电流的二阶阻尼系统所以引入pi控制器，通过调节电压的大小进而得到目标电流；（电流环的带宽只跟电阻、电感、转子磁链等电机本体参数有关）

二、数学模型

1.三相坐标系下数学模型

1.电压方程

2.磁链方程

其中：La为a相线圈自感、Lab为ab相线圈之间的互感
如上图为三相坐标系下的电压方程以及磁链方程；耦合行非常强，这也就是我们引进foc的目的，对强耦合的数学模型解耦由原本的控制交流变为dq轴的直流控制；

2.复平面的数学模型（两相坐标）

1.复平面跟极坐标

上述是依据欧拉公式为基础，根据实际的三相定子线圈以及转子空间位置推导的极坐标向量

2.极坐标下的电压方程

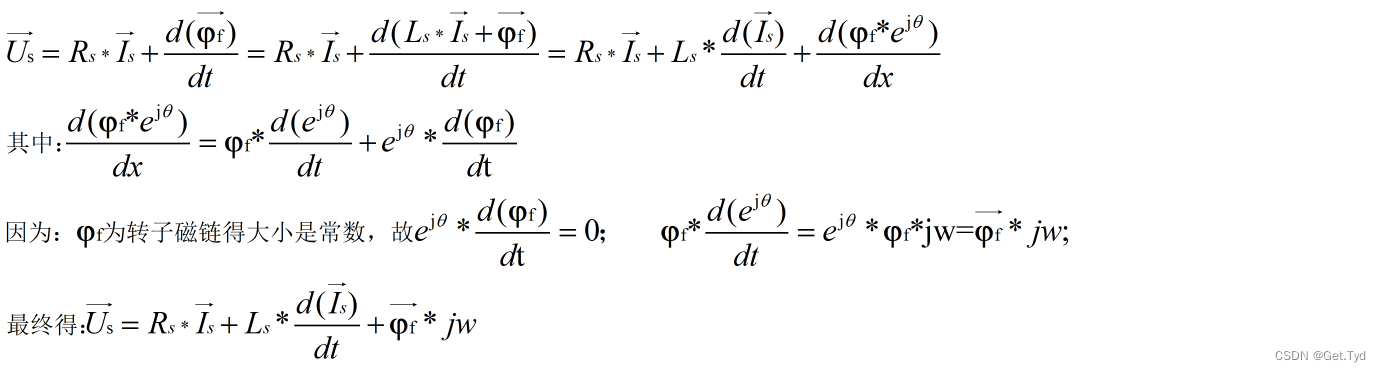
Ls：电感跟磁导成比例关系，可以根据这点推出Ls；如果转子为隐极(SPMSM)的话气隙磁场跟转子磁极磁导率一致，故整个转子跟定子间的磁阻大小均匀分布，得Ls=Ld=Lq=1/2线电感；如果为凸极机（IPMSM）得话一般电机图纸都会给出实际得dq轴电感；
Rs=相电阻=1/2线电阻；
3.极坐标下磁链方程

3.dq轴坐标数学模型（旋转坐标）

1.dq坐标跟极坐标

如上图所示，将dq轴与的αβ坐标轴标在同一坐标系：把d轴作为一个矢量，在αβ坐标轴的矢量向量就为|d|*e指数jθ，由此可得：极坐标跟旋转坐标的关系：

2.dq坐标下得电压方程推导

3.dq坐标轴下的磁链方程

4.转矩方程

5运动方程

4.clark、park推导

1.clark推导
以电压变换为例

综上所述：

到这就会有人提出这跟书中或者其他地方不一样呢？
正常应该是：

其中：k=2/3则为等幅值变换k=根号2/3为恒功率变换
个人理解原因为如下：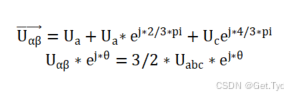

如上公式中变换前后幅值基础对于前者不一致，但是在svpwm输出是期望电压幅值为以Uabc为基础实际输出，但是clark变换中是以电流为基础，如果乘2/3同样也就为以I abc为基础，这样就能保证电机数据模型准确。

2.park推导

总结