李雅普诺夫稳定

0. 参考文献

【１】https://zhuanlan.zhihu.com/p/58738073
这个文章写的已经非常透彻了，没什么好说的，本文全文摘抄

1. 什么是平衡点

看一个倒立摆的例子：

这个倒立摆的状态方程第一行，没什么好说的，状态量就角度和角速度。
第二行，对小球进行受力平衡分析把$J_t$乘过去就比较容易看出来了

注意上面这一段，将输入设成０，也就是０输入系统，会自然进行摆动
因为很多量都是常数，所以作者自己造了一个火箭：


这里其实也可以拿手画，就是比较复杂



上面关于平衡点的解释还是非常直观的，状态方程左侧都是状态的导数，右侧都是状态的函数，我们只要在图上选一个状态点，根据状态点，求出在该状态下的，状态的导数，就是那个图上的箭头。同样的，我们要找平衡点，就是让导数等于零，然后取求解状态

上面这一段，还有下面的描述是不是有点问题啊？不是竖直放置不稳定，是竖直向上放置不稳定，竖直向下放置稳定
下面这一段中不是火箭水平躺着，是火箭竖直向下

2. 什么是李雅普诺夫稳定

李雅普诺夫稳定性理论研究的是在扰动下平衡点的稳定性问题。

受到扰动，停留在“附近”

受到扰动，“收敛”到平衡点

受到“任何”扰动，“收敛”到平衡点

受到扰动，偏离平衡点

2.1 李雅普诺夫稳定

这是一个线性系统

真的这么容易吗，看来又要复习了

下面这个关键的来了



上面这个例子是里面的向外走，外面的向里走，共同走到同一个圈上

2.2 渐进稳定

2.3 大范围渐进稳定

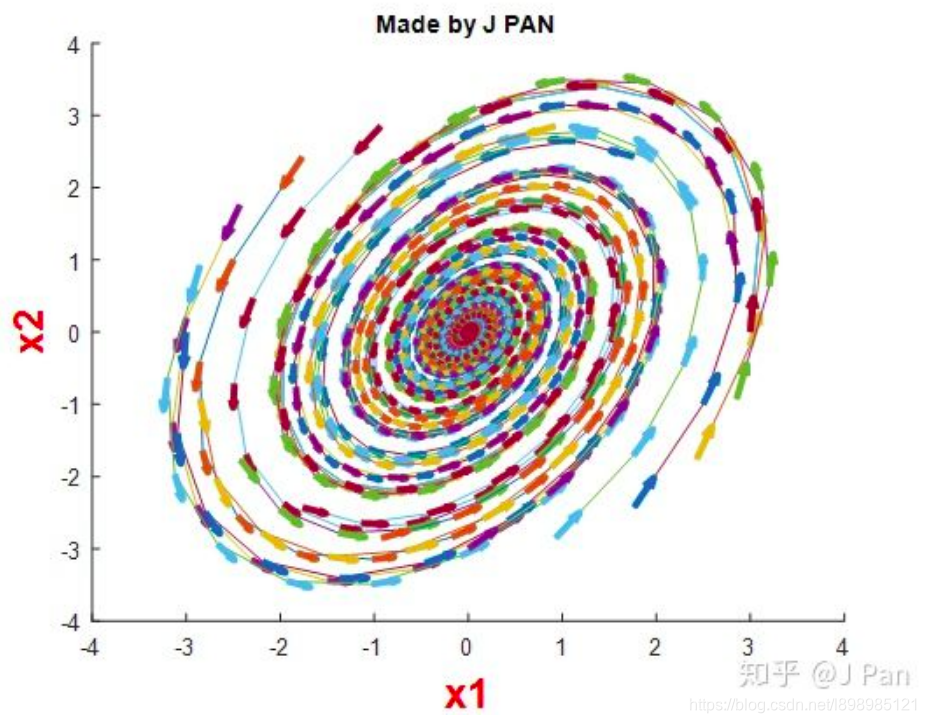
注意下面这两个结论

2.4 不稳定

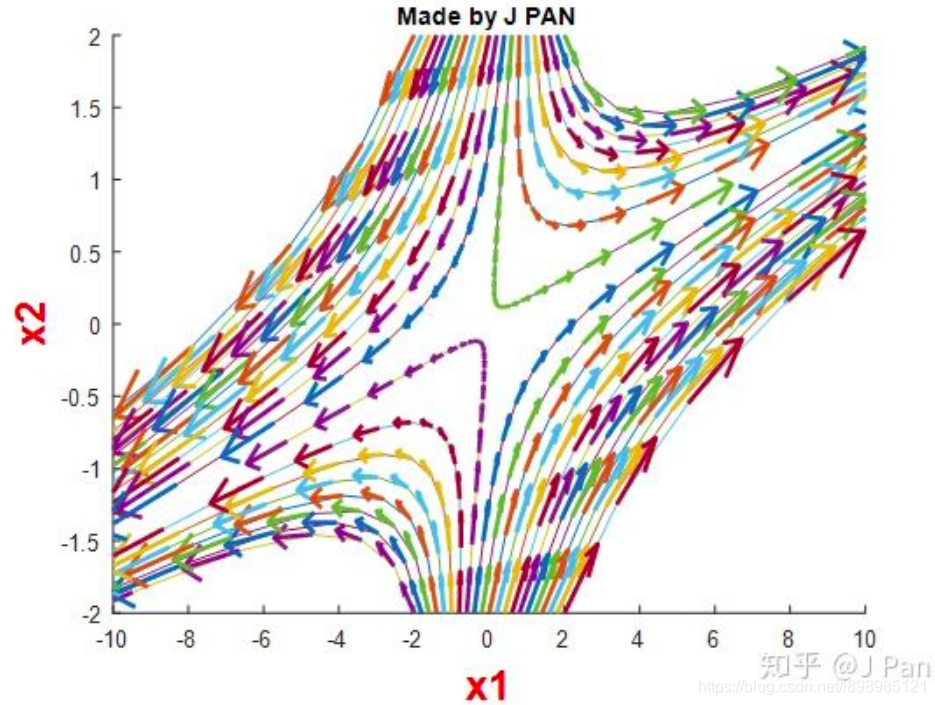
3. 李雅普诺夫第一法

在平衡点附近线性化

4. 李雅普诺夫第二法

注意这个标量函数的一些条件：首先这个标量函数是状态量的函数，并且在x!=0时是非负的，如果这个标量函数对时间的求导小于等于０。那么就是李雅普诺夫稳定的

注意这个标量函数，要我们自己取找才行，并且找到一个就行，不用找很多



注意看上面，这个李雅普诺夫函数是我们自己选的，然后自己去试试导数行不行