DS之MDS：MDS(Multidimensional Scaling)多维尺度降维算法的简介、使用方法、案例应用之详细攻略

DS之MDS：MDS(Multidimensional Scaling)多维尺度降维算法的简介、使用方法、案例应用之详细攻略

目录

MDS的简介

MDS(Multidimensional Scaling)降维算法的概述

MDS的案例应用

1、使用MDS对高维数据进行降维并在3D空间中可视化

---

MDS的简介

MDS(Multidimensional Scaling)降维算法的概述

简介	多维尺度（Multidimensional scaling，缩写MDS，又译“多维标度”）也称作“相似度结构分析”（Similarity structure analysis），属于多重变量分析的方法之一，是社会学、数量心理学、市场营销等统计实证分析的常用方法。 MDS是一种多维尺度分析方法，用于将高维数据映射到低维空间中，以便进行可视化或降维。 MDS是一种简单易用而且结果可解释的降维技术，通过数据的相似度或相关性矩阵可以得到直观的二维或三维视图，非常适合用于数据可视化和结构分析。但是对大数据集效果可能会受限，并可能产生一定的失真，需视具体应用场景选择。
目标	MDS的目标是保持数据点之间的距离关系，尽可能地在低维空间中保持高维数据的结构。
实现思路	初始化→计算低维距离→利于Stress 密度比较差距→持续优化坐标来降低Stress 密度 1)、初始化低维空间中的样本坐标(通常随机初始化)； 2)、计算低维空间中样本间的距离矩阵； 3)、与原始高维距离矩阵比较，计算差距(通常使用 Stress 密度)； 4)、不断优化低维样本坐标，不断降低 Stress 密度； 5)、迭代到满足条件(Stress 密度足够小或达到最大迭代次数)后，得到最终的低维坐标；
特点	非参数估计、矩阵分解、无监督、线性变换、最大化保留距离关系、全局结构。 (1)、保持结构/相似性：MDS旨在保持数据点之间的相似性或距离关系，尽可能地在低维空间中保留原始数据的结构。可以保留数据之间的度量关系，如距离、相似度等。通过低维空间的距离来反映高维空间的数据关系。 (2)、非线性映射：MDS可以进行非线性映射，因此它可以处理复杂的数据结构和非线性关系。 (3)、可解释性：MDS提供了对数据的可解释性，可以通过可视化在低维空间中观察数据点的位置和相对位置。 (4)、非参数方法：不需要对数据做任何假设，直接从距离或相似度矩阵中估计数据的坐标。
应用场景	MDS是一种用于分析和可视化数据的方法，它试图在低维空间中保持原始数据的距离或相似性关系。 1、数据可视化：MDS可以将高维数据映射到二维或三维空间，以便进行可视化呈现。它在探索性数据分析和数据展示中非常有用，便于人们理解复杂的数据结构。 2、相似性分析：MDS可以用于分析物品、概念或观点之间的相似性关系。例如，在市场调研中，可以使用MDS来分析消费者对产品的相似性评价。 3、空间分布分析：MDS可以用于分析地理位置或城市之间的相似性和距离关系。这对于城市规划、地理研究和社会网络分析等领域很有意义。
优缺点	(1)、简单直观，易于理解和解释。 (2)、结果稳定可靠。
	(1)、失真可能会产生较大，特别是在高维到低维的映射中。 (2)、难以应用于大规模数据集，计算复杂度较高。
应用案例	社会调查和心理学：用于判断人们对对象或概念的感知结构。 文本分析：可以判断词语之间的语义相关性和结构。 产品定位：在市场研究中，可以使用MDS来分析不同产品或品牌之间的相似性关系，从而帮助企业了解消费者的购买偏好和市场定位。品牌间的竞争关系分析、顾客对不同产品的态度结构研究等。 社会网络分析：MDS可以用于分析社会网络中的人际关系，将个体或团体之间的联系映射到低维空间，以便可视化和研究。 地理空间分析：MDS可以用于分析城市之间的空间距离和相似性关系，从而揭示城市之间的空间结构和相互作用模式。

MDS的案例应用

1、使用MDS对高维数据进行降维并在3D空间中可视化

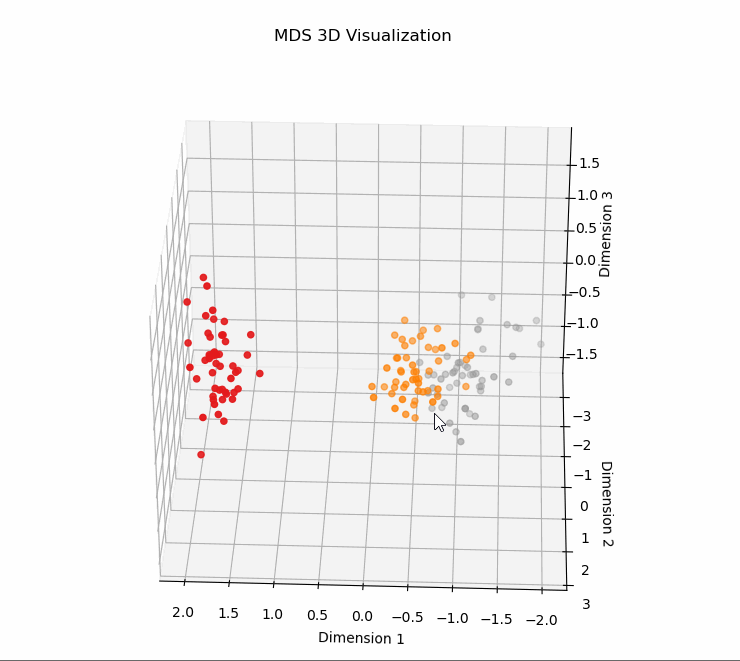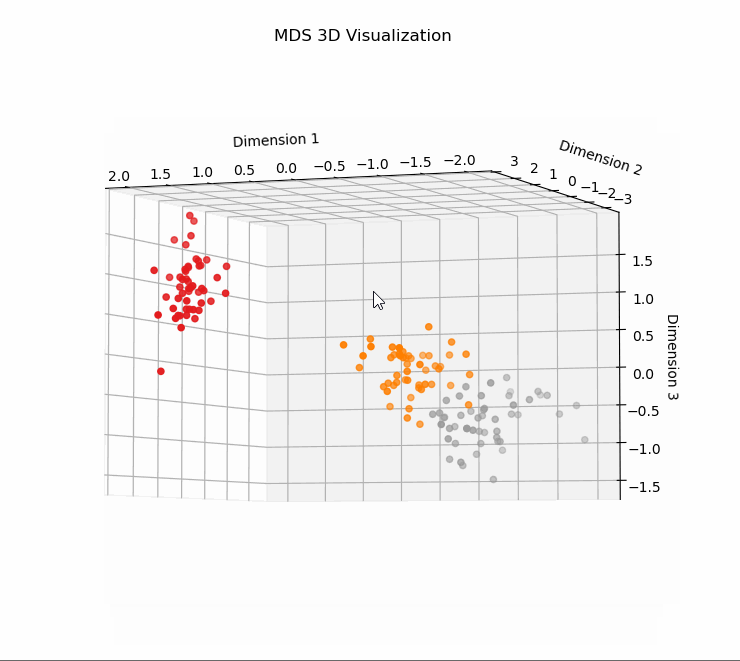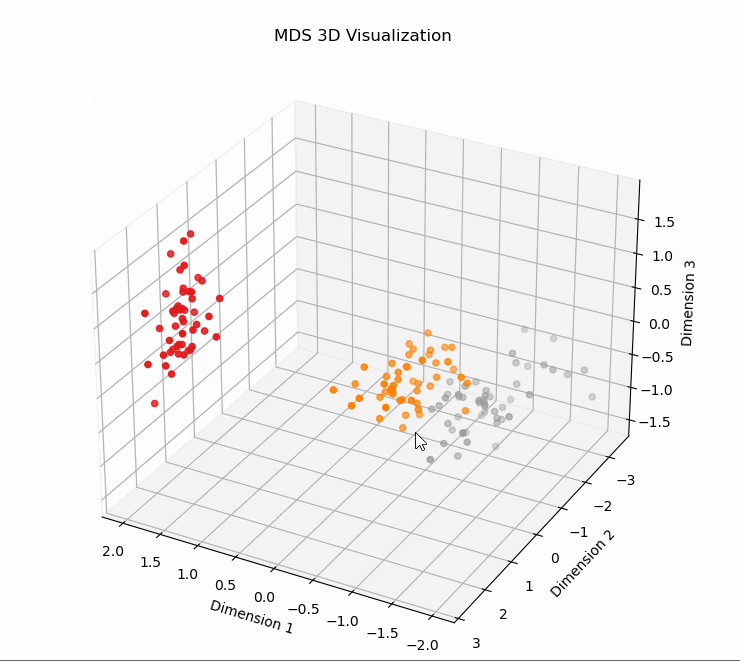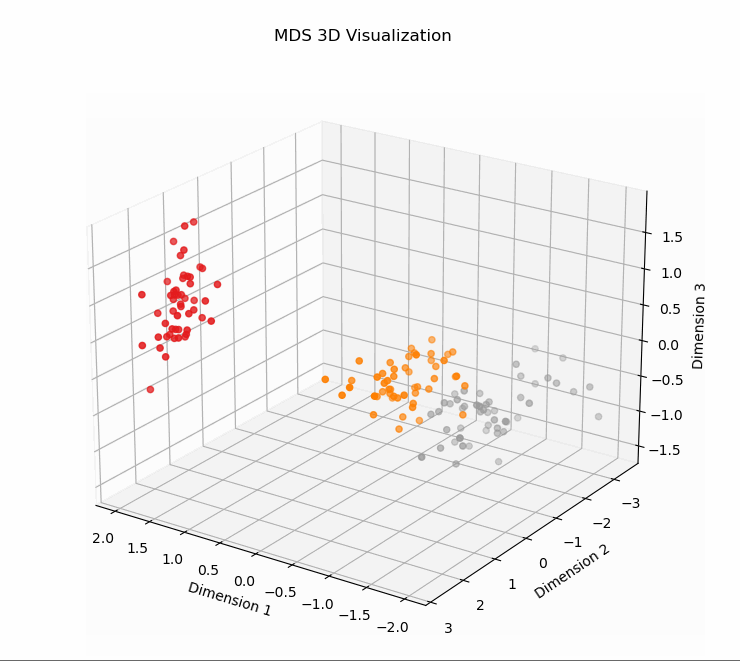
# 使用MDS对高维数据进行降维并在3D空间中可视化
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_iris
from sklearn.manifold import MDS

# 加载示例数据集（鸢尾花数据集）
iris = load_iris()
X = iris.data
y = iris.target

# 使用MDS进行降维
mds = MDS(n_components=3)
X_mds = mds.fit_transform(X)

# 创建3D可视化图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制散点图
ax.scatter(X_mds[:, 0], X_mds[:, 1], X_mds[:, 2], c=y, cmap='Set1')

ax.set_xlabel('Dimension 1')
ax.set_ylabel('Dimension 2')
ax.set_zlabel('Dimension 3')
ax.set_title('MDS 3D Visualization')

plt.show()