概率机器人笔记(4)：粒子滤波的简单理解与推导

1.粒子滤波基本过程

(1) 问题描述

当状态转移模型和测量模型不是线性时，后验概率$bel(x_t)$不再服从高斯分布，作为贝叶斯滤波的另一种非参数实现，粒子滤波采用从后验得到的有限个随机状态样本来表示后验分布$bel(x_t)$。后验的样本${\chi }_t:=x_t^{[1]},x_t^{[2]},x_t^{[3]},\cdot \cdot \cdot ,x_t^{[M]}$，每一个粒子都代表着一种可能的状态假设。

如上图，状态假设$x_t$在粒子集中的可能性与贝叶斯滤波的后验分布$bel(x_t)$成比例：$$x_t^{[m]}\sim p(x_t|z_{1:t},u_{1:t})$$

(2) 基本算法

1：${\chi }_t,{\overline{\chi }}_t$先设为空集，${\chi }_t$为最终输出的粒子集，${\overline{\chi }}_t$为暂时粒子集
2：对每一个粒子都进行下面的操作
3：从简单分布$\pi (x)$按照其概率分布采样出一个粒子
4：求出该粒子对应的权重
5：将该粒子添加到暂时粒子集${\overline{\chi }}_t$中
6：采集、计算权重结束，得到了$J$个暂时的样本，虽然赋予了权重，但是粒子的分布还是按照简单分布$\pi (x)$来的。
7：对每一个粒子都进行下面的操作
8：以计算的权重为概率从暂时数据集${\overline{\chi }}_t$中抽取粒子
9：将抽取的粒子放入最终粒子集${\chi }_t$中
10：重采样结束，得到$J$个最终的样本，作为后验概率的表示
分析完程序的整个运行过程之后，难免会有疑问：

• 如何从简单分布$\pi (x)$中取样？
• 如何按照权重进行重采样？
• 在机器人定位中，简单分布和权重是怎么表示的呢？

2.采样Sampling

(1) 蒙特卡洛方法

蒙特卡洛方法也叫统计模拟方法，是用随机数来进行计算机模拟的方法。在对某种随机分布进行分析时，往往需要对分布的数字特征(这里以均值为例说明)进行求解分析，当问题比较简单时，我们可以利用均值的定义以及性质进行求解。但是当问题变得复杂，比如随机变量的维数增多，我们很难按照以前的求解方式进行求解。蒙特卡洛方法通过对模型或过程的观察或抽样试验来计算这些参数或数字特征，最后给出所求解的近似值。
根据大数定律，简单理解就是随着某个独立重复实验次数的增多，某个事件发生的频率依概率收敛到该事件的概率。比如当我们需要计算连续型随机变量$X\sim p(x)$对于函数$f(X)$的均值时，$$E[f(X)]=\int f(x)p(x)dx\approx \frac{1}{n}\sum _{i=1}^{n}f(x_i)$$
根据上面的公式，我们从$p(x)$中采样$x_1,x_2,\cdot \cdot \cdot ,x_n$，当$n->\infty$时，得到的结果越趋近于真正的均值。在实际应用时，我们往往没有必要知道真正的均值是多少，只要我们通过蒙特卡洛方法在计算机上模拟出的值在我们期望的误差范围之内即可。
那么，如何从$p(x)$中进行采样呢？
一般来说，蒙特卡洛方法分为物理模拟和数学模拟两种，这里只讨论数学模拟。参考文献1,2给出了蒙特卡洛采样的思想，按一定的概率分布从中获取大量样本，用于计算函数在样本的概率分布上的期望。其中最关键的一个步骤就是如何按照指定的概率分布p进行样本采样，首先把这个概率分布写成累计概率分布的形式，就是从pdf写成cdf，然后在[0,1]上均匀取随机数(因为计算机只能取均匀随机数)，假如我们取到了0.3，那么在cdf上cdf(x0)=0.3的点x0就是我们依据上述概率分布取得的随机点。但是当随机分布很复杂的时候，我们很难求出累积分布函数，所以采样也就无从谈起了。

(2) 重要性采样（Importance Sampling）

很多情况下，我们很难从一个分布中采样，即使这个分布的概率分布函数已知，但是累积分布函数也可能会比较难求。比如，我们想求：$$E[f(x)]=\int f(x)p(x)dx,x\sim p(x)$$由于我们比较难从$p(x)$中采样，因此引入另一个已知的简单的分布$q(x)$：$$E[f(x)]=\int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=\int g(x)q(x)dx,x\sim q(x)$$其中，$p(x)$称为目标分布，$q(x)$称为建议分布，$g(x)=f(x)\frac{p(x)}{q(x)},\frac{p(x)}{q(x)}$称为权重，这么做的目的是把求$f(x)$在$p(x)$下的分布转化为求$g(x)$在$q(x)$下的分布。

可以看到，经过变换，虽然分布还是按照$q(x)$来的，在$f(x)$的部分可能采样点比较少，但是由于分配了权重，是可以表达出$E[f(x)]$来的。
重要性采样例子（来源于网络，稍有改动）：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt


#  First, let’s define function f(x) and sample distribution:
#  For simplicity reasons, here both p(x) and q(x) are normal distribution,
#  you can try to define some p(x) that is very hard to sample from.
#  In our first demonstration, let’s set two distributions close to each other
#  with similar mean(3 and 3.5) and same sigma 1:
def f_x(x):
    return 1 / (1 + np.exp(-x))


#  Now let’s define the distribution of p(x) and q(x) :
def distribution(mu=0, sigma=1):
    # return probability given a value
    distribution = stats.norm(mu, sigma)  # 默认生成均值为0，方差为1的正态分布
    return distribution


# pre-setting
n = 10000

mu_target = 0.5
sigma_target = 1
mu_appro = 3
sigma_appro = 1

p_x = distribution(mu_target, sigma_target)
q_x = distribution(mu_appro, sigma_appro)

#  Now we are able to compute the true value sampled from distribution p(x)
s = 0
for i in range(n):
    # draw a sample
    x_i = np.random.normal(mu_target, sigma_target)
    s += f_x(x_i)
print("true value", s / n)

#  where we get an estimation of ***. Now let’s sample from q(x)
#  and see how it performs:
value_list = []
for i in range(n):
    # sample from different distribution
    x_i = np.random.normal(mu_appro, sigma_appro)
    value_list.append(f_x(x_i) * (p_x.pdf(x_i) / q_x.pdf(x_i)))
value = sum(value_list) / n

print("simulate value", value)
#  Notice that here x_i is sampled from approximate distribution q(x) ,
#  and we get an estimation of 0.949 and variance 0.304.
#  See that we are able to get the estimate by sampling from a different distribution!

xs = np.linspace(-2, 8)
plt.plot(xs, p_x.pdf(xs), 'r--', label="Target PDF")
plt.plot(xs, q_x.pdf(xs), 'b--', label="Proposal PDF")


plt.show()

3.粒子滤波进行机器人定位

(1) 基本流程

4：基于状态转移概率$p(x_t|x_{t-1},u_t)$和上一时刻的粒子$x_{t-1}^{[m]}$产生预测粒子，得到粒子集代表了$\overline{bel}(x_t)$的分布。
5：重要性因子用测量的结果来更新每个粒子的权重
8-11：通过重采样，更新粒子集，使更新后的粒子符合真实的后验$bel(x_t)$

(2) 相关推导

目标分布:
假设我们有了一系列时间序列的状态样本$x_{0:t}^{[m]}=x_0^m,x_1^m,\cdot \cdot \cdot ,x_t^m$，则粒子滤波在所有状态上的后验：$$bel(x_{0:t})=p(x_{0:t}|u_{1:t},z_{1:t})$$为了避免出现积分符号计算后验$bel(x_{0:t})$而非$bel(x_t)$：$$p(x_{0:t}|u_{1:t},z_{1:t})=\eta p(z_t|x_{0:t},z_{1:t-1},u_{1:t})p(x_{0:t},z_{1:t-1},u_{1:t})$$$$=\eta p(z_t|x_0)p(x_{0:t},z_{1:t-1},u_{1:t})$$$$=\eta p(z_t|x_t)p(x_t|x_{0:t-1},z_{1:t-1},u_{1:t})p(x_{0:t-1}|z_{1:t-1},u_{1:t})$$$$=\eta p(z_t|x_t)p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})$$$$=\eta p(z_t|x_t)p(x_t|x_{t-1},u_t)bel(x_{0:t-1})$$
建议分布：$$p(x_t|x_{t-1},u_t)bel(x_{0:t-1})=p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})$$将上一次的粒子分布乘状态转移概率相当于将粒子变成了预测粒子
权重：$$w_t^{[m]}=\frac{目标分布}{建议分布}=\frac{\eta p(z_t|x_t)p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})}{p(x_t|x_{t-1},u_t)p(x_{0:t-1}|z_{1:t-1},u_{1:t-1})}$$$$=\eta p(z_t|x_t)$$通过权重的校正，预测粒子变成了可以代替后验概率的粒子
更新后验：$$bel(x_{0:t})=\eta w_t^{[m]}p(x_t|x_{t-1},u_t)bel(x_{0:t-1})$$
一点说明：
上面的程序流程图表示是将权重计算出来之后，通过归一化，将权重重新进行分配，方便按照概率重采样。另一种方式是不进行重采样，而是为每一个粒子赋予一个归一化之后的权重，并且每次循环计算时按照下面的递归进行更新：$$w_t^{[m]}=p(z_t|x_t^{[m]})w_{t-1}^{[m]}$$也称为顺序重要性采样(Sequential Importance Sampling, SIS)。顺序重要性采样往往会造成权值退化，即比重大的权值仅仅集中于少量的粒子上，大部分粒子的权重都比较低。改进的方法就是上面的重采样。权值大的粒子在下一次采样的时候多多选择，放大是按照上面蒙特卡洛的方法，通过(0,1)的均匀分布和cdf函数进行采样，重采样之后，每个粒子权重又变成一样的。

(3)低方差采样

重采样过程会引起粒子群多样性消失，造成采样误差。

与通过随机选取M个随机数选取M个粒子不同，低方差采样只选取一个随机数，便能够按照一定的比例进行采样。
2：从$[0,J^{-1}]$中随机选取一个数，作为步长
3：$c$代表粒子累加和
5-6：U均匀地按照$J^{-1}$增加
7-11：但是$c$由于各粒子权重不同，是不均匀的，因此可以按照权重大小来选取，只要$U>c$，说明当前权重太小，跳过了当前权重，选择下一个权重，同时更新$c$，下一次循环从更新之后的$c$对应的权重开始比较，如果$U<c$说明这次$c$的更新遇到了个大一点的权重粒子，仍然选择这个粒子，否则继续跳到下一个粒子，以此类推。。。
《概率机器人》中下面这幅图很形象的说明了这个原理：

4.粒子滤波实例

(1) (from udacity courses)

from math import *
import random
import numpy as np
from matplotlib import pyplot as plt

landmarks = [[20.0, 20.0], [80.0, 80.0], [20.0, 80.0], [80.0, 20.0]]  # 设置参考点
world_size = 100.0

landmark_x = np.array([20, 80, 20, 80])
landmark_y = np.array([20, 80, 80, 20])

#plt.plot(landmark_x, landmark_y, "<")
class robot:
    def __init__(self):
        self.x = random.random() * world_size
        self.y = random.random() * world_size
        self.orientation = random.random() * 2.0 * pi
        self.forward_noise = 0.0
        self.turn_noise = 0.0
        self.sense_noise = 0.0

#   设置初始坐标和方向
    def set(self, new_x, new_y, new_orientation):
        if new_x < 0 or new_x >= world_size:
            raise ValueError('X coordinate out of bound')
        if new_y < 0 or new_y >= world_size:
            raise ValueError('Y coordinate out of bound')
        if new_orientation < 0 or new_orientation >= 2 * pi:
            raise ValueError('Orientation must be in [0..2pi]')
        self.x = float(new_x)
        self.y = float(new_y)
        self.orientation = float(new_orientation)

#   设置高斯噪声
    def set_noise(self, new_f_noise, new_t_noise, new_s_noise):
        # makes it possible to change the noise parameters
        # this is often useful in particle filters
        self.forward_noise = float(new_f_noise)
        self.turn_noise = float(new_t_noise)
        self.sense_noise = float(new_s_noise)

#   传感器感知当前位置
    def sense(self):
        Z = []
        for i in range(len(landmarks)):
            dist = sqrt((self.x - landmarks[i][0]) ** 2 + (self.y - landmarks[i][1]) ** 2)
            dist += random.gauss(0.0, self.sense_noise)
            Z.append(dist)
        return Z

#   给机器人施加控制
    def move(self, turn, forward):
        if forward < 0:
            raise ValueError('Robot cant move backwards')

            # turn, and add randomness to the turning command
        orientation = self.orientation + float(turn) + random.gauss(0.0, self.turn_noise)
        orientation %= 2 * pi

        # move, and add randomness to the motion command
        dist = float(forward) + random.gauss(0.0, self.forward_noise)
        x = self.x + (cos(orientation) * dist)
        y = self.y + (sin(orientation) * dist)
        x %= world_size  # cyclic truncate
        y %= world_size

        # set particle
        res = robot()
        res.set(x, y, orientation)
        res.set_noise(self.forward_noise, self.turn_noise, self.sense_noise)
        return res

    def Gaussian(self, mu, sigma, x):

        # calculates the probability of x for 1-dim Gaussian with mean mu and var. sigma
        return exp(- ((mu - x) ** 2) / (sigma ** 2) / 2.0) / sqrt(2.0 * pi * (sigma ** 2))

    def measurement_prob(self, measurement):

        # calculates how likely a measurement should be

        prob = 1.0
        for i in range(len(landmarks)):
            dist = sqrt((self.x - landmarks[i][0]) ** 2 + (self.y - landmarks[i][1]) ** 2)
            prob *= self.Gaussian(dist, self.sense_noise, measurement[i])
        return prob

    def __repr__(self):
        return '[x=%.6s y=%.6s orient=%.6s]' % (str(self.x), str(self.y), str(self.orientation))


def eval(r, p):
    sum = 0.0
    for i in range(len(p)):  # calculate mean error
        dx = (p[i].x - r.x + (world_size / 2.0)) % world_size - (world_size / 2.0)
        dy = (p[i].y - r.y + (world_size / 2.0)) % world_size - (world_size / 2.0)
        err = sqrt(dx * dx + dy * dy)
        sum += err
    return sum / float(len(p))


myrobot = robot()  # 实际的模型
myrobot.set(0, 0, 0)

N = 1000  # 粒子数
p = []
p_x = []  # 存储所有粒子的横坐标plot
p_y = []  # 存储所有粒子的纵坐标plot
for i in range(N):  # 生成10000个粒子
    x = robot()
    x.set_noise(0.05, 0.05, 5)
    p.append(x)
T = 50  # 移动步数
for t in range(T):
    myrobot = myrobot.move(0.1, 3)
    Z = myrobot.sense()
    p2 = []
    for i in range(N):  # 所有粒子跟随原来的模型移动
        p2.append(p[i].move(0.1, 3))
    p = p2  # 随机粒子

    w = []  # 权重
    for i in range(N):  # 计算实际模型在所有粒子中的权重
        w.append(p[i].measurement_prob(Z))

    p3 = []
    index = int(random.random() * N)  # 随机选取一个权重
    beta = 0.0
    mw = max(w)

    for i in range(N):  # 重采样，类似低方差采样
        beta += beta + random.random() * 2 * mw  # 随机选取一个[0,2*mw]的跳跃值
        while beta > w[index]:  # 如果选取的权重比跳跃值小，肯定会跳到选取的下一个权重
            beta -= w[index]  # 跳到下一个的话，跳跃值也发生了变化
            index = (index + 1) % N
        p3.append(p[index])
    p = p3
    print(eval(myrobot, p))
    for i in range(N):
        p_x.append(p[i].x)
        p_y.append(p[i].y)
    partical_x = np.array(p_x)
    partical_y = np.array(p_y)
    fig = plt.figure(num=1, figsize=(15, 8), dpi=80)
    plt.plot(p_x, p_y, "*")
    ax = plt.gca()
    ax.set_xticks([0, 25, 50, 75, 100])
    ax.set_yticks([0, 25, 50, 75, 100])
    plt.show()

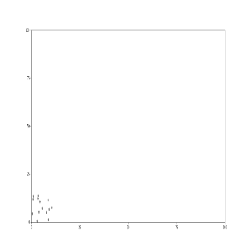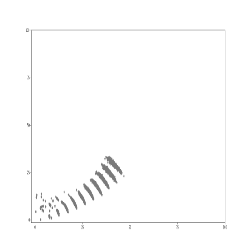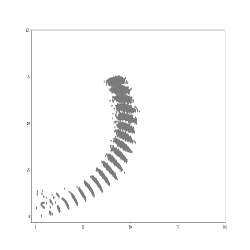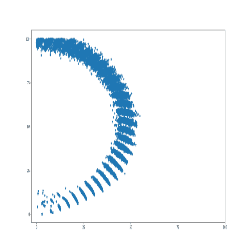
(2)(from https://www.cnblogs.com/21207-iHome/p/5237701.html)

import numpy as np
import scipy.stats
from numpy.random import uniform, randn, random
import matplotlib.pyplot as plt


def create_uniform_particles(x_range, y_range, hdg_range, N):
    particles = np.empty((N, 3))
    particles[:, 0] = uniform(x_range[0], x_range[1], size=N)
    particles[:, 1] = uniform(y_range[0], y_range[1], size=N)
    particles[:, 2] = uniform(hdg_range[0], hdg_range[1], size=N)
    particles[:, 2] %= 2 * np.pi
    return particles


def predict(particles, u, std, dt=1.):
    """ move according to control input u (heading change, velocity)
    with noise Q (std heading change, std velocity)"""

    N = len(particles)
    # update heading
    particles[:, 2] += u[0] + (randn(N) * std[0])
    particles[:, 2] %= 2 * np.pi

    # move in the (noisy) commanded direction
    dist = (u[1] * dt) + (randn(N) * std[1])
    particles[:, 0] += np.cos(particles[:, 2]) * dist
    particles[:, 1] += np.sin(particles[:, 2]) * dist


def update(particles, weights, z, R, landmarks):
    weights.fill(1.)
    for i, landmark in enumerate(landmarks):
        distance = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
        weights *= scipy.stats.norm(distance, R).pdf(z[i])

    weights += 1.e-300  # avoid round-off to zero
    weights /= sum(weights)  # normalize


def estimate(particles, weights):
    """returns mean and variance of the weighted particles"""

    pos = particles[:, 0:2]
    mean = np.average(pos, weights=weights, axis=0)
    var = np.average((pos - mean) ** 2, weights=weights, axis=0)
    return mean, var


def neff(weights):
    return 1. / np.sum(np.square(weights))


def simple_resample(particles, weights):
    N = len(particles)
    cumulative_sum = np.cumsum(weights)
    cumulative_sum[-1] = 1.  # avoid round-off error
    indexes = np.searchsorted(cumulative_sum, random(N))

    # resample according to indexes
    particles[:] = particles[indexes]
    weights[:] = weights[indexes]
    weights /= np.sum(weights)  # normalize


def run_pf(N, iters=18, sensor_std_err=0.1, xlim=(0, 20), ylim=(0, 20)):
    landmarks = np.array([[-1, 2], [5, 10], [12, 14], [18, 21]])
    NL = len(landmarks)

    # create particles and weights
    particles = create_uniform_particles((0, 20), (0, 20), (0, 2 * np.pi), N)
    weights = np.zeros(N)

    xs = []  # estimated values
    robot_pos = np.array([0., 0.])

    for x in range(iters):
        robot_pos += (1, 1)

        # distance from robot to each landmark
        zs = np.linalg.norm(landmarks - robot_pos, axis=1) + (randn(NL) * sensor_std_err)

        # move particles forward to (x+1, x+1)
        predict(particles, u=(0.00, 1.414), std=(.2, .05))

        # incorporate measurements
        update(particles, weights, z=zs, R=sensor_std_err, landmarks=landmarks)

        # resample if too few effective particles
        if neff(weights) < N / 2:
            simple_resample(particles, weights)

        # Computing the State Estimate
        mu, var = estimate(particles, weights)
        xs.append(mu)

    xs = np.array(xs)
    plt.plot(np.arange(iters + 1), 'k+')
    plt.plot(xs[:, 0], xs[:, 1], 'r.')
    plt.scatter(landmarks[:, 0], landmarks[:, 1], alpha=0.4, marker='o', c=randn(4), s=100)  # plot landmarks
    plt.legend(['Actual', 'PF'], loc=4, numpoints=1)
    plt.xlim([-2, 20])
    plt.ylim([0, 22])
    print
    'estimated position and variance:\n\t', mu, var
    plt.show()


if __name__ == '__main__':
    run_pf(N=5000)

上述代码均来源于网络，已注明地址，仅供学习参考使用
参考文献：
1.https://blog.csdn.net/yang090510118/article/details/40182915
2.https://blog.csdn.net/Dark_Scope/article/details/70992266
3.https://www.cnblogs.com/21207-iHome/p/5237701.html
4.https://blog.csdn.net/heyijia0327/article/details/40899819