视觉SLAM十四讲第3讲习题解答

1.验证旋转矩阵是正交矩阵。

解法一：

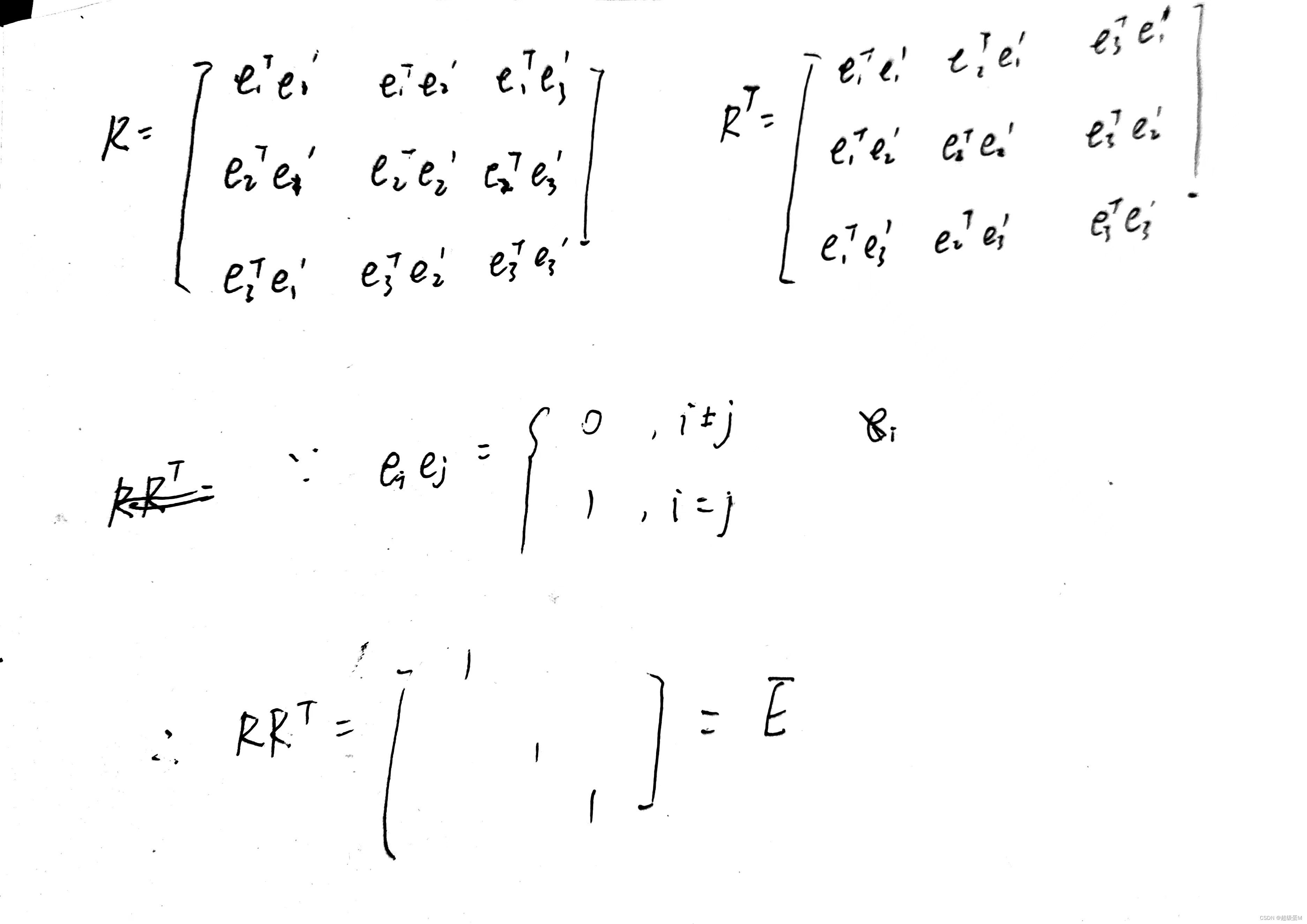
解法二：

2.寻找罗德里格斯公式的推导过程并加以理解。

简单易懂的罗德里格斯公式推导

3.验证四元数旋转某个点后，结果是一个虚四元数（实部为零），所以仍然对应到一个三维空间点，见式（3.33）。

略

4.画表总结旋转矩阵、轴角、欧拉角、四元数的转换关系。

• 旋转矩阵：参数冗余，没有奇异性，自身存在约束（正交矩阵），不直观
• 旋转向量：又称轴角。紧凑，存在奇异性，不存在自身约束，不直观
  旋转矩阵与旋转向量之间转换：罗德里格斯公式
• 欧拉角：直观，紧凑，存在奇异性（万向锁）
• 四元数：既紧凑，又没有奇异性，不直观，运算稍复杂
  四元数与旋转矩阵之间转换见书中公式推导

5.假设有一个大的Eigen矩阵，想把它的左上角3x3的块取出来，然后赋值为 I 。请编程实现。

#include <iostream>

using namespace std;

#include <Eigen/Core>

using namespace Eigen;

#define MATRIX_SIZE 5

int main(){   
     MatrixXf M=Matrix<float,MATRIX_SIZE,MATRIX_SIZE>::Random();
     Matrix3f I;

     cout<<"The large matrix:"<<endl<<M<<endl;

     for(int i=0;i<3;i++){
          for(int j=0;j<3;j++){
               I(i,j)=M(i,j);
          }
     }
     
     cout<<"----------------I-----------------"<<endl<<I<<endl;
}

6.一般线性方程Ax=b有哪几种做法？你能在Eigen中实现吗？

一般线性方程Ax=b的求解可以采用以下几种方法：

1. 直接求逆求解方程。
2. 直接法：包括高斯消元法、LU分解、Cholesky分解等。这些方法通过消元或分解矩阵A，将线性方程组转化为更简单的形式，从而求解出未知变量x。可以使用高斯消元法进行直接求解。
3. D迭代法：包括雅可比迭代法、高斯-赛德尔迭代法、共轭梯度法等。这些方法通过迭代计算，逐步逼近线性方程的解。可以使用共轭梯度法进行迭代求解。

几种求解方法的代码如下

#include <iostream>

using namespace std;

#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/IterativeLinearSolvers>

using namespace Eigen;

int main(){
    Matrix3f A;
    Vector3f x,b;

    A << 2,5,2,
        1,7,9,
        5,4,0;

    b << 3,4,5;

    // 直接求逆
    x=A.inverse()*b;
    cout<<"直接求逆："<<endl<<x<<endl;

    // 直接法QR分解
    x=A.colPivHouseholderQr().solve(b);
    cout<<"QR分解："<<endl<<x<<endl;

    // 直接法LU分解
    x=A.lu().solve(b);
    cout<<"LU分解："<<endl<<x<<endl;

    // 迭代法（共轭梯度）
    int maxIterations = 100;    //最大迭代次数
    float tolerance = 1e-4;     //容差值

    ConjugateGradient<Matrix3f> cg;     //共轭梯度求解器
    cg.setMaxIterations(maxIterations);
    cg.setTolerance(tolerance);
    cg.compute(A);
    x = cg.solve(b);
    cout<<"共轭梯度迭代法："<<endl<<x<<endl;
    // cout << "iterations:      " << cg.iterations() << endl;
    // cout << "estimated error: " << cg.error() << endl;
}