特解的一万种考虑方法

在做微分方程的题目的时候，我遇到了一些刁钻的题目，它要我求解该方程，那么按照解题思路呢，对于二阶线性微分方程，我们会得到两个特征根，它分为三种情况嘛，然后我们可以选择通解的形式，然后再进行后续操作
其实我在学习的时候是搞不懂这些东西的啊，微分方程不能直接求解吗？为什么要背公式？特征根有什么特征？常系数是什么系数？线性是怎么个线性？齐次有多齐？等等一系列问题，为了整理这样的问题呢，我就写了这篇文章。

微分方程

阶

微分方程中最高阶导数的阶数为方程阶数

解

就是y=f（x）是啥样

通解

特解

解的一部分，不包含任意常数的解

前缀系列

可分离变量

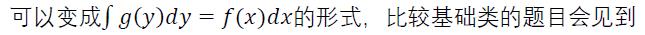
齐次

一阶线性

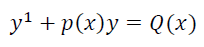
一阶线性的通解

问就是直接背，反正二阶还有，背个简单的好去背难的

二阶线性

齐次

常系数（就是系数变成常数咯）

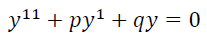
非齐次

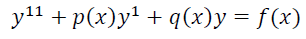
常系数

二阶常系数齐次线性的通解

特征根为实数

相等

不相等

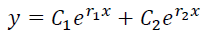
特征根为共轭复数α±iβ

常系数非齐次线性的特解（重点）

本次的重中之重，下边来分析这个名字

1. 常系数指P和Q为常数，不含有未知数x
2. 非齐次指等号右边有f（x）
3. 线性指y``+py`+qy这个样子

那么它的一般形式为

这玩意显然上边已经出现过了，请按目录翻一翻
那么就得按照f（x）的形式来分类，这就是我们经常遇到的问题了，怎么去考虑它的形式

---

2021年0830更新，使用这个套特解形式的方法只能适用于当等式右边的$e^{Ax}$中A为特征值时才能套，如果不是特征值的话，那就不用这样去套，个人认为可以直接把k置零，详见更新的例题

---

举个例吧：

可以解出两个特征根相等，都等于3，刚好和f（x）里的α相等（一般都会相等吧大概），那么上述的k=2，然后P（x）=1，则Q（x）=C，只能次数相等，然后我们已经得到了特解，即：

把这个带入原本的微分方程里去，可以求解出C（C=0.5）

例2：

特征根为1和2，两个特征根为实数且不相等，则Q（x）=C，特征根不重复，则k=1，故有特征根的第一部分：

特征根的第二部分勒，就写成：

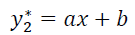
这题里边只问特解所具有的形式，而非具体的答案，因此上述abc都可以换为其他代表常数的字母

更新例题3

$y^{(2)}-4y^{(1)}+3y=2e^{2x}$
解：首先考虑对应齐次方程的特征方程：
${\lambda }^2-4\lambda +3=0$并由此得出齐次方程对应的通解$\overline{y}$
(本版块重点在于特解的形式而不是通解，故略过)
然后设非齐次方程的特解为$y^{\ast }=A{e}^{2x}$，代入原方程得A=-2
由此得出非齐次方程的通解

• 错误套壳：
  由特征方程的重复根数为1，即k=1，考虑$y^{\ast }=Ax{e}^{2x}$
• 结果：
  带入原方程后，$B(A)x{e}^{2x}$无法消除，同时A$\ne 0$，则会让人觉得很懵逼，并且浪费解题时间，正常情况下这项会消除，并且只留下$B(A)e^{2x}$然后顺利解出A的值

这一种看起来就很恶心的类型，但能解决的问题就直接解决比较好，难的是不能解决的问题

例题1（非常的抽象）：

特征根为±ik（或±jk），通解形式已决定，考虑特解形式，最复杂的情况就是

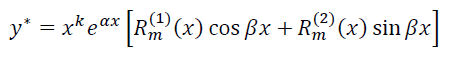
这样的完全体！（我看着压力就大）
跟原式对比一下

完全抄下来的部分有三角函数部分
所以上述cos x直接抄下来，没有包含exp（x），放松放松（压压惊
那么我们可以把公式简化为

Cos x前没有P（x）故R（x）=常数（再把这个式子简化一下吧，我压力好大）

决定k的是复数中ik是不是齐次微分方程的单个特征根，什么是齐次微分方程？看下边

怎么看是不是单个特征根呢？
假设它不是，那么k=0，则

直接代入原微分方程去验证，可以解得B=0，A=-1
假设它是，则k=1，则

带入原微分方程去，则A=0，B=0.5

例题2（好多了）：

特征根为1±2i，为复数，则k=1，三角函数前有exp（x），原封不动搬下去，三角函数也原封不动地搬下去，三角函数前没有x的次方项，因此需要带入两个系数到正弦和余弦，即

带入原微分方程求解A和B，解得A=0，B=0.25，翻到参考答案，结果正确，完美！

总结

从不敢看这个结论到看得清清楚楚，我觉得今天我有很大的进步，给自己点个赞嗷，考研加油