SLAM_轨迹算法精度评价指标（ATE、RPE）

惊鸿一博

已于 2023-02-21 10:31:36 修改

阅读量2.4w

点赞数 27

分类专栏： SLAM 文章标签：算法自动驾驶机器学习

于 2021-03-21 19:31:59 首次发布

原文链接：https://zhuanlan.zhihu.com/p/105428199

版权

SLAM 专栏收录该内容

227 篇文章 ¥29.90 ¥99.00

订阅专栏

超级会员免费看

本文详细介绍了SLAM算法中用于精度评价的两个关键指标——相对位姿误差(RPE)和绝对轨迹误差(ATE)，并讨论了它们的计算方法和意义。RPE用于衡量固定时间间隔内位姿变化的精度，而ATE直接计算估计轨迹与真实轨迹的差异。文章还提到了EVO工具的使用，这是一个用于评估SLAM和里程计性能的实用工具。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 前言

2. 相对位姿误差 (Relative Pose Error, RPE)

3. 绝对轨迹误差 (Absolute Trajectory Error, ATE)

参考：视觉SLAM基础：算法精度评价指标（ATE、RPE）

SLAM中的位姿与轨迹评价指标:APE、RPE、ATE、RTE

1. 前言

当我们需要评估一个SLAM/VO算法的表现时，可以从时耗、复杂度、精度多个角度切入，其中对精度的评价是我们最关注的，这个过程中不可避免会遇到两个精度指标ATE和RPE。这两个evaluation metrics最早是在TUM数据集benchmark中定义的，应用非常广泛。介绍前，先对定义一下公式中的符号表示：
估计位姿：
真实位姿：
下标：代表时间t（或帧）,这里我们假设估计位姿和真实位姿各帧时间已对齐，总帧数相同
：表示相隔时间time interval。

2. 相对位姿误差 (Relative Pose Error, RPE)

（对应evo工具中的“evo_rpe”命令）

相对位姿误差（relative pose error）用于计算相同两个时间戳内的位姿变化量的差，同样，在用时间戳对齐之后，真实位姿和估计位姿均每隔一段相同时间计算位姿的变化量，然后对该变化量做差，以获得相对位姿误差，该标准适合于估计系统的漂移。

相对位姿误差主要描述的是相隔固定时间差两帧位姿差的精度（相比真实位姿），相当于直接测量里程计的误差。

因此第i帧的RPE定义如下：

已知总数n与间隔的情况下，可以得到个RPE，然后我们可以用均方根误差RMSE统计这个误差，得到一个总体值：

其中代表取相对位姿误差中的平移部分translation。当然也有人不用RMSE，直接使用平均值、甚至中位数来描述相对误差情况。需要注意的是，RPE包含了两部分的误差，分别是旋转误差和平移误差，通常使用平移误差进行评价已经足够，但是如果需要，旋转角的误差也可以使用相同的方法进行统计。到这一步，我们基本可以从RMSE值的大小来评价算法的表现，然而实际情况中，我们发现对的选取有多种选择，为了能综合衡量算法表现，我们可以计算遍历所有的RMSE的平均值：

但这样新的问题又出现了，这样的计算复杂度非常高，很耗时间，因此TUM在自己给定的工具中，通过计算固定数量的RPE样本计算一个估计值作为最终结果。

3. 绝对轨迹误差 (Absolute Trajectory Error, ATE)

（对应evo工具中的“evo_ape”命令）

绝对轨迹误差（absolute trajectory error）**直接计算相机位姿的真实值与SLAM系统的估计值之间的差。程序首先根据位姿的时间戳将真实值和估计值进行对齐，然后计算每对位姿之间的差值，并最终以图表的形式输出，该标准非常适合于评估视觉 SLAM 系统的性能。

绝对轨迹误差是估计位姿和真实位姿的直接差值，可以非常直观地反应算法精度和轨迹全局一致性。需要注意的是，估计位姿和groundtruth通常不在同一坐标系中，因此我们需要先将两者对齐：

对于双目SLAM和RGB-D SLAM,尺度统一，因此我们需要通过最小二乘法计算一个从估计位姿到真实位姿的转换矩阵 ；
对于单目相机，具有尺度不确定性，我们需要计算一个从估计位姿到真实位姿的相似转换矩阵 。

因此第i帧的ATE定义如下：

与RPE相似，建议使用RMSE统计ATE

当然，使用平均值、中位数等来反应ATE亦可，现在很多evaluation工具会将RMSE、Mean、Median都给出。综上，我们需要注意的是，RPE误差包含了translation和rotation两部分的误差，而ATE只包含translation的误差（从二者的全称中也可以看出），二者具有强烈的相关性，却也不尽相同。我们仍需结合实际，选择合适的指标进行算法评价。

4. 工具：EVO

这里推荐一个方便全能的evaluation工具。这里贴出github链接：

EVO:Python package for the evaluation of odometry and SLAM

4.1 安装

系统：ubuntu，首先确保系统安装了Python，然后根据需要可以选择性安装PyQt5 / PyQt4 和 ROS，当然，不装也不会影响基本功能。

1. 直接从pip安装。

pip install evo --upgrade --no-binary evo

2. 源代码安装

git clone git@github.com:MichaelGrupp/evo.git
cd evo
pip install --editable . --upgrade --no-binary evo

3. 输入下面这个命令，如果成功会有响应。

evo_ape -h

4.2 usage

可以先用evo仓库中自带的数据尝试

1). 轨迹可视化

cd test/data
evo_traj kitti KITTI_00_ORB.txt KITTI_00_SPTAM.txt --ref=KITTI_00_gt.txt -p --plot_mode=xz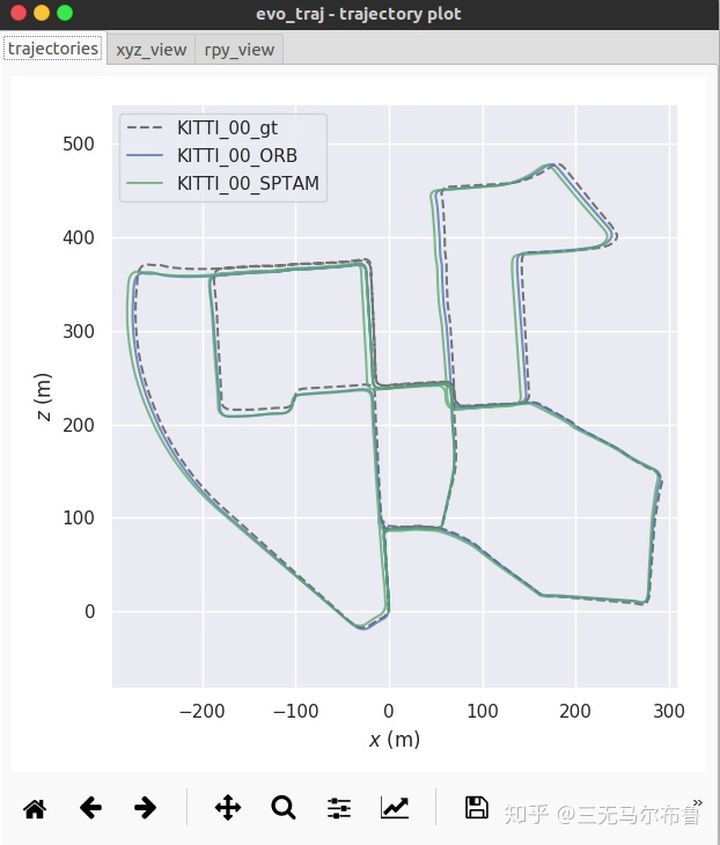

2). APE （ATE）

evo_ape kitti KITTI_00_gt.txt KITTI_00_ORB.txt -va --plot --plot_mode xz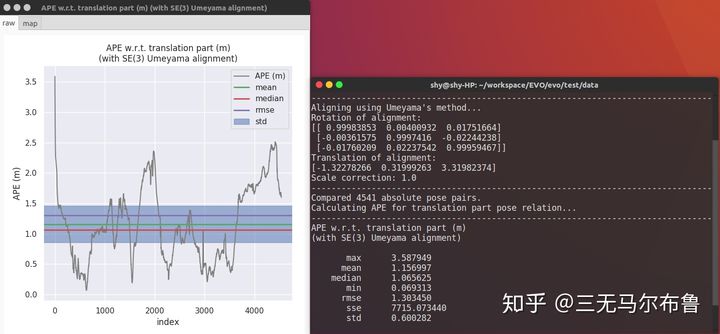

3). RPE

evo_rpe tum fr2_desk_groundtrutr2_desk_ORB.txt -va --plot --plot_mode xyz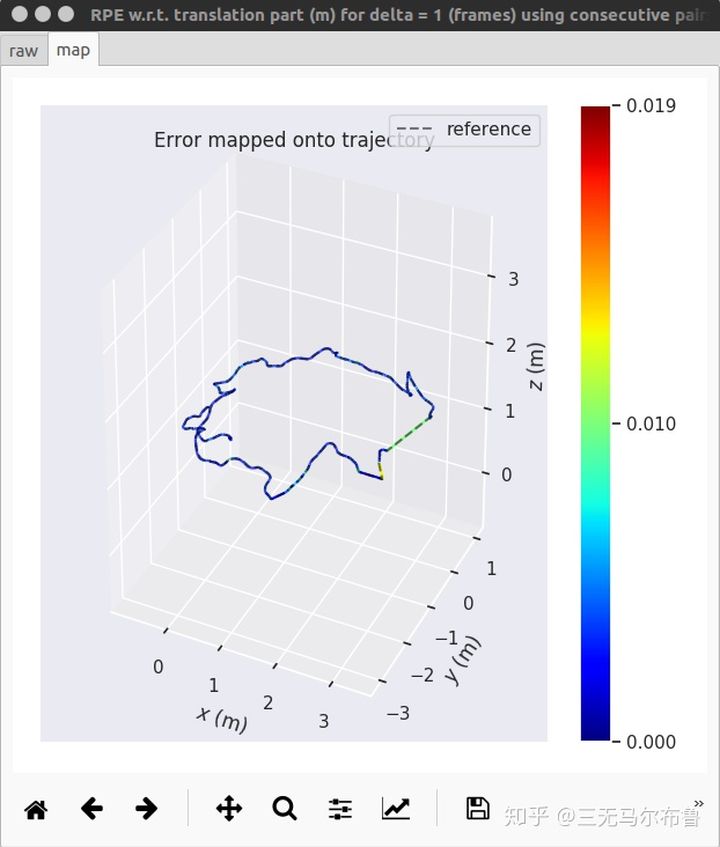

命令参数较多，每个命令都有比较详细的帮助，多用 --help，如：evo_ape kitti --help

这里列举了一些常见选项的含义：

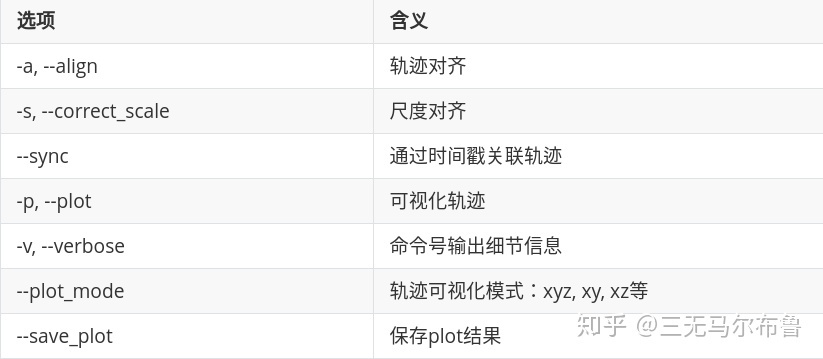
4.3 metrics解析

上文提到pose error包含平移和旋转两部分误差，在evo设置输出误差项对应的option为-r/–pose_relation，并有如下模式：

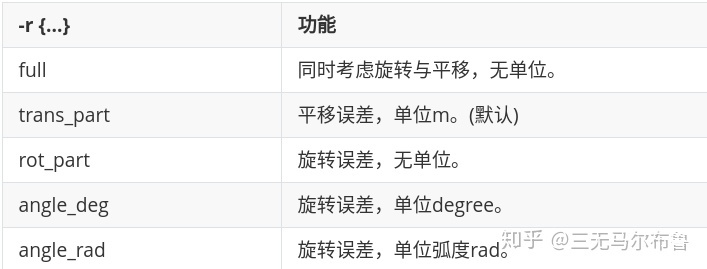
其中trans_part很容易理解，但是无单位的full和rot_part的误差指标比较特殊，使用了矩阵的二范数：

其中表示groundtruth和estimate位姿之间的变换矩阵， E 为单位阵，这里用了矩阵的范数表示某种抽象的空间距离，从而用来度量误差，因此没有单位（仅供参考，这一块不确定，还行批评指正）。

同理rot_part的误差：

相比较而言，用平移误差单位为m，旋转误差单位可以是度或弧度，更容易理解。从旋转矩阵 R 到旋转角的转换使用了罗德里格斯公式（旋转向量的二范数为旋转角的大小）。

反推：

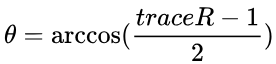
这里参考了《SLAM十四讲》中的内容。

#附EVO metric的相关代码
if self.pose_relation == PoseRelation.translation_part:
    # E is an array of position vectors only in this case
    self.error = [np.linalg.norm(E_i) for E_i in self.E]
elif self.pose_relation == PoseRelation.rotation_part:
    self.error = np.array([
        np.linalg.norm(lie.so3_from_se3(E_i) - np.eye(3))
        for E_i in self.E])
elif self.pose_relation == PoseRelation.full_transformation:
    self.error = np.array(
        [np.linalg.norm(E_i - np.eye(4)) for E_i in self.E])
elif self.pose_relation == PoseRelation.rotation_angle_rad:
    self.error = np.array(
        [abs(lie.so3_log(E_i[:3, :3])) for E_i in self.E])
elif self.pose_relation == PoseRelation.rotation_angle_deg:
    self.error = np.array([
        abs(lie.so3_log(E_i[:3, :3])) * 180 / np.pi for E_i in self.E
    ])
else:
    raise MetricsException("unsupported pose_relation")