首先, 处于3D空间中的每个对象, 实际上都有自己的局部坐标系, 而旋转某个对象时, 其局部坐标系也会跟着旋转。
所以, 如果可以描述某个对象的局部坐标系(每根轴的朝向), 就可以表示该对象的旋转程度。
Quaternion LookRotation(Vector3 forward, Vector3 upwards);
这个函数就是根据对局部坐标轴的描述, 构造对应的代表旋转程度的四元数。
forward:向前向量, 即z轴的朝向。但是仅仅有z轴的朝向是不够的, 因为对象还可能绕着z轴旋转, 所以需要upwards来约束。
upwards:向上向量, 注意, 此向量不需要是精确的y轴的朝向(即不需要与forward垂直), 但是, 此向量应该处于z轴、y轴平面上。
题外话, 那么是如何得到正确的up向量(y轴的朝向)的呢?
可以先以forward、upwards求出right向量(x轴的朝向), 再以forward、right求出up向量(y轴的朝向), 即可。
下面是一个测试例子,
public Transform cube; // 位于(0, 3, 0)的一个cube的transform
public Vector3 target; // cube的朝向目标, 初始值为(0, 3, 0)
void Update()
{
cube.rotation = Quaternion.LookRotation(target - cube.position, Vector3.up); // 注意, 此处Vector3.up并不一定与target - cube.position垂直
Debug.DrawLine(Vector3.zero, cube.forward, Color.blue); // 绘制每根轴
Debug.DrawLine(Vector3.zero, cube.right, Color.red);
Debug.DrawLine(Vector3.zero, cube.up, Color.green);
}
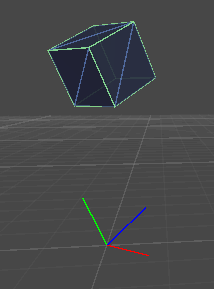
运行例子, 调整target的值, 可见Scene视图中, cube以及绘制出来的局部坐标轴也相应地发生了变化。






















 4173
4173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








