文献摘录_0510

西安市近50年来气候变化多时间尺度分析①②（邓自旺，1997）

摘 要

        利用Morlet小波变换法分析了西安市近50年月平均气温距平和月降水量距平变化的多层次时间尺度结构，发现西安市气候变化除1年的自然周期变化和20～40年尺度范围的周期变化信号在全时间域中都强外，其它时间尺度的周期变化在时间域中分布很不均匀，具有很强的局部化特征。

        西安市月平均气温距平变化主要表现为随机振荡，无特征尺度，而月降水量距平变化则有显著的4～5月的时间尺度。

西安市气候变化受地理条件的影响较大，与ENSO的关系不象我国沿海地区那么紧密。对于大时间尺度来说，西安市气候呈暖干和冷湿结构排列，而对于小时间尺度而言则呈现为复杂的冷暖和干湿结构。

00 前言

地球上几乎所有的天气和气候现象均与多时间尺度相联系，特别是气候变化，包含多种时间尺度，从月季尺度的气候异常到万年尺度的冰期间冰期的转换。短期气候变化与人类的生存息息相关，当前主要研究的是月季尺度、年际尺度和几十年尺度的长期变化。严中伟等〔1〕的研究表明，气候的变化不但具有全球性，而且具有局地特征。王绍武〔2〕用哈尔滨、北京、上海及广州4个站的平均气温作为中国的气温序列，研究其变化，但这些站均处在我国沿海地带，不能代表地处内陆的西安市的气候变化。

另外，传统的分析方法一般是傅里叶分析和滤波分析，以找出气候资料中所包含的周期并与诸如太阳黑子周期等已知的周期相比较为目的。

但事实上，气候变化并不存在真正意义上的周期性，而是时而以这种周期变化，时而又以另一周期变化，并且同一时段中又包含各种时间尺度的周期变化。

即气候变化在时域中存在多层次时间尺度结构和局部化特征，但传统的傅里叶分析却不能分析出这一特征。

近年来发展起来的小波分析方法，是泛函分析、Fourier分析、样条分析、调和分析和数值分析的最完美的结晶。

由于其在时频域中都具有良好的局部化特征，所以，是分析气候资料中所包含的周期性及其不均性的有力工具。

1 计算方法

1.1 Morlet小波及小波变换方法

关于小波分析方面的文献有很多〔3，4〕，这里只将本文中用到的Morlet小波及有关的计算公式作一说明。

在气候资料序列中包含有多种时间尺度的周期变化，这些尺度并不成2的整指数幂形式变化，而是连续变化的，故不宜用离散或正交小波变换来进行分析。虽然连续小波变换实际上也是以离散的形式来完成的，但尺度的间隔可以取到资料本身分辨率许可的大小。与非2的整指数幂尺度相对应的频率成分能够比较精确地被探测出来。当尺度的间隔取得很小时，尺度的变化可看成是连续的。

复数形式的小波，因其实部和虚部的位相差为π／2，用复小波变换系数的模来作为判别气候资料中包含的各尺度周期性的大小及这些周期在时域中分布的判据，能够消除用实型小波变换系数作为判据而产生的虚假振荡，使分析结果更准确。

另外，复小波变换可同时给出资料序列变化振幅和位相两方面的信息，而实小波变换则只能给出振幅和正负。所以，本文中采用连续Morlet小波作为基函数进行小波变换。它能够很好地对资料序列连续进行时频局部化分析。Morlet小波及其傅氏变换波形如图1所示。

图1 Morlet小波及其傅里叶变换示意图

Fig．1 TheMorletwaveletsandtheirFouriertransforms．

Morlet小波的形式为

本文取C＝5．4，其子小波为

其傅氏变换为

设f（x）为信号，其小波变换为

其中，符号〈·，·〉表示内积运算符，“＊”表示共轭运算符；

a为伸缩尺度，b为平移参数。

这样就把原始信号分解到时间－尺度平面上，可以清楚地研究其在时－频域中的局部特征。

对于许多小波函数来说，其伸缩尺度a与傅里叶分析中的周期T并没有一一对应的关系。

如某些小波函数是高度不规则的，不存在显著的周期变化成分，这时如要找出尺度a与周期T之间的对应关系将毫无意义。

但本文中所用的Morlet小波函数是一个周期函数并经一个Gaussian函数平滑而得到的，所以，它的伸缩尺度a与傅里叶分析中的周期T有一一对应关系〔5〕：

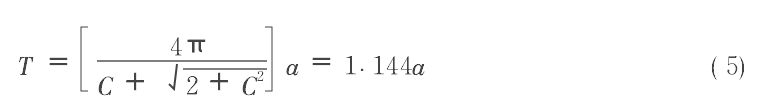
这使得对计算结果的解释更简单明了。由于子波分析是傅里叶分析的发展，傅里叶变换可以认为是嵌套在子波变换里面的。在近似情况下，通过对所有时刻子波变换系数求和的方法求得Fourier谱。但在子波分析中度量信号的整体属性时更常用的是子波能量（实际上也是信号能量）在各尺度的分布。其算法如下

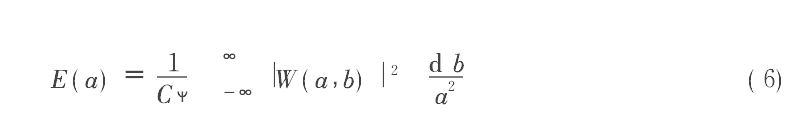
1.2 资料预处理及计算方法

本文所用的资料为1939年1月～1988年12月西安市月平均气温和月总降水量资料（图2）。在进行小波变换以前，通过求距平的方法将资料中一年的自然周期滤去，因此，实际上用来变换的资料序列为距平序列。虽然Morlet小波具有很小的支集，但在资料两端点附近Morlet变换也象其它小波变换一样在资料的开始点和结尾点附近有边界效应影响。为了减小这种影响，有必要在序列的两端支垫一些资料。我们在序列两端分别增加了600个资料，这样序列总长为1800月。用这一资料序列进行小波变换，变换结束后将两端1200个小波变换系数去掉，保留原有序列时段600个小波系数。增加端点资料的方法如下：设原资料序列为f（1），f（2），…，f（600）。其中f（1）对应于1939年1月资料，f（600）对应于1988年12月资料，其余依次类推，然后周期性地向两边延伸。向前延伸600点：

向后延伸600点：

这样资料序列就变为f（－599），f（－598），…，f（1200）。小波系数用（4）式数值积分方法求得。在小波分析中，伸缩尺度越大，在时域中分辨率越低，在频域中分辨率越高，否则相反。故对小尺度变化，a的间隔要取小，对大尺度变化，

a的间隔要取大，这样既不会影响计算结果，又可以节省机时。本文中伸缩尺度a的取值如下

对应的周期为3个月～50年。

2 结果分析

因本文所用资料为月平均距平资料序列，长度为50年，所以只限于讨论月季尺度、年际变化和年代际这3种时间尺度的变化。

2．1 西安市近50年来气温变化多层次时间尺度分析

图2a为近50年（1939年1月～1988年12月）月平均气温距平序列的低通滤波曲线。

图3a～c为该序列Morlet小波变换系数的模、位相和实部在时－频域中的分布图。

横坐标为时间t，纵坐标为周期T（3个月～50年）。

因伸缩尺度和周期一一对应，所以图中没有标出a。

图3a中曲线为小波系数模值等值线，间隔为1.5。

图3b为小波系数位相等值线图，变化范围为［－π，π］，间隔为1.57，显然－π等值线与π等值线相重合，如图中粗黑线所示。

图3c为子波变换系数实部的等值线图。

图中虚线为小于零的等值线，实线则为大于或等于零的等值线。

间隔为2．0。

各图中的L，H分别对应于极小值和极大值中心。

图2 西安市月平均气温距平（a）和月降水量距平序列低通滤波曲线（b）

Fig．2 Thelowpassfilteringcurvesofanomalousseriesofmonthlymeantemperature（a）andmonthlyprecipitation（b）inXi′an．

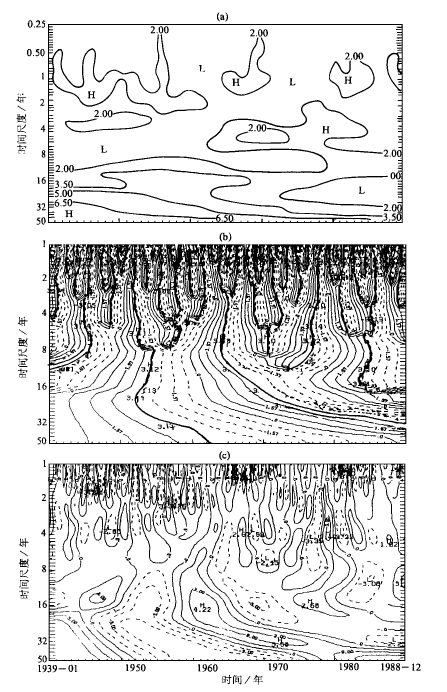
图3 西安市月平均气温距平Morlet小波变换系数的模（a）、位相（b）和实部（c）

Fig．3 Themodulus（a），phase（b），andrealpart（c）oftheMorletwavelettransformcoefficientsofmonthlymeantemperatureabnormalsinXi′an．

显然，从图2中看不出气温变化的周期性，更看不出周期变化在时间域中的分布情况，而从图3中则可以清楚地看到，特别是图3a可以把各种时间尺度周期变化在时间域中的分布情况展示出来。

小波变换系数模值越大，表明其所对应的时段和尺度的周期性越明显，但较小尺度周期变化在图3b，c中不能清楚地被分辨出来。

这不是由于Morlet小波变换本身存在的问题，而是由于我们不可能在同一张图中把所有尺度的变化都表现出来。只需将图中局部进行放大（如图4），就可以达到目的。

2.1.1 月季尺度的周期变化

从图3a顶部对应于3个月～1年的部分可以看到，西安市气温对应于6个月以下尺度变化的子波变换系数均很小，说明该尺度范围的周期性在整个时段都非常弱。6个月～1年尺度的周期变化在时域中分布很不均匀，即具有局部化特征。如1944～1946年，1953～1955年等有较明显的这一周期范围的变化。但总的来说，月季尺度的周期性较差。

2.1.2 年际尺度的周期变化

这一尺度范围对应于图3a中1～10年的部分。..1～2年的周期变化大约在4个时段有较强的信号。如1943～1948年16个月～2年的周期变化，1949～1961年2年左右的周期信号，1964～1969年和1979～1988年的1年～16个月左右的周期信号；而在其余时段周期性则较差。2～10年尺度的周期在1960～1984年以后也都有较强的信号，其中最强的时段为1974～1980年的3～5年左右的周期变化。2．1．3 年代际尺度的周期变化这一尺度范围对应于图3a中10～50年尺度的部分。对于大于50年尺度的变化，因资料长度所限本文对此不进行讨论。由图3a可见，在1970年以前的32年中具有明显的13～50年尺度的周期信号，其中最明显的信号为1963年以前的20～40年尺度左右的周期信号，而40～50年的周期性变化在时域中没有局部化特性，而是全域的。值得一提的是，小波变换系数模的大小不代表各种周期变化成分能量的大小，这一点与傅里叶分析是完全不同的。用小波分析可以把傅里叶分析不能分析出来的很弱的信号分析出来。如本文中的大尺度周期信号，其模值虽然很大，但实际上这些信号对整个原始信号的方差贡献是很小的。位相图是用来探测信号的奇异点或突变点的存在和位置。由图3b可见，对各尺度的变化，其位相从左到右从－π变化到π，－π和π相邻，它们之间非常清楚的分界线是一常位相线。等位相线应当是连续光滑曲线，由于绘图软件的缺陷而使绘出来的线条是阶梯形的，这不是Morlet小波变换本身的问题，且不影响对结果的分析。当信号有奇异点或突变点时，常位相线辐合到一小的区域上。如与8年尺度相对应的1962～1968年区域的等位相线1年尺度的周期辐合到1965年附近的很小的区域上。而这一锥形区域就是所谓的“影响锥”。某一点的“影响锥”是指与该点相对应的所有尺度子小波的支集所组成的锥形区域。它表明了该点在子波系数计算中的影响范围，由此，我们不难看出由于资料长度所限对各子波系数的影响程度。显然，对于小尺度而言，只有两端很少一部分结果受影响，中间部分则不受任何影响；而对于大尺度而言，受影响的区域则相应增大。

但由于我们采用对称外延方法对其进行处理和小波本身的支集很小，使边界效应的影响大大减小。小波系数的实部包含着给定时间和尺度信号相对于其它时间和尺度信号的强度和位相两方面的信息。图3c是图3a，b的综合情况。

从该图底部32～50年尺度的部分可以看到两个明显的正值区和一个负值区组成的准一次振荡。1970年以前的16～32年尺度的周期振荡也可以清楚地看到这一情况。另外，Morlet小波的实部本身也是一个对称小波函数，它可以看成是一个平滑函数的二阶导数，所以，Morlet小波变换系数的实部与墨西哥帽小波变换系数一样，也可以用来判别气候资料序列中所包含的不同时间尺度下的冷暖和干湿结构。

例如，以32年为尺度来看，西安市近50年来气温变化可分为两个冷段和两个暖段，1948年以前偏暖，1948～1963年偏冷，1964～1979年偏暖，1980年以后又转为偏冷。

以50年为尺度，则仅可以分为两个暖段和一个冷段。对图3c树状结构的任意部分加以放大，则可以看到该部分的详细结构。

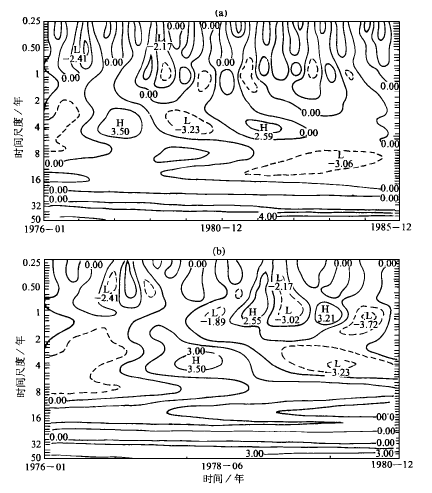
图4 图3c中1976～1985年（a）和1976～1980年（b）局部放大图Fig．4 A“zoomin”picturefromFig．3cforthetimeintervalofyears1976～1985（a）and1976～1980（b）．

 图4是图3c的局部放大图。从该图可以很清楚地看到1979～1984年有明显的1年尺度的周期变化，1976～1982年有明显的2～4年尺度的周期变化信号。用同样的方法可以了解其它时段的小尺度变化情况。

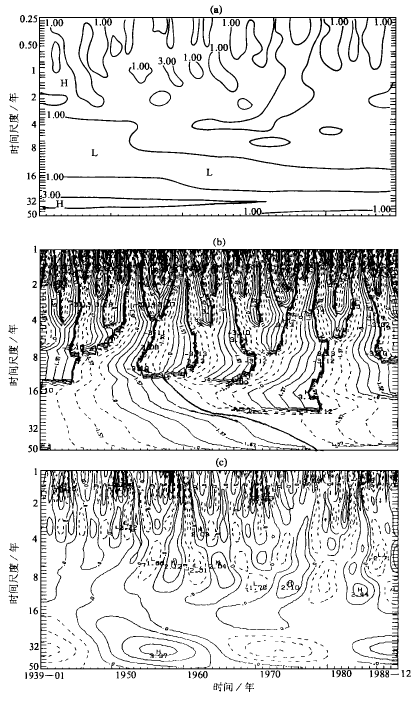
图5 西安市月降水量距平Morlet小波变换系数的模（a）、位相（b）和实部（c）

Fig．5 ThesameasFig．3，butformonthlyprecipitationabnormals．

2．2 西安市近50年来降水变化多层次时间尺度分析

与图3相似，

图5a，b，c分别为西安市降水序列Morlet小波变换系数的模、位相和实部在时－频域中的分布图。

（1） 由图5a可见，西安市降水具有明显的20～40年左右尺度的周期变化。

这一尺度范围的周期变化在整个时域中都存在，特别是在1970年以前大约25～35年尺度的周期变化最为显著。

从该图中可以看到自1939年的4～16年至1988年的12～25年左右有一个清楚的低值带，说明该区域的信号很弱。

8～16年尺度的周期变化在整个50年内都非常弱；

2～8年尺度的周期变化在1950～1960年之间和1975年以后信号较强，但在时－频域内也具有较强的局部化特征。

2年以下尺度的周期变化只有在1948～1950年和1956～1960年较明显，在其余时段均很弱。

（2） 用图5b可以判别降水序列中所包含的突变点的存在性和具体位置。

如8年尺度到1年尺度有5个明显的锥形区域，从8年尺度较大区域辐合到1年尺度较小区域内。

这些辐合点分别为1951，1959，1964，1976和1984年。说明在这些年中西安市降水有异常。

图6 图5中1976～1985年（a）和1976～1980年（b）部分的局部放大图Fig．6 A“zoomin”picturefromFig．5forthetimeintervalofyears1976～1985（a）and1976～1980（b）．

 （3） 从图5c可以看到，西安市降水变化具有明显的20～40年尺度的周期变化。

在该图对应的20～40年部分有两个降水偏少时段和两个偏多时段。

从32年为尺度来看（图7a），则1948年以前降水偏少，1948～1963年偏多，1964～1979年偏少，1980年以后又偏多。

这与气温恰恰反位相。

其中降水最多的时段为1950～1960年。

以8年尺度看，在1950年以后又由5个明显的降水偏多时段和5个降水偏少时段组成准8年的周期振荡；而8～16年尺度范围内的变化则显得比较微弱。这与图5a的分析结果一致。另外，通过对图5c较小尺度部分的放大还可看出西安市降水序列变化更为详细的结构。

（4） 图6是对图5c的局部放大。

图5a为1976年1月～1985年12月的部分。

由此可见，在6个月～1年尺度范围内，1980年1月～1984年12月间有5个较明显的降水偏多和偏少区域组成准1年的周期振荡。

从图6b可以看到2～4年尺度范围内，在1976～1980年有一较为明显的3.5年的周期变化。从该图顶部也可以看到微弱的3～6个月的周期振荡。

图7 时间尺度为32年（a）、16年（b）和8年（c）的气温（实线）和降水（虚线）的变化趋势

Fig．7 Thechangetendenciesoftemperature（solidline）andprecipitation（dashedline）on32（a），16（b）and8（c）yearstimescales．

2.3 初步讨论

比较图3和图5可以看到，气温和降水变化的周期性在时域中的分布有一定的相似性，但并不完全一致。

20～40年尺度的周期变化信号二者都较强，40～50年尺度气温显然比降水变化周期性强；

8～16年尺度范围气温变化还具有一定的周期性，但降水变化在这一尺度范围周期性却很差。

另外，从大尺度来看，气温变化和降水变化位相大约相差180°，即呈干暖、冷湿结构排列。

图7a，b，c分别为32，16和8年尺度时气温和降水子波系数实部的变化曲线。

从中可以清楚地看到时间尺度为32年和16年时完全如此，这反映了气候变化的长期规律。

对于小尺度，则呈现较为复杂的冷暖、干湿结构。

如以8年尺度为例，则可以看出1969年以前降水量变化的位相超前于气温，而以后则相反，但位相差都不超过90°。

图8 气温变化功率谱（a）、子波能谱（b）和降水变化功率谱（c）、子波能谱（d）Fig．8 Thepowerspectrumandwaveletenergyspectrumoftemperature（a，c）andprecipitation（b，d），respectively．

为了从总体上了解西安市近50年来的气候变化情况，我们对气温和降水资料进行了功率谱分析（图8a，b），并用公式（9）进行了能量尺度分解（图8c，d）。

从功率谱图上可以看到，无论是气温还是降水量都不存在显著的周期。

由图8c可以看到，西安市气温变化能量随尺度的增加急剧下降，虽然某些时段表现为周期变化，但它主要表现为随机振荡。

由图8d则可以看到，西安市降水变化能量主要集中在6个月以下尺度，对应于4～5月有一个峰值。

由此看出，西安市降水变化较气温变化有规律，其特征尺度为4～5个月。

一般认为，引起短期气候变化的因子有外界强迫和气候系统内部各子系统之间及气候不同尺度变化之间的非线性相互作用。

外界强迫包括太阳活动（如太阳黑子的11年基本周期，22年的磁周期，5～6年的半黑子周期，2年短周期振动和35年左右的布吕克纳周期等等）、火山活动、海温异常等等。

气候的月季尺度变化主要是由于大气环流异常、海温异常遥相关等引起的。

年际尺度的变化主要是由于ENSO和QBO等引起的。

而年代际尺度变化则主要由太阳活动、火山活动、CO2等温室气体含量的增加等引起的。

但是，从上面分析可见，西安市气温和降水并不完全按外界强迫的变化而变化，除在整个时域中有较强的20～40年尺度的周期变化外，其它尺度周期信号的强弱在时－频域中的分布具有很强的局部特征。

这可能是因为气候系统本身内在的非线性作用而引起的。

另外，西安市气温和降水变化2～7年尺度的周期信号并不强，说明西安市气候变化与ENSO关系并不很大，这可能是因为西安市所处的地理位置所决定的。

因为西安市地处内陆，西有青藏高原，南有秦岭山脉，这种特殊的地理条件使西安气候变化与沿海地带不同，它受海洋的影响大为减少。

3 小  结

由前面分析可以得出西安市近50年来气候变化具有以下特征：

（1） 西安市气候变化具有多层次的时间尺度结构。它是由月季尺度、1～2年尺度、2～4年尺度、4～8年尺度、8～16年尺度和16年以上尺度的周期变化构成的嵌套多层次结构。但这些周期变化在时域上的分布具有明显的局部化特征。气温变化具有较大的随机性，而降水变化则具有4～5个月的特征时间尺度。

（2） 西安市气候变化具有局地特征，并不完全与我国平均情况一致。它与ENSO的关系并不密切。

（3） 西安市气候变化在大尺度下表现为暖干、冷湿结构，而小尺度变化则表现出更为复杂的冷暖、干湿结构。以32年的时间尺度来看，近50年的气候变化可划分为4个阶段，1948年以前为暖干气候，1949～1963年为冷湿气候，1964～1980年为暖干气候，而1980年以后为弱的冷湿气候；以16年时间尺度来看，则可划分为6个阶段，但为暖干和冷湿结构。

（4） 气温与降水变化的小尺度周期性较差，呈杂乱无章的随机振荡，而大时间尺度变化较为规则，为准周期振荡。但从能量变化尺度分布来看，主要表现为月际尺度的变化，降水变化具有4～5个月的特征时间尺度，而气温变化则表现为更大的随机性。

（5） Morlet小波变换是进行时－频分析的有力工具。

参考文献

1 严中伟，季劲钧，叶笃正．60年代北半球夏季气候跃变，（Ⅰ）降水和温度变化．中国科学（B辑），1990，20：97～103

2 王绍武．近百年气候变化与变率的诊断研究．气象学报，1994，52

（3）：261～2733 崔锦泰．小波分析导论．西安：西安交通大学出版社，1995．66～99

4 龙瑞麟．高维小波分析．北京：世界图书出版公司，1995．208～3595

MeyersSD，BGKelly，JJOBrien．An introduction to waveletanalysis in ocean ography and meteorology：with application to the dispersion of Yannaiwaves．MonWeaRev，1993，121：2858～2866