【无人机】非对称多旋翼无人机线性控制的建模、仿真与实现（Matlab代码实现）

最新推荐文章于 2025-05-28 16:37:41 发布

荔枝科研社

最新推荐文章于 2025-05-28 16:37:41 发布

阅读量768

点赞数 20

文章标签：无人机 matlab 数学建模

本文链接：https://blog.csdn.net/weixin_46039719/article/details/148184631

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

非对称多旋翼无人机线性控制的建模、仿真与实现研究

一、非对称多旋翼无人机的结构特点与动力学建模

二、运动学建模与姿态表示

三、线性控制策略

四、仿真工具与实现案例

五、硬件选型与部署

六、实验验证方法

七、挑战与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章下载

💥1 概述

摘要：

无人驾驶飞行器(uavs)是不直接由机载人员控制的空中系统。UA - V平台有很多种类型，主要由其机械结构的特点来定义。其中一类无人机是具有多个旋翼执行器的多旋翼无人机。这些类型的无人机由于其执行垂直/短距起降(VSTOL)，静止和低速飞行的能力，以及与单旋翼结构相比相对简单的机械设计，具有广泛的应用范围。

处理这些类型的无人机的主要挑战是它们在飞行中固有的不稳定性，除了复杂控制系统的干预。因此，为了了解能够产生保证性能的控制系统，该项目首先寻求通过数学建模来研究无人机的物理特性和响应，然后再进行设计、开发、实施和比较嵌入式微处理器上2种先进线性控制方案的性能，其中这种水平的洞察力是必要的。这些控制方案是线性二次高斯(LQG)和线性二次模型预测控制(LQ-MPC)。

本文研究基本框架围绕垂直/短距起降（VSTOL）模型飞机的控制软件的设计和开发展开。从该主题出发，推导出了非对称垂直起降多旋翼平台非线性动力学建模与仿真以及比例积分导数、线性二次高斯和模型预测控制算法等多种控制方案的开发。然后，这些控制方案将通过嵌入式微处理器单元在建模的多旋翼平台上实现。

这些目标分为多个目标和里程碑，每个目标和里程碑都必须实现，才能实现所概述的目标的全部范围。这些目标大致可分为两类：

基本目标

开发一个表示多旋翼飞机动力学的数学模型。
开发工艺品行为的动态模拟。
开发反馈控制定律：线性二次高斯（LQG）。
使用数学模型在模拟中研究反馈控制定律，以实现行为目标。
开发飞行控制软件以与传感器接口并实施控制法则。
在嵌入式微处理器单元上实现飞行控制软件。
将控制器安装到多旋翼平台上。
讨论仿真和硬件实现之间的性能比较结果。

高级目标

研究模型预测控制（MPC）方案在仿真中的应用。
将MPC方案合并并实施到飞行控制软件中。
讨论 LQG 和 MPC 实现之间的差异

非对称多旋翼无人机线性控制的建模、仿真与实现研究

一、非对称多旋翼无人机的结构特点与动力学建模

结构特点
非对称多旋翼无人机通过采用不同尺寸、倾角、转速的旋翼布局（如可变形、多层或螺旋桨异向设计），显著提升了负载能力和飞行时间，但也导致重心偏移、推力和力矩分布不对称等问题。这种不对称性使得其动力学方程比传统对称结构复杂，需在建模时考虑以下因素：
- 重心偏移：旋翼分布不均导致重心偏离几何中心，需重新定义机体坐标系原点。
- 非对称推力与力矩：各旋翼的升力与扭矩差异需通过精确的力臂计算纳入动力学方程。
动力学建模方法
- 牛顿-欧拉方程：基于力与力矩平衡，适用于姿态角变化较小的情况，计算直观但复杂度随自由度增加而显著提升。
- 拉格朗日方程：通过能量分析（动能与势能）推导方程，更适合复杂多旋翼系统，但需处理非线性项和高阶导数。
- 对比：牛顿-欧拉法物理意义明确但计算繁琐；拉格朗日法系统性强，但需线性化简化；Udwin-Kalaba方程适用于高维系统。

二、运动学建模与姿态表示

姿态角（欧拉角）
- 定义：通过俯仰角（Pitch）、滚转角（Roll）、偏航角（Yaw）描述机体相对于惯性坐标系的姿态，直观但存在万向锁问题（当俯仰角接近±90°时无法区分Roll与Yaw）。
- 应用：适用于小角度控制或简化仿真场景。
四元数
- 定义：由实数部分和三个虚数部分组成（如q=w+xi+yj+zkq=w+xi+yj+zk），无奇异性，可全局描述旋转。
- 优势：计算效率高，避免三角函数运算，适合大角度变化与实时控制。
- 转换方法：通过旋转矩阵或微分方程实现四元数与欧拉角之间的转换。

三、线性控制策略

PID控制
- 原理：通过比例（P）、积分（I）、微分（D）环节调节误差，结构简单且易于实现，但对模型精度依赖低，适用于基础姿态控制。
- 局限性：难以处理多变量耦合和非线性问题，性能受限于线性假设。
LQR/LQG控制
- LQR（线性二次调节器） ：通过最小化状态误差和控制输入的二次代价函数设计最优控制器，需系统线性化。
- LQG（线性二次高斯） ：结合LQR与卡尔曼滤波，处理系统噪声和测量噪声，鲁棒性强但计算量大。
模型预测控制（MPC）
- 原理：基于滚动时域优化，预测未来状态并求解最优控制序列，可显式处理约束条件（如执行器饱和）。
- 适用性：适合非对称系统的动态调整，但实时性要求高，需高性能处理器。

四、仿真工具与实现案例

MATLAB/Simulink
- 建模流程：
  1. 建立动力学模型（牛顿-欧拉或拉格朗日方程）。
  2. 设计控制回路（如串级PID或LQR），验证姿态与轨迹跟踪性能。
  3. 通过Stateflow实现状态机逻辑（如飞行模式切换）。
- 案例：在Simulink中搭建非对称模型，对比PID与LQG的跟踪误差，优化参数后生成嵌入式代码。
ROS/Gazebo
- 优势：支持硬件在环（HITL）与多机协同仿真，逼真模拟环境扰动（如风力）。
- 实现：将动力学模型集成至Gazebo插件，通过ROS节点实现控制算法与传感器数据交互。

五、硬件选型与部署

核心组件
- 处理器：ARM Cortex-M系列（实时性强）或Intel Edison（支持复杂算法）。
- 传感器：
  - IMU（陀螺仪、加速度计）需高精度滤波（如卡尔曼滤波）。
  - GPS模块支持差分定位以提升位置精度。
- 动力系统：BLDC电机搭配电子调速器（ESC），需标定推力-转速曲线以匹配非对称需求。
部署优化
- 实时性保障：采用RTOS（如FreeRTOS）或优先级中断机制。
- 通信可靠性：使用冗余链路（如2.4GHz与900MHz双频）和协议校验。

六、实验验证方法

仿真验证
- 开环测试：验证动力学模型与真实物理行为的一致性。
- 闭环测试：对比不同控制器在轨迹跟踪、抗扰动（如突风）下的性能。
实物实验
- 硬件在环（HIL） ：通过PX4或Pixhawk飞控连接仿真模型，测试算法实时性。
- 外场飞行：记录实际飞行数据（如姿态角、位置偏移），与仿真结果对比以验证模型精度。

七、挑战与展望

当前挑战
- 非线性动力学的高效线性化方法仍需改进。
- 计算资源限制下复杂算法（如MPC）的实时部署。
未来方向
- 自适应控制：结合在线参数辨识，应对负载变化。
- 智能优化：利用强化学习或神经网络优化控制器参数。

📚2 运行结果

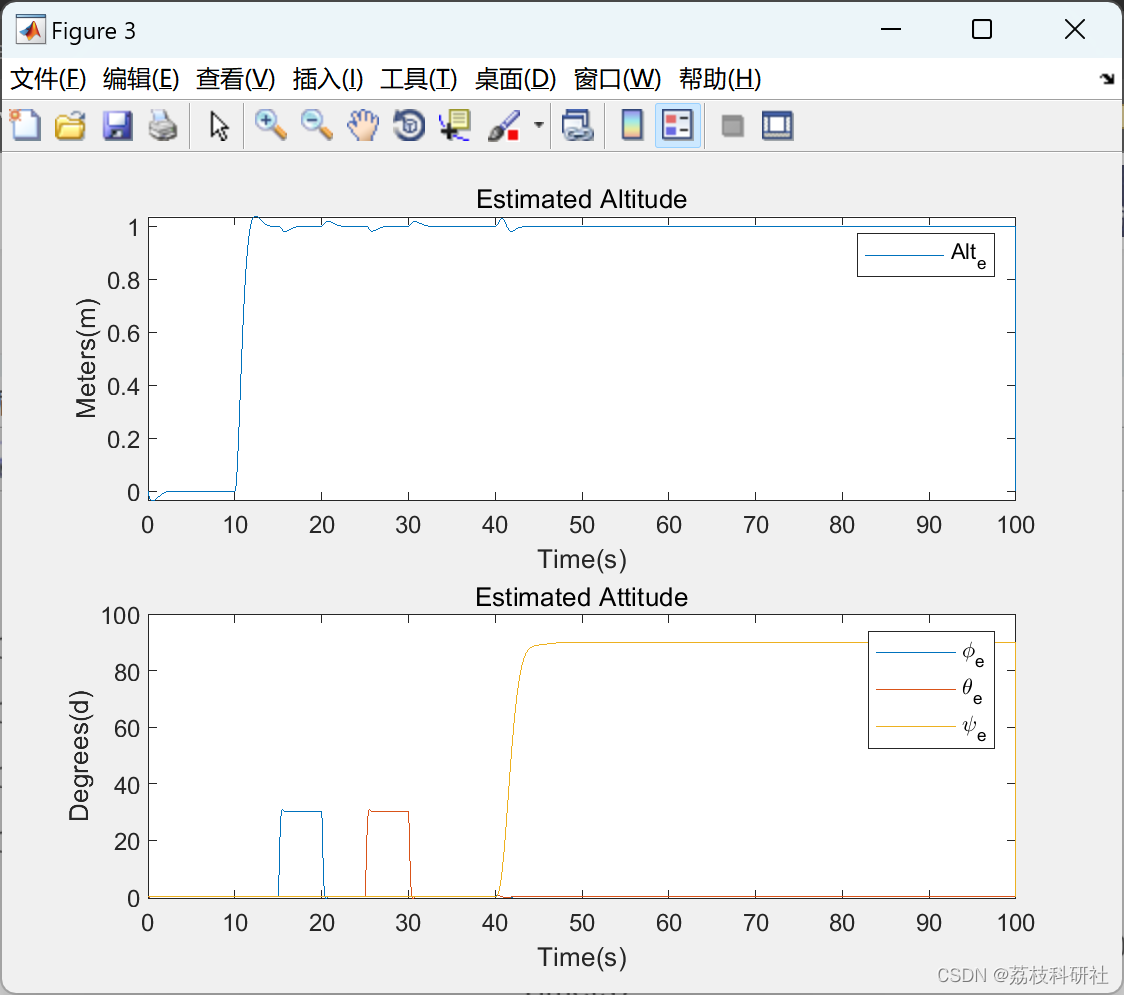
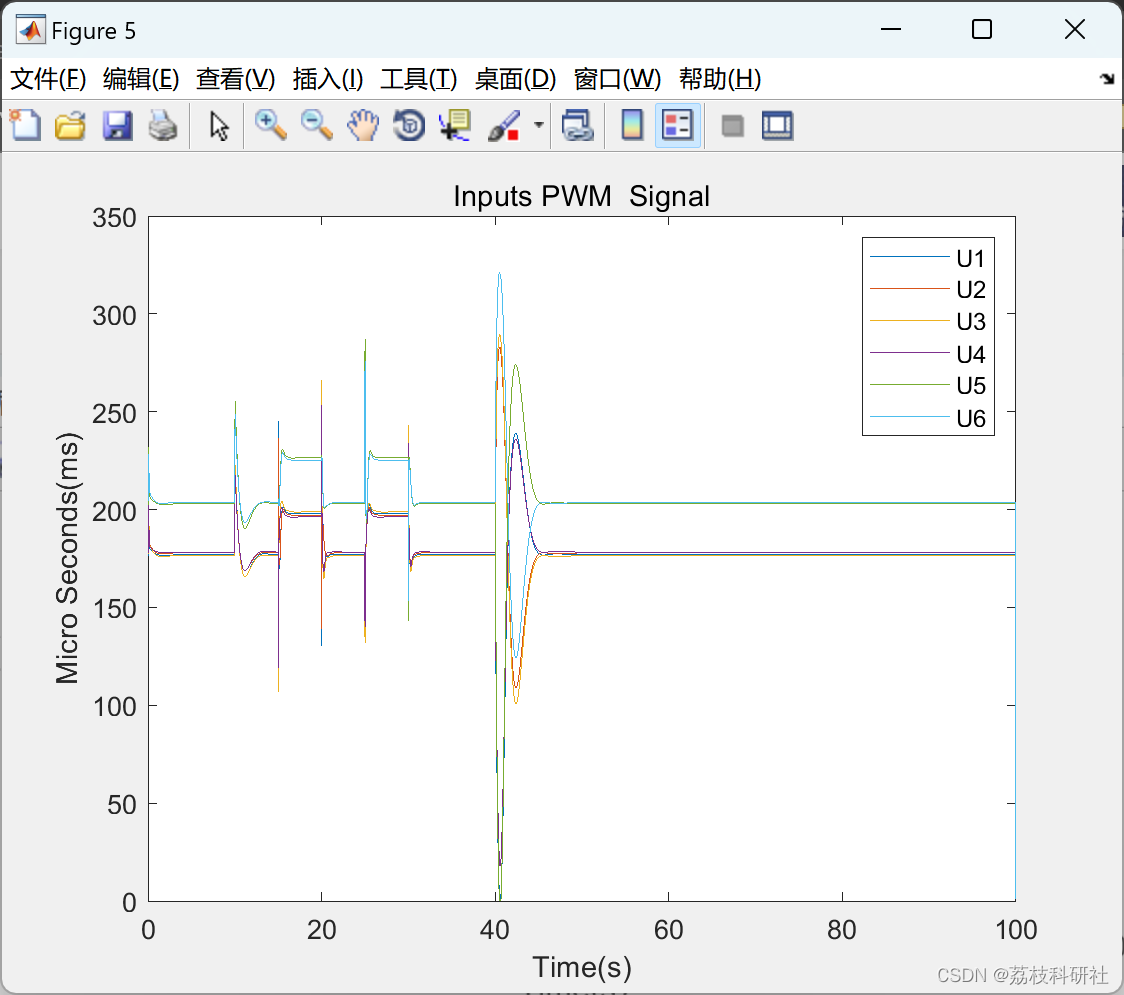
部分代码：

close all; % close all figures
clear; % clear workspace variables
clc; % clear command window
format short;

%% Mass of the Multirotor in Kilograms as taken from the CAD

M = 1.455882;
g = 9.81;

%% Dimensions of Multirotor

L1 = 0.19; % along X-axis Distance from left and right motor pair to center of mass
L2 = 0.18; % along Y-axis Vertical Distance from left and right motor pair to center of mass
L3 = 0.30; % along Y-axis Distance from motor pair to center of mass

%% Mass Moment of Inertia as Taken from the CAD

Ixx = 0.014;
Iyy = 0.028;
Izz = 0.038;

%% Motor Thrust and Torque Constants (To be determined experimentally)