足式机器人的全身模型预测控制

kuan_li_lyg

已于 2025-05-11 11:28:48 修改

阅读量1.2k

点赞数 11

文章标签：机器人 matlab 开发语言算法 stm32 python 人工智能

于 2025-05-11 06:00:00 首次发布

本文链接：https://blog.csdn.net/weixin_46300916/article/details/147854353

版权

系列文章目录

5.1 面向真实世界足式机器人的交互式图形用户界面

前言

我们展示了一种非常简单的四足机器人和仿人机器人全身模型预测控制 (MPC) 方法在现实世界中的惊人效果：采用 MuJoCo 动力学和有限差分近似导数的迭代 LQR (iLQR) 算法。在仿真中使用 MuJoCo 对运动和操作任务进行基于模型的行为合成和控制取得成功的基础上，我们表明这些策略可以很容易地推广到现实世界中，几乎不需要考虑仿真到真实的问题。我们的基线方法在各种硬件实验中实现了实时全身 MPC，包括动态四足运动、四足双腿行走和全尺寸仿人双足运动。我们希望这一易于生产的硬件基线能降低现实世界中全身 MPC 研究的入门门槛，并有助于加快社区的研究速度。

一、导言

让足式机器人实现人类和动物级别的敏捷性是机器人研究人员几十年来一直面临的挑战。除了其他非足式移动机器人（如无人机、自动驾驶汽车等）所面临的挑战外，足式系统一般都是高维的，必须有效地推理与世界的接触和断开。基于模型的控制[1, 2]和强化学习（RL）[3, 4]方法的进步在过去 10-15 年间释放了足式机器人的巨大野外能力。同期，机器人仿真在物理精度[5, 6, 7]、可微分性[7, 8]和并行化性能[6, 8, 9]等方面也取得了显著的发展。得益于仿真技术的这些进步，再加上更广泛的机器学习社区（如 PyTorch [10] 和 JAX [11]）所支持的令人难以置信的工具，仿真到真实的 RL 已获得加速进展，并成为解决人形全身控制等挑战性问题的标准方法。有趣的是，相比之下，基于模型的控制研究人员通常更青睐新颖、定制的机器人模型实现[7, 12]和优化求解器[13, 14, 15]，部分原因是模型预测控制（MPC）范式的在线计算要求，使得这些工作相对更难复制，到目前为止，社区采用的速度较慢。

图 1：Unitree Go1 四足机器人使用 MuJoCo iLQR 策略从四足模式过渡到手倒立模式（上排），并用后腿行走（下排）。

本文旨在通过提供基于 MuJoCo 物理引擎[6]（一种标准、易用的开源机器人仿真器）的开源基准 MPC 算法和足式机器人实际实现来缩小这一差距。我们的研究表明，基于 MuJoCo 的标准梯度 MPC 算法，尤其是迭代 LQR（iLQR）算法，竟然能够实时解决各种具有挑战性的现实世界任务，例如四足和全尺寸仿人机器人的双足运动。我们希望这一努力能降低足式机器人硬件基于模型的进一步控制研究的准入门槛，并最终带来加速的研究动力。

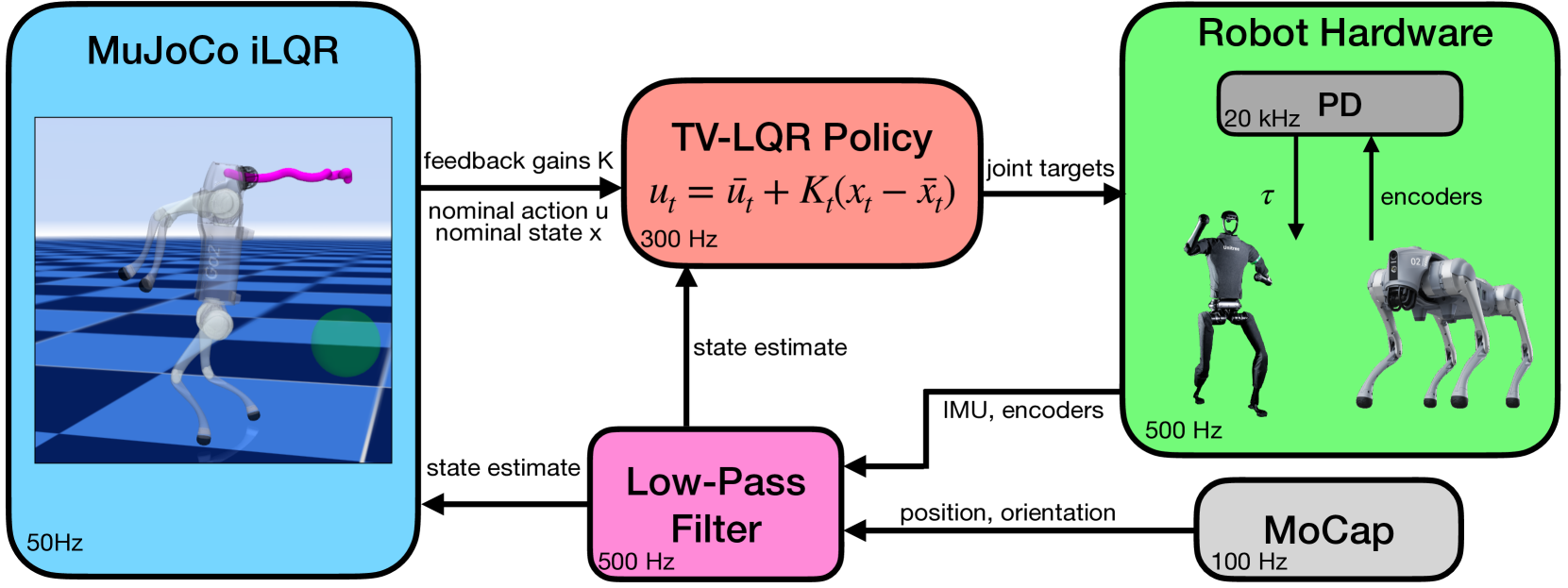
图 2：在 Unitree 四足机器人和仿人机器人上部署 MuJoCo iLQR 策略的系统图。iLQR 算法以 50 Hz 的频率提供控制、状态和时变 LQR（TV-LQR）反馈增益轨迹。TV-LQR 反馈策略可在 300 Hz 频率下更新，并传递给联合级 PD 控制器。机器人的状态是通过融合板载关节编码器和运动捕捉数据来估计的。实时状态估计以 300-500 Hz 的频率在规划器中更新，并在 MuJoCo MPC GUI 中可视化。成本类别是离线设计的，但相对权重、目标位置和 iLQR 超参数可由用户通过图形用户界面进行实时交互式调整。

我们在本文中的具体贡献是

一种用于真实世界足式机器人运动的简单但出人意料地有效的基准全身预测控制算法。
用于真实世界足式机器人预测控制的开源交互式图形用户界面系统。
一组硬件实验，证明基线算法在四足机器人和仿人机器人上执行各种任务时的有效性。

本文的其余部分安排如下：在第二节中，我们首先回顾了 iLQR、全身 MPC 以及基于模型控制的开源工作的相关文献。接下来，我们将在第三节简要介绍 MuJoCo 接触模型和 iLQR，然后在第四节介绍将 iLQR 策略转移到硬件的关键注意事项和实施细节。最后，我们在第六部分讨论了系统目前的局限性和未来的工作方向。

二、背景和相关工作

本节简要回顾了 iLQR 算法，调查了足式机器人 MPC 的相关文献，以及为改进基于模型控制的工具而做出的其他显著努力。

2.1 ILQR

微分动态规划（Differential Dynamic Programming，DDP）最初是在 [16] 中提出的，用于解决以下非线性轨迹优化问题：

通过迭代泰勒展开到二阶，并用动态规划法求解得到的近似问题。除了标称控制序列 u0T- 外，DDP 还会产生一个时变线性反馈策略：

其中 u¯ 和 x¯ 为当前解，Kt 为时间索引 t 时的反馈增益矩阵，k 为对当前控制的改进，α 为直线搜索步长。这种单次搜索公式只对控制 u0:T1 进行优化，并通过对离散时间动态 x 和 T 分别是运行成本和终端成本进行积分来恢复相应的状态 x0T。在每次迭代中，成本和动态与控制序列的导数都会在当前解点附近计算，这一过程称为线性化，以形成一个具有二次成本和线性约束的子问题。术语迭代 LQR [17, 18] 或 iLQR 通常指原始 DDP 算法的高斯-牛顿近似值，通常计算效率更高。iLQR 算法还可以进行修改，以处理控制限制 [19]、状态约束 [13, 15] 和接触 [20]。

作为一种单射算法，iLQR 可保持动态可行的状态轨迹，且无收敛要求，适合热启动，并能自然处理不稳定系统，因为滚动是通过反馈策略执行的，所有这些特点都使其成为一种有吸引力的在线控制器。然而，这种方法通常假定动力学是平滑和可微分的。对于有接触的机器人来说，动力学是非光滑的，导数的计算也变得不容易 [7, 21]。我们的实证结果表明，MuJoCo 软接触模型及其有限差分导数近似值的组合足以满足 iLQR 的要求，而且令人惊讶的是，尽管存在明显的模型不匹配，它仍能很好地移植到机器人硬件上。

图 3：用于在硬件上部署足式机器人的 MuJoCo MPC 图形用户界面。通过该图形用户界面，用户可以改变绿色球体所定义的目标位置，从而交互式地控制真实世界中的机器人。此外，用户还可以更新规划器代理参数，并实时观察仿真状态和真实世界中的机器人行为。

2.2 足式机器人的全身 MPC

全身非线性 MPC 对足式机器人提出了挑战，主要是因为推理可能的接触模式和计算高自由度动力学及其导数的实时性要求很高。传统上，实时 MPC 是通过简化模型 [14, 22] 和启发式选择接触模式 [22, 23] 来实现的。较早的全身 MPC 研究已应用于仿人机器人 [24]，但它们通常达不到在线控制器的实时要求，限制了其在现实世界中的应用能力。得益于计算机性能的进步和动力学库实施的日益成熟[25]，近年来实时全身 MPC 在四足机器人[26, 27]和仿人机器人[28]上的可计算性大大提高。另一个有趣的研究方向是探索通过 GPU 并行化实现全身 MPC [29]，但迄今为止仅限于模型的单一动力学线性化。

不过，这些方法一般都需要定制机器人动力学建模、非连续接触动力学的非难分析导数以及定制优化求解器才能实时运行，这使得这些先前的工作难以复制和迭代。本文展示了一种更简单、更直接的方法，即使用现成的仿真器对机器人进行建模，并通过有限差分对导数进行近似，这种方法对于没有指定接触模式的四足和仿人运动也非常有效。

2.3 基于模型控制的开源工具

必须承认以前为加速基于模型的控制所做的开源努力。其中，MuJoCo MPC [30] 实现了多种基于导数和无导数的预测控制算法，并在仿真中展示了其有效性。[31, 32]利用 MuJoCo 动力学在开环稳定任务（如四足行走）上成功演示了基于采样的 MPC 的模拟到实际的转移。与[31]类似，本研究以[30]为基础，重点关注基于导数的迭代 LQR（iLQR）算法的模拟到现实。与基于采样的 MPC 不同，我们展示了 iLQR 能够成功解决双足行走等固有的开环不稳定任务。

在 MuJoCo 生态系统之外，Pinocchio [25] 已成为社区中高效计算刚体动力学及其导数的流行工具箱。该动力学工具箱还支持各种非线性轨迹优化库[33, 34]，专为足式运动等富于接触的机器人任务而设计。此外，Drake[5] 还提供了建模功能，可解决精确的接触和摩擦动力学问题，但却要为基于模型的控制和验证付出高昂的计算成本。

三、使用 MuJoCo 的迭代 LQR

本节简要介绍了 MuJoCo 软接触模型、MuJoCo MPC 工具箱、MuJoCo iLQR 实现的细节以及模拟到实际的注意事项。

3.1 软接触模型和导数

MuJoCo 物理引擎实现了软接触模型，该模型是对非凸、不连续接触和摩擦模型的凸近似。虽然物体之间的相互渗透现象（例如机器人的脚和地板）在物理上可能被认为是不现实的，但这种凸表述快速、高效，并能提供有保证的解决方案，这在解决非凸问题时是很难做到的。此外，从理论上讲，软接触模型通过接触提供了平滑的导数。虽然尚未提供分析导数，但只需从原始的时间步进仿真问题中花费很少的额外精力，就能计算出有限不同的导数。

为了逼近模型导数，我们使用了正向差分法 fϵ，因为与居中差分法 fϵ 中的两个维度相比，正向差分法每个维度只需额外进行一次仿真评估，其中 f 是输入 x 的任意函数，ϵ 是有限差分容差。

3.2 MuJoCo iLQR

我们以开源的 MuJoCo MPC [30] 工具箱为基础，该工具箱实现了第 2.1 章所述的 iLQR 算法，并部署在 Unitree 四足机器人和仿人机器人上（图 2）。由于在线运动规划的性质，我们在返回当前最佳标称轨迹和反馈策略之前，先求解一次 iLQR 迭代，而不进行收敛检查。然后，利用机器人提供的新状态信息，利用该解决方案温启动下一次迭代。此外，我们还实现了正则化和并行寻线等附加功能。

图 4：左上：四足机器人原地站立时两种印模接触设置的大腿关节控制轨迹。默认设置导致非物理性的脚部滑动和生涩的控制（红线），对硬件有潜在危险。右上图：增加印迹率可避免这一问题（蓝线），但会增加计算时间（右上图）。每个条形图的 1 标准差置信区间以黑色显示。底部：每种设置下 iLQR 不同组件的时序分解。

四、部署细节

本节记录了在硬件上成功部署实时 MuJoCo iLQR 的几个实施细节。

4.1 接触建模

虽然 MuJoCo 默认的接触参数既快速又符合物理原理，但由于求解器无法强制执行摩擦约束，因此也经常导致接触滑动[35]。这种来自规划器模型的滑动动态会导致生涩的控制轨迹（图 4 左上角），难以在硬件上执行。为了解决这一问题，我们将解算器在滑动与穿透之间进行权衡的能力（大致对应于解算器的 impratio 值）从默认的 1 提高到 100。这一变化也增加了仿真问题的求解时间，并因此增加了 iLQR 的迭代时间。对于我们的四足系统，在第 12 代英特尔 i7 CPU 上，单次 iLQR 迭代时间从 10 毫秒增加到 20 毫秒。在实际部署过程中，我们发现增加的计算时间并不是问题。有趣的是，根据我们的经验，接触模型的软性所产生的适度地面穿透并不会在模拟到实际的传输过程中造成问题。

图 5：在硬件上执行 H1 人形机器人小跑任务时，在标称控制序列中应用 iLQR 政策（蓝色）和不应用 TV-LQR 反馈增益（红色）的成本比较。TV-LQR 策略可将任务性能提高 30%。

4.2 执行器阻抗

MuJoCo 仿真可以轻松地以定义明确的单位定义关节级阻抗。然而，据我们所知，真实世界中机器人的阻抗参数是以黑盒单位提供的，这就导致了非同小可的模型不匹配。我们通过手动调整为每个机器人解决了这一问题，但更系统化的识别关节级系统动态的方法对于在不冒损坏风险的情况下最大限度地提高机器人能力至关重要。

4.3 时变线性反馈

我们比较了 iLQR 策略在有 TV-LQR 反馈和无 TV-LQR 反馈情况下在 H1 人形机器人原地小跑任务中的实际表现。与直接在机器人上执行名义开环控制序列相比，TV-LQR 策略提高了任务性能，但幅度很小，在 8 秒的窗口内平均提高了 30% 的跟踪性能（图 5）。请注意，图 5 中红线（无反馈）中 1.5 秒左右的成本峰值表明，在龙门架支持下恢复的策略暂时失效。有反馈策略的试验在同一窗口内没有失败。我们的经验结果与之前的研究结果一致[36]，后者表明平滑动态的线性反馈对于稳定接触丰富的计划似乎并不理想。

4.4 导数逼近

计算每个节点上的动力学导数通常是 iLQR 中计算成本最高的步骤（图 4）。我们采用了一种可选的启发式方法，即跳过规划范围内某些结点的动态导数评估，而是从附近的评估结果中进行插值。采用这种启发式的原因是，机器人的动态近似于局部线性，因此附近节点之间的变化不大[37]。这在图形用户界面中以 skip_deriv 的形式实现，其中整数值对应的是在计算下一个导数之前要跳过的节点数。在本文所考虑的任务中，我们发现 iLQR 更新频率与 TV-LQR 策略配对后已经足够。不过，在更多的铰接系统上或计算能力有限的情况下，这种选择仍然有利于实时启用 iLQR。

需要注意的是，虽然出于计算方面的考虑，我们选择使用正向差分近似法，但我们发现居中差分法在运动任务中并不适用，即使在没有实时性要求的仿真中也是如此。我们推测，在运动过程中，进入接触点的导数信息（在负高度方向扰动机器人状态时可能会出现这种情况）并不具有参考价值，但我们会在今后的工作中进一步研究。

五、实验和结果

本节将介绍机器人硬件平台上的交互式图形用户界面设置以及各种硬件实验。在第 V-B 节中，我们首先演示了我们的系统在 Go1 和 Go2 机器人上的基本四足运动。接下来，我们将在第 V-C 节中展示 MuJoCo iLQR 可自然扩展到开环不稳定任务，如四足式双腿行走。最后，我们将在第 V-D 节中把我们的系统部署在一个与人一样大小的 Unitree H1 人形机器人上。

5.1 面向真实世界足式机器人的交互式图形用户界面

我们通过 Python 与 MuJoCo MPC 图形用户界面和 iLQR 计划器连接，进行机器人硬件部署。该界面接收最新的状态估计和当前控制。状态估计是通过 ROS 以 100Hz 频率融合 Optitrack MoCap [38] 位置和姿态测量值，以及以 500Hz 频率融合机器人关节角度位置和速度测量值计算得出的。通过对位置和姿态测量值的有限差分值应用低通滤波器，计算出身体框架中的浮动基线速度和角速度。Go1 机器人通过 Unitree SDK，Go2 和 H1 机器人通过 Unitree SDK 2，将规划器的行动传达给机器人。所有的机器人控制都表示为联合目标，并使用 Unitree 内部的低级 PD 控制器进行跟踪。我们在配备有 20 个内核的第 13 代英特尔 i9 CPU 芯片的台式机上计算 MPC 策略，该 CPU 与本文前面提到的不同。我们以 ∼50 Hz 的频率更新 iLQR 策略，并使用 TV-LQR 策略在两次求解之间以 ∼300 Hz 的频率稳定机器人。除非另有说明，我们使用 0.35s 的默认预测时间跨度，并在 iLQR 规划器中以 100Hz 的频率进行动态离散。

由于 MPC 规划器是用 C++ 实现并异步更新的，因此使用 Python 接口不会影响规划频率。虽然我们观察到 Python API 会带来 3ms 的消息传递开销，但对于本文介绍的任务而言，规划器对这种未建模的延迟具有很强的鲁棒性。

5.2 四足运动

我们首先使用一个简单的四足运动任务来验证我们的系统。该任务旨在让机器人按照参考步态行走到目标位置。我们成功地将策略部署到带有 12 自由度 (DoF) 关节致动器的 Unitree Go1 和 Go2 机器人上。如图 3 所示，图形用户界面允许用户交互式移动目标，现实世界中的机器人可以跟随虚拟目标移动。请注意，虽然我们在规划器模型中保留了全身碰撞的几何形状，但在考虑的运动任务中，一般只有 4 个球形接触点处于活动状态。

5.3 四足机器人的双足运动

接下来，我们将展示 iLQR 策略可以自然处理开环不稳定任务，例如四足式机器人用两条足行走（图 1）。相比之下，MPPI[31]可以处理稳定的运动任务，但在动态不稳定的情况下就会失效，例如在双足行走时。在图 1 中，我们利用 MuJoCo iLQR 策略，成功地让一个四足机器人仅靠后腿优雅地行走，同时利用前腿保持平衡，并从初始的四足构型起身摆出手立姿势。

5.4 人形机器人运动

最后，我们在 H1 全尺寸仿人机器人上部署了 iLQR 策略，以跟踪周期性小跑步态，如图 6 所示。与图 3 中的四足运动任务类似，我们要求机器人走到一个定义为绿色球体的位置。为了在更复杂的系统上实现实时控制，我们关闭了机器人身体上除每只脚上两个球形接触点以外的碰撞检查功能。此外，我们还禁用了机器人上半身的 DoFs，因为这些 DoFs 只配备了相对编码器，无法提供可靠的关节角度估计，因为它们对运动并不重要。虽然这减少了 iLQR 的计算时间，但我们认为这对任务的成功并无必要。总的来说，该系统有 10 个 DoF 关节致动器和 4 个接触点。我们使用的预测时间跨度为 0.5 秒。

图 6：使用 MuJoCo iLQR 的 Uniree H1 机器人在原地小跑。

六、结论与未来工作

我们介绍了一种使用 MuJoCo 实现四足机器人和仿人机器人全身 MPC 的非常简单但能力惊人的方法。我们希望，通过利用广泛采用的物理引擎对这一基线方法进行成功的硬件验证，能够鼓励研究人员利用现有工具开展基于模型的控制研究。尽管取得了可喜的成果，但未来的工作仍存在几个关键的局限性。

首先，可靠的状态估计仍然是足式机器人基于模型的规划和控制所面临的关键挑战。因此，许多研究人员更倾向于使用 RL 范式，因为这种范式很容易支持直接从传感器测量的历史记录中学习控制策略。我们目前的系统依靠基于标记的运动捕捉来获得良好的机器人位置测量结果。未来的工作应开发易于使用的工具，以便仅通过机器人的板载传感器进行全状态估计，使我们的机器人能够在受控的实验室环境外行走。其次，研究界还需要更多的工具来对机器人的关节执行和接触动力学进行严格的系统识别，以克服模拟与现实之间的巨大差距。

iLQR 算法还存在一些基本限制。首先，iLQR 难以探索接触模式。作为一种基于二阶导数的局部计划器，iLQR 在任务规范（成本函数）中提供了参考接触模式计划时表现出色，这通常是运动的情况。不过，对于接触更多的全身运动操作任务，基于无导数采样的方法在发现有用的接触模式方面表现得更有前途，而无需预先指定[31]。此外，iLQR 的滚动和后退都是基本的串行操作。随着多核 CPU 和大规模并行 GPU 的兴起，计算机的并行化程度越来越高，因此研究能够利用这种计算模式的 MPC 算法变得越来越重要。最后，iLQR 还存在其他与其单射性质相关的问题，如对初始猜测的敏感性、数值不稳定性和较长时间内收敛性差等。未来的工作应扩展当前的 MPC 库，使社区更容易使用多重射击和拼位方法。

References

[1]↑R. Deits, S. Kuindersma, M. P. Kelly, T. Koolen, Y. Abe, and B. Stephens, “Robot movement and online trajectory optimization,” U.S. patent 11 833 680, 12 5, 2023, uS Patent 11,833,680. [Online]. Available: https://patents.google.com/patent/US11833680B2/
[2]↑R. Grandia, F. Jenelten, S. Yang, F. Farshidian, and M. Hutter, “Perceptive locomotion through nonlinear model-predictive control,” IEEE Transactions on Robotics, vol. 39, no. 5, pp. 3402–3421, 2023.
[3]↑J. Lee, M. Bjelonic, A. Reske, L. Wellhausen, T. Miki, and M. Hutter, “Learning robust autonomous navigation and locomotion for wheeled-legged robots,” Science Robotics, vol. 9, no. 89, p. eadi9641, 4 2024.
[4]↑D. Hoeller, N. Rudin, D. Sako, and M. Hutter, “Anymal parkour: Learning agile navigation for quadrupedal robots,” Science Robotics, vol. 9, no. 88, p. eadi7566, 3 2024.
[5]↑R. Tedrake and the Drake Development Team, “Drake: Model-based design and verification for robotics,” 2019. [Online]. Available: https://drake.mit.edu
[6]↑E. Todorov, T. Erez, and Y. Tassa, “Mujoco: A physics engine for model-based control,” in 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2012, pp. 5026–5033.
[7]↑T. Howell, S. Le Cleac’h, J. Bruedigam, Z. Kolter, M. Schwager, and Z. Manchester, “Dojo: A differentiable physics engine for robotics,” arXiv preprint arXiv:2203.00806, 2022. [Online]. Available: https://arxiv.org/abs/2203.00806
[8]↑M. Macklin, “Warp: A high-performance python framework for gpu simulation and graphics,” https://github.com/nvidia/warp, March 2022, nVIDIA GPU Technology Conference (GTC).
[9]↑N. Rudin, D. Hoeller, P. Reist, and M. Hutter, “Learning to walk in minutes using massively parallel deep reinforcement learning,” 2022. [Online]. Available: [2109.11978] Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning
[10]↑A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai, and S. Chintala, “Pytorch: An imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems 32, H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett, Eds. Curran Associates, Inc., 2019, pp. 8024–8035. [Online]. Available: http://papers.neurips.com/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf
[11]↑J. Bradbury, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne, and Q. Zhang, “JAX: composable transformations of Python+NumPy programs,” 2018. [Online]. Available: http://github.com/jax-ml/jax
[12]↑J. Carpentier, L. Montaut, and Q. L. Lidec, “From compliant to rigid contact simulation: a unified and efficient approach,” 2024. [Online]. Available: [2405.17020] From Compliant to Rigid Contact Simulation: a Unified and Efficient Approach
[13]↑T. A. Howell, B. E. Jackson, and Z. Manchester, “Altro: A fast solver for constrained trajectory optimization,” in 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019.
[14]↑S. Le Cleac’h, T. A. Howell, S. Yang, C.-Y. Lee, J. Zhang, A. Bishop, M. Schwager, and Z. Manchester, “Fast contact-implicit model predictive control,” IEEE Transactions on Robotics, vol. 40, pp. 1617–1629, 2024.
[15]↑W. Jallet, A. Bambade, E. Arlaud, S. El-Kazdadi, N. Mansard, and J. Carpentier, “Proxddp: Proximal constrained trajectory optimization,” arXiv preprint, 2023, preprint submitted on 8 Dec 2023.
[16]↑D. H. Jacobson and D. Q. Mayne, Differential Dynamic Programming. Elsevier, 1970.
[17]↑Y. Tassa, T. Erez, and E. Todorov, “Synthesis and stabilization of complex behaviors through online trajectory optimization,” in IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2012, pp. 4906–4913.
[18]↑W. Li and E. Todorov, “Iterative linear quadratic regulator design for nonlinear biological movement systems,” in Proceedings of the 1st International Conference on Informatics in Control, Automation and Robotics, 2004.
[19]↑Y. Tassa, N. Mansard, and E. Todorov, “Control-limited differential dynamic programming,” in IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2014, pp. 1168–1175.
[20]↑N. J. Kong, C. Li, G. Council, and A. M. Johnson, “Hybrid ilqr model predictive control for contact implicit stabilization on legged robots,” IEEE Transactions on Robotics, vol. 39, no. 6, pp. 4712–4727, 2023.
[21]↑N. J. Kong, J. Joe Payne, J. Zhu, and A. M. Johnson, “Saltation matrices: The essential tool for linearizing hybrid dynamical systems,” Proceedings of the IEEE, vol. 112, no. 6, pp. 585–608, 2024.
[22]↑G. Bledt, M. J. Powell, B. Katz, J. Di Carlo, P. M. Wensing, and S. Kim, “Mit cheetah 3: Design and control of a robust, dynamic quadruped robot,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2018, pp. 2245–2252.
[23]↑M. H. Raibert and H. B. Brown, “Dynamically stable legged locomotion,” 1983.
[24]↑J. Koenemann, A. Del Prete, Y. Tassa, E. Todorov, O. Stasse, M. Bennewitz, and N. Mansard, “Whole-body model-predictive control applied to the hrp-2 humanoid,” in 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2015, pp. 3346–3351.
[25]↑J. Carpentier, G. Saurel, G. Buondonno, J. Mirabel, F. Lamiraux, O. Stasse, and N. Mansard, “The pinocchio c++ library – a fast and flexible implementation of rigid body dynamics algorithms and their analytical derivatives,” in IEEE International Symposium on System Integrations (SII), 2019.
[26]↑G. Kim, D. Kang, J.-H. Kim, S. Hong, and H.-W. Park, “Contact-implicit model predictive control: Controlling diverse quadruped motions without pre-planned contact modes or trajectories,” The International Journal of Robotics Research, Oct. 2024. [Online]. Available: Contact-implicit Model Predictive Control: Controlling diverse quadruped motions without pre-planned contact modes or trajectories
[27]↑G. Lunardi, T. Corbères, C. Mastalli, N. Mansard, T. Flayols, S. Tonneau, and A. D. Prete, “Reference-free model predictive control for quadrupedal locomotion,” IEEE Access, vol. 12, pp. 689–698, 2024.
[28]↑C. Khazoom, S. Hong, M. Chignoli, E. Stanger-Jones, and S. Kim, “Tailoring solution accuracy for fast whole-body model predictive control of legged robots,” IEEE Robotics and Automation Letters, vol. 9, no. 12, pp. 11 074–11 081, 2024.
[29]↑A. L. Bishop, J. Z. Zhang, S. Gurumurthy, K. Tracy, and Z. Manchester, “Relu-qp: A gpu-accelerated quadratic programming solver for model-predictive control,” in 2024 IEEE International Conference on Robotics and Automation (ICRA), 2024, pp. 13 285–13 292.
[30]↑T. Howell, N. Gileadi, S. Tunyasuvunakool, K. Zakka, T. Erez, and Y. Tassa, “Predictive Sampling: Real-time Behaviour Synthesis with MuJoCo,” dec 2022. [Online]. Available: [2212.00541] Predictive Sampling: Real-time Behaviour Synthesis with MuJoCo
[31]↑J. Alvarez-Padilla, J. Z. Zhang, S. Kwok, J. M. Dolan, and Z. Manchester, “Real-time whole-body control of legged robots with model-predictive path integral control,” arXiv preprint arXiv:2409.10469, 2024, available at: [2409.10469] Real-Time Whole-Body Control of Legged Robots with Model-Predictive Path Integral Control.
[32]↑H. Xue, C. Pan, Z. Yi, G. Qu, and G. Shi, “Full-order sampling-based mpc for torque-level locomotion control via diffusion-style annealing,” 2024. [Online]. Available: [2409.15610] Full-Order Sampling-Based MPC for Torque-Level Locomotion Control via Diffusion-Style Annealing
[33]↑W. Jallet, A. Bambade, S. El Kazdadi, C. Justin, and M. Nicolas, “aligator.” [Online]. Available: https://github.com/Simple-Robotics/aligator
[34]↑C. Mastalli, R. Budhiraja, W. Merkt, G. Saurel, B. Hammoud, M. Naveau, J. Carpentier, L. Righetti, S. Vijayakumar, and N. Mansard, “Crocoddyl: An Efficient and Versatile Framework for Multi-Contact Optimal Control,” in IEEE International Conference on Robotics and Automation (ICRA), 2020.
[35]↑MuJoCo Team, “Preventing slip - MuJoCo documentation,” Modeling - MuJoCo Documentation, 2023, accessed: 2025-02-25.
[36]↑Y. Shirai, T. Zhao, H. J. T. Suh, H. Zhu, X. Ni, J. Wang, M. Simchowitz, and T. Pang, “Is linear feedback on smoothed dynamics sufficient for stabilizing contact-rich plans?” 2024. [Online]. Available: [2411.06542] Is Linear Feedback on Smoothed Dynamics Sufficient for Stabilizing Contact-Rich Plans?
[37]↑D. Han, H. Eom, J. Noh, and J. S. Shin, “Data-guided model predictive control based on smoothed contact dynamics,” Computer Graphics Forum, vol. 35, no. 2, pp. 533–542, May 2016, (formerly Sung Yong Shin).
[38]↑“Optitrack motion capture system,” 2025, available at: https://www.optitrack.com.