一、简介
- 点到点的轨迹规划算法可以理解为在规定的时间T内,从已知起始点
Θ
s
t
a
r
t
{\Theta_{start}}
Θstart运动到末尾点
Θ
e
n
d
{\Theta_{end}}
Θend的方法。这里引入中间变量
s
(
t
)
s(t)
s(t),它是时间的函数,定义域为
[
0
,
T
]
[0,T]
[0,T],值域为
[
0
,
1
]
[0,1]
[0,1],
s
s
s与
Θ
{\Theta}
Θ的关系见下面公式。
这个公式不难理解,当 s = 0 {s=0} s=0时, Θ = Θ e n d {\Theta = \Theta_{end}} Θ=Θend; 当 s = 1 {s=1} s=1时 Θ = Θ e n d {\Theta = \Theta_{end}} Θ=Θend 。
θ ( s ) = θ s t a r t + s ( θ e n d − θ s t a r t ) s ϵ [ 0 , 1 ] s = s ( t ) , t ϵ [ 0 , T ] {{\theta(s)=\theta_{start} + s( \theta_{end}-\theta_{start})s\epsilon [0,1]} \ \ \ \ \ \ {s = s(t),t\epsilon[0,T]}} θ(s)=θstart+s(θend−θstart)sϵ[0,1] s=s(t),tϵ[0,T]
Θ \Theta Θ对 t t t求导,即有:
∂ θ ∂ t = ∂ θ ∂ s . ∂ s ∂ t 其 中 , ∂ θ ∂ s = θ e n d − θ s t a r t {\frac{\partial \theta}{\partial t} = \frac{\partial \theta}{\partial s}. \frac{\partial s}{\partial t} \ \ 其中, \frac{\partial \theta}{\partial s} = \theta_{end}-\theta_{start} } ∂t∂θ=∂s∂θ.∂t∂s 其中,∂s∂θ=θend−θstart
因此可得:
∂ θ ∂ t = ( θ e n d − θ s t a r t ) . ∂ s ∂ t {\frac{\partial \theta}{\partial t} =(\theta_{end}-\theta_{start} ). \frac{\partial s}{\partial t}} ∂t∂θ=(θend−θstart).∂t∂s
Θ \Theta Θ 对 t t t求二阶倒数,有
∂ 2 θ ∂ 2 t = ( θ e n d − θ s t a r t ) . ∂ 2 s ∂ 2 t {\frac{\partial^2 \theta}{\partial^2 t} =(\theta_{end}-\theta_{start} ). \frac{\partial^2 s}{\partial^2 t}} ∂2t∂2θ=(θend−θstart).∂2t∂2s
由于, Θ s t a r t {\Theta_{start}} Θstart和, Θ e n d {\Theta_{end}} Θend是已知的,所以速度和加速度随时间的变化取决于 s = s ( t ) , t ϵ [ 0 , T ] s=s(t), t\epsilon[0,T] s=s(t),tϵ[0,T],这里的 s ( t ) s(t) s(t)有很多种方法,比较常用的是三次函数,五次函数,梯形曲线,S曲线等。这里对这几种曲线的方法和优缺点进行一下介绍。
二、曲线
2.1. 三次曲线
三次曲线的公式为
s
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
s(t)=a_0+a_1t+a_2t^2+a_3t^3
s(t)=a0+a1t+a2t2+a3t3
根据起始和终止时刻的约束条件,
s
(
0
)
=
0
,
s
(
T
)
=
1
,
s
˙
(
0
)
=
0
,
s
¨
(
T
)
=
0
{s(0)=0,s(T)=1,\ \dot{s}(0)=0,\ \ddot{s}(T)=0}
s(0)=0,s(T)=1, s˙(0)=0, s¨(T)=0
即可得出三次曲线的参数:
a
0
=
0
,
a
1
=
0
,
a
2
=
3
T
2
,
a
3
=
−
2
T
3
a_0=0,a_1=0,a_2=\frac{3}{T^2},a_3=-\frac{2}{T^3}
a0=0,a1=0,a2=T23,a3=−T32
所以:
s
(
t
)
=
3
T
2
t
2
−
2
T
3
t
3
s(t)=\frac{3}{T^2}t^2-\frac{2}{T^3}t^3
s(t)=T23t2−T32t3
分别画出
s
,
s
˙
,
s
¨
s,\ \dot{s},\ \ddot{s}
s, s˙, s¨随时间变化的曲线。可以看出在在初始和末了时刻加速度是不连续的,会有冲击,这也是三次曲线的缺点。

2.2. 五次曲线
五次曲线的公式为:
s
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
+
a
4
t
4
+
a
5
t
5
s(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5
s(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
根据起始和终止时刻的约束条件,
s
(
0
)
=
0
,
s
(
T
)
=
1
,
s
˙
=
0
,
s
¨
(
0
)
=
0
,
s
¨
(
T
)
=
0
{s(0)=0,s(T)=1,\dot{s}=0,\ddot{s}(0)=0,\ddot{s}(T)=0}
s(0)=0,s(T)=1,s˙=0,s¨(0)=0,s¨(T)=0
这六个约束条件可以分别求出:
a
0
=
0
,
a
1
=
0
,
a
2
=
0
,
a
3
=
10
T
3
,
a
4
=
−
15
T
4
,
a
5
=
6
T
5
a_0=0,a_1=0,a_2=0,a_3=\frac{10}{T^3},a_4=-\frac{15}{T^4},a_5=\frac{6}{T^5}
a0=0,a1=0,a2=0,a3=T310,a4=−T415,a5=T56
所以有:
s
(
t
)
=
10
T
3
t
3
−
15
T
4
t
4
+
6
T
5
t
5
s(t)=\frac{10}{T^3}t^3-\frac{15}{T^4}t^4+\frac{6}{T^5}t^5
s(t)=T310t3−T415t4+T56t5
分别画出
s
,
s
˙
,
s
¨
s,\ \dot{s},\ \ddot{s}
s, s˙, s¨随时间变化的曲线。从图中可以看出加速度始末时刻页是连续的,消除了三次曲线始末时刻有冲击的缺点。

2.3 梯形曲线
梯形曲线在电机控制中经常用到,因为
s
˙
\dot {s}
s˙的曲线形状为梯形,所以取名为梯形曲线,见下图。
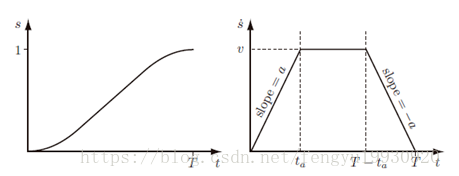
s为分段函数,即
- 0 ⩽ t ⩽ v a : s ( t ) = 1 2 a t 2 0\leqslant t\leqslant \frac{v}{a}:s(t)=\frac{1}{2}at^2 0⩽t⩽av:s(t)=21at2
- v a ⩽ t ⩽ T − v a : s ( t ) = v t − v 2 2 a \frac{v}{a}\leqslant t\leqslant T-\frac{v}{a}:s(t)=vt - \frac{v^2}{2a} av⩽t⩽T−av:s(t)=vt−2av2
- T − v a ⩽ t ⩽ T : s ( t ) = 2 a v T − 2 v 2 − a 2 ( t − T ) 2 ) 2 a T-\frac{v}{a}\leqslant t\leqslant T:s(t)=\frac{2avT - 2v^2-a^2(t-T)^2)}{2a} T−av⩽t⩽T:s(t)=2a2avT−2v2−a2(t−T)2)
这里的v,a,T是有约束条件的,即
s
(
T
)
=
a
v
T
−
v
2
a
=
1
,
t
a
=
v
a
⩽
T
2
,
a
>
0
s(T)=\frac{avT-v^2}{a} = 1 ,t_a=\frac{v}{a}\leqslant \frac{T}{2},a> 0
s(T)=aavT−v2=1,ta=av⩽2T,a>0
因此当指定两个变量,另一个变量即确定,例如
v
,
a
v ,a
v,a,则
T
=
a
+
v
2
v
a
T=\frac{a+v^2}{va}
T=vaa+v2,且
v
2
a
⩽
1
\frac{v^2}{a}\leqslant 1
av2⩽1。
- 梯形加速度控制策略虽然容易实现,但其加速度不连续,在加减速阶段与匀速阶段衔接处存在突变的情况,这会给机器人本体造成冲突。
2.4 S型曲线
- S型曲线算法是工业控制领域另一种常见的加减速控制策略,他将整个运动过程划分为7个阶段,即:加加速阶段,均加速阶段,减加速段,匀速段,加减速段,匀减速段和减减速段,不同阶段速度衔接处加速度连续,且加速度的变化率可控,解决了梯形加减速控制策略存在加速度突变的问题。

它的定义为:
- 第一段:以恒定的痉挛J(加速度的导数)使加速度从0增加到预先设定的a;
- 第二段:以恒定的加速度加速;
- 第三段:**已恒定的负的痉挛J(加速度的导数)**使加速度从预先设定的a减到0;
- 第四段:以恒定的速度v匀速运动;
- 第五段:**已恒定的负的痉挛J(加速度的导数)**使加速度从0减到预先设定的-a;
- 第六段:以恒定的加速度-a减速;
- 第七段:**以恒定的痉挛J(加速度的导数)**使加速度从预先设定的-a增加到0;
在已知最大加速度a, 最大速度v和运行时间T时, 可由以下公式求得s曲线:
J
=
a
2
v
T
f
v
a
−
v
2
−
a
,
t
1
=
a
J
,
t
2
=
v
a
−
a
J
,
t
3
=
a
J
,
t
4
=
2
v
−
T
,
t
5
=
a
J
,
t
6
=
v
a
−
a
J
,
t
7
=
a
J
J= \frac{a^2v}{T_fva-v^2-a},t_1=\frac{a}{J},t_2=\frac{v}{a}-\frac{a}{J},t_3=\frac{a}{J},t_4=\frac{2}{v}-T,t_5=\frac{a}{J},t_6=\frac{v}{a}-\frac{a}{J},t_7=\frac{a}{J}
J=Tfva−v2−aa2v,t1=Ja,t2=av−Ja,t3=Ja,t4=v2−T,t5=Ja,t6=av−Ja,t7=Ja
因此可得这七段中,曲线S 的公式
- 第一段: 0 ⩽ t ⩽ t 1 : s ( t ) = 1 6 J t 3 0\leqslant t\leqslant t_1:s(t)=\frac{1}{6}Jt^3 0⩽t⩽t1:s(t)=61Jt3
- 第二段: t 1 ⩽ t ⩽ t 1 + t 2 : s ( t ) = 1 2 a ( t − t 1 ) 2 + a 2 2 J ( t − t 1 ) + a 3 g J 2 t_1\leqslant t\leqslant t_1+t_2:s(t)=\frac{1}{2}a(t-t_1)^2+\frac{a^2}{2J}(t-t_1)+\frac{a^3}{gJ^2} t1⩽t⩽t1+t2:s(t)=21a(t−t1)2+2Ja2(t−t1)+gJ2a3
- 第三段: t 1 + t 2 ⩽ t ⩽ t 1 + t 2 + t 3 : s ( t ) = 1 6 J ( t − t 1 − t 2 ) 3 + 1 2 a ( t − t 1 − t 2 ) 2 + ( a t 2 + a 2 a J ) ⋅ ( t − t 1 − t 2 ) + 1 2 a t 2 2 + a 2 2 J t 2 + a 3 6 J 2 t_1+t_2\leqslant t\leqslant t_1+t_2+t_3:s(t)=\frac{1}{6}J(t-t_1-t_2)^3+\frac{1}{2}a(t-t_1-t_2)^2+(at_2+\frac{a^2}{aJ})\cdot (t-t_1-t_2)+\frac{1}{2}at_2^2+\frac{a^2}{2J}t_2+\frac{a^3}{6J^2} t1+t2⩽t⩽t1+t2+t3:s(t)=61J(t−t1−t2)3+21a(t−t1−t2)2+(at2+aJa2)⋅(t−t1−t2)+21at22+2Ja2t2+6J2a3
- 第四段: t 1 + t 2 + t 3 ⩽ t ⩽ t 1 + t 2 + t 3 + t 4 : s ( t ) = ( − 1 2 J t 3 + a t 3 + a t 2 + a 2 2 J ) ⋅ ( t − t 1 − t 2 − t 3 ) − 1 6 J t 3 + 1 2 a t 2 + a 2 2 J t 2 + a 3 6 J 2 t_1+t_2+t_3\leqslant t\leqslant t_1+t_2+t_3+t_4:s(t)=(-\frac{1}{2}Jt^3+at_3+at_2+\frac{a^2}{2J})\cdot(t-t_1-t_2-t_3)-\frac{1}{6}Jt^3+\frac{1}{2}at^2+\frac{a^2}{2J}t^2+\frac{a^3}{6J^2} t1+t2+t3⩽t⩽t1+t2+t3+t4:s(t)=(−21Jt3+at3+at2+2Ja2)⋅(t−t1−t2−t3)−61Jt3+21at2+2Ja2t2+6J2a3
- 第五段: t 1 + t 2 + t 3 + t 4 ⩽ t ⩽ t 1 + t 2 + t 3 + t 4 + t 5 : t_1+t_2+t_3+t_4 \leqslant t\leqslant t_1+t_2+t_3+t_4+t_5: t1+t2+t3+t4⩽t⩽t1+t2+t3+t4+t5:
























 1688
1688

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








