1、数学推导
1.0 向量点乘
- 向量点乘(内积)的结果是点积,又称数量积或标量积。
- 在空间中两个向量 a ⃗ = ( x 1 , y 1 , z 1 ) {\vec a =(x_1,y_1,z_1)} a=(x1,y1,z1) , b ⃗ = ( x 2 , y 2 , z 2 ) {\vec b =(x_2,y_2,z_2)} b=(x2,y2,z2),其夹角为 θ {\theta} θ
代数几何:
- 点积是对两个向量对应位置上的值相乘再相加的操作,其结果即为点积
- a ⃗ ⋅ b ⃗ = x 1 x 2 + y 1 y 2 + z 1 z 2 {\vec a \cdot \vec b = x_1x_2+y_1y_2+z_1z_2} a⋅b=x1x2+y1y2+z1z2
几何的意义:反映了两个向量的相似度
- 两个向量的长度与它们夹角余弦的积
- a ⃗ ⋅ b ⃗ = ∣ a ∣ ∣ b ∣ cos ( θ ) {\vec a \cdot \vec b = |a| |b| \cos(\theta)} a⋅b=∣a∣∣b∣cos(θ)
1.1 向量叉乘
- 在数学和向量代数领域,叉积(英语:Cross product)又称向量积(英语:Vector product),是对三维空间中的两个向量的二元运算,使用符号 × {\displaystyle \times } ×。与点积不同,它的运算结果是向量。对于线性无关的两个向量 a {\displaystyle \mathbf {a} } a和 b {\displaystyle \mathbf {b} } b,它们的叉积写作 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } a×b,是 a {\displaystyle \mathbf {a} } a和 b {\displaystyle \mathbf {b} } b所在平面的法线向量,与 a {\displaystyle \mathbf {a} } a和 b {\displaystyle \mathbf {b} } b都垂直。叉积被广泛运用于数学、物理、工程学、计算机科学领域。
- 叉积和点积一样依赖于欧几里德空间的度量,但与点积之不同的是,叉积还依赖于定向或右手定则。
- 两个向量
a
{\displaystyle \mathbf {a} }
a和
b
{\displaystyle \mathbf {b} }
b的叉积仅在三维空间中有定义,写作
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a×b。在物理学中,叉积有时也被写成
a
∧
b
{\displaystyle \mathbf {a}^ \wedge \mathbf {b} }
a∧b,但在数学中
a
∧
b
{\displaystyle \mathbf {a}^ \wedge \mathbf {b} }
a∧b是外代数中的外积。
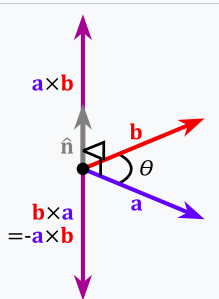
几何意义:
- 叉积 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } a×b是与 a {\displaystyle \mathbf {a} } a和 b {\displaystyle \mathbf {b} } b都垂直的向量 c {\displaystyle \mathbf {c} } c。其方向由右手定则决定,模长等于以两个向量为边的平行四边形的面积。
- 叉积可以定义为:
a × b = ∥ a ∥ ∥ b ∥ sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\ \mathbf {n} } a×b=∥a∥∥b∥sin(θ) n
其中 θ {\displaystyle \theta } θ表示 a {\displaystyle \mathbf {a} } a和 b {\displaystyle \mathbf {b} } b在它们所定义的平面上的夹角( 0 ∘ ≤ θ ≤ 18 0 ∘ {\displaystyle 0^{\circ }\leq \theta \leq 180^{\circ }} 0∘≤θ≤180∘)
三维坐标相乘:
a
×
b
=
(
a
2
b
3
−
a
3
b
2
)
i
+
(
a
3
b
1
−
a
1
b
3
)
j
+
(
a
1
b
2
−
a
2
b
1
)
k
=
∣
i
j
k
a
1
a
2
a
3
b
1
b
2
b
3
∣
{\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} \\&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}\end{aligned}}}
a×b=(a2b3−a3b2)i+(a3b1−a1b3)j+(a1b2−a2b1)k=∣∣∣∣∣∣ia1b1ja2b2ka3b3∣∣∣∣∣∣
叉积表示:
a
×
b
=
a
^
b
=
[
0
−
a
3
a
2
a
3
0
−
a
1
−
a
2
a
1
0
]
a\times b = \hat{a}b = \begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 &0 \end{bmatrix}
a×b=a^b=⎣⎡0a3−a2−a30a1a2−a10⎦⎤
求导:
d
d
t
(
a
×
b
)
=
d
a
d
t
×
b
+
a
×
d
b
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}}}
dtd(a×b)=dtda×b+a×dtdb
1.2 数学推算
- 由上推算可知,叉积表示:
a × b = a ^ b = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] a\times b = \hat{a}b = \begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 &0 \end{bmatrix} a×b=a^b=⎣⎡0a3−a2−a30a1a2−a10⎦⎤ (1-1)
其中 a ^ \hat{a} a^为向量 a a a的反对称矩阵 - 对于,𝑋为三维空间点在世界坐标系下的齐次坐标
X
=
[
x
y
z
1
]
X =\begin{bmatrix} x\\ y\\ z\\ 1\end{bmatrix}
X=⎣⎢⎢⎡xyz1⎦⎥⎥⎤,和
t
=
[
r
1
r
2
r
3
]
=
[
R
t
]
{t=\begin{bmatrix} r_1\\r_2 \\r_3 \end{bmatrix}}=\begin{bmatrix} R & t \end{bmatrix}
t=⎣⎡r1r2r3⎦⎤=[Rt]为世界坐标系到相机坐标系的变换。和
x
=
[
u
v
1
]
x = \begin{bmatrix}u\\ v\\ 1\end{bmatrix}
x=⎣⎡uv1⎦⎤为归一化平面坐标,
λ
{\lambda}
λ为深度值,有:
λ x = T X \lambda x= TX λx=TX => λ x × T X = 0 \lambda x \times TX =0 λx×TX=0 => x ^ T X = 0 \hat{x}TX=0 x^TX=0 (1-2) - 将(1-1)带入(1-2)展开有:
x ^ T X = [ 0 − 1 v 1 0 − u − v u 0 ] [ r 1 r 2 r 3 ] X = [ − r 2 + v r 3 r 1 − u r 3 − v r 1 + u r 2 ] X \hat{x}TX= \begin{bmatrix} 0 & -1 & v\\ 1 & 0 & -u\\ -v & u &0 \end{bmatrix}\begin{bmatrix} r_1\\ r_2\\ r_3 \end{bmatrix}X=\begin{bmatrix} -r_2 +vr_3\\ r_1-ur_3\\ -vr_1+ur_2 \end{bmatrix}X x^TX=⎣⎡01−v−10uv−u0⎦⎤⎣⎡r1r2r3⎦⎤X=⎣⎡−r2+vr3r1−ur3−vr1+ur2⎦⎤X (1-3) - 其中
[
−
r
2
+
v
r
3
r
1
−
u
r
3
−
v
r
1
+
u
r
2
]
\begin{bmatrix} -r_2 +vr_3\\ r_1-ur_3\\ -vr_1+ur_2 \end{bmatrix}
⎣⎡−r2+vr3r1−ur3−vr1+ur2⎦⎤,第一行 叉乘(-u),第二行叉乘(-v),二者相加,可得到第三行,因此,其线性相关,保留前两行即可,有:
[ − r 2 + v r 3 r 1 − u r 3 ] X = 0 \begin{bmatrix}-r_2 +vr_3\\ r_1-ur_3 \end{bmatrix}X=0 [−r2+vr3r1−ur3]X=0 - 因此,已知一个归一化平面坐标
x
x
x和变化
T
c
w
T_{cw}
Tcw,可以构建两个关于X的线性方程组,有两个以上的图像观测,即可求出X:
[ − r 2 ( 1 ) + v r 3 ( 1 ) r 1 ( 1 ) − u r 3 ( 1 ) − r 2 ( 2 ) + v r 3 ( 2 ) r 1 ( 2 ) − u r 3 ( 2 ) ⋮ ] X = 0 \begin{bmatrix}-r_2^{(1)} +vr_3^{(1)}\\ r_1^{(1)}-ur_3^{(1)} \\ -r_2^{(2)} +vr_3^{(2)}\\ r_1^{(2)}-ur_3^{(2)}\\ \vdots\end{bmatrix}X=0 ⎣⎢⎢⎢⎢⎢⎢⎡−r2(1)+vr3(1)r1(1)−ur3(1)−r2(2)+vr3(2)r1(2)−ur3(2)⋮⎦⎥⎥⎥⎥⎥⎥⎤X=0 - 上述方程没有非零解,使用SVD求最小二乘解,解可能不满足齐次坐标形式(第四个元素为1), 齐次坐标 X 即为H的最小奇异值的奇异向量。(SVD好重要–直接线性变换DLT都用到它求解)
因此, X = [ x y z 1 ] = [ x 0 / x 3 x 1 / x 3 x 2 / x 3 x 3 / x 3 ] X = \begin{bmatrix} x \\y\\z\\1\end{bmatrix} = \begin{bmatrix} x_0/x_3 \\x_1/x_3 \\ x_2/x_3\\x_3/x_3\end{bmatrix} X=⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡x0/x3x1/x3x2/x3x3/x3⎦⎥⎥⎤ - 求得空间点坐标,但是这个解几何意义不明确[1],属于代数最小误差解。不等价于最小重投影误差,也不是最小化3D点距离误差。
- 在VINS-Mono中给出了归一化平面坐标
x
=
[
u
v
1
]
x = \begin{bmatrix}u\\ v\\ 1\end{bmatrix}
x=⎣⎡uv1⎦⎤,如果只是给出像素坐标
x
′
=
[
u
′
v
′
1
]
x^{'} = \begin{bmatrix}u^{'} \\ v^{'} \\ 1\end{bmatrix}
x′=⎣⎡u′v′1⎦⎤,并且已知相机内参𝐾,求解3D点坐标方式类似。
λ x ′ = K T X \lambda x{'}= KTX λx′=KTX => λ x ′ × K T X = 0 \lambda x{'} \times KTX =0 λx′×KTX=0 => x ^ ′ K T X = 0 \hat{x}{'} KTX=0 x^′KTX=0 => x ^ ′ P X = 0 \hat{x}{'} PX=0 x^′PX=0
2、代码实现
2.1 VINS-Mono 三角化
//三角化两帧间某个对应特征点的深度
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
Matrix4d design_matrix = Matrix4d::Zero();
design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
Vector4d triangulated_point;
triangulated_point =
design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
point_3d(0) = triangulated_point(0) / triangulated_point(3);
point_3d(1) = triangulated_point(1) / triangulated_point(3);
point_3d(2) = triangulated_point(2) / triangulated_point(3);
}
2.2 orb-slam 三角化
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
cv::Mat A(4,4,CV_32F);
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
cv::Mat u,w,vt;
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
x3D = vt.row(3).t();
cout<<"vt.row()"<<vt.rows<<std::endl;
x3D = x3D.rowRange(0,3)/x3D.at<float>(3);///
}
2.3 Triangulate
void triangulate ( const Eigen::Matrix3d& K,
const Eigen::Matrix4d T1, const Eigen::Matrix4d& T2,
const Eigen::Vector2d& uu1, const Eigen::Vector2d& uu2,
Eigen::Vector4d& X )
{
// construct P1 P2
const Eigen::Matrix<double, 3, 4> P1 = K * T1.block(0,0, 3, 4);
const Eigen::Matrix<double, 3, 4> P2 = K * T2.block(0, 0, 3, 4);
// get vectors
const Eigen::Matrix<double, 1, 4>& P11 = P1.block(0, 0, 1, 4);
const Eigen::Matrix<double, 1, 4>& P12 = P1.block(1, 0, 1, 4);
const Eigen::Matrix<double, 1, 4>& P13 = P1.block(2, 0, 1, 4);
const Eigen::Matrix<double, 1, 4>& P21 = P2.block(0, 0, 1, 4);
const Eigen::Matrix<double, 1, 4>& P22 = P2.block(1, 0, 1, 4);
const Eigen::Matrix<double, 1, 4>& P23 = P2.block(2, 0, 1, 4);
const double& u1 = uu1[0];
const double& v1 = uu1[1];
const double& u2 = uu2[0];
const double& v2 = uu2[1];
// construct H matrix.
Eigen::Matrix4d H;
H.block(0, 0, 1, 4) = v1 * P13 - P12;
H.block(1, 0, 1, 4) = P11 - u1 * P13;
H.block(2, 0, 1, 4) = v2 * P23 - P22;
H.block(3, 0, 1, 4) = P21 - u2 * P23;
// SVD
Eigen::JacobiSVD<Eigen::MatrixXd> svd ( H, Eigen::ComputeFullU | Eigen::ComputeFullV );
Eigen::Matrix4d V = svd.matrixV();
X = V.block(0, 3, 4, 1);
X = X / X(3, 0);
} // triangulate






















 882
882











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








