算法——贪心算法解0-1背包问题

问题的描述

我们先根据一个贪心算法的经典应用实例，然后给出贪心算法的实现步骤与关键环节，最后给出C++代码求解0-1背包问题。

背包问题（Knapsack Problem）：有$N$件物品有一个承重（也可受限于体积）为$C$的背包，每件物品具有二维属性，分别是重量属性$w_i,\quad i=1,\ldots,N$，和价值属性$p_i,\quad i=1,\ldots,N$，求解将哪几件物品装入背包可使这些物品在重量不超过$C$的情况下价值总和最大。背包问题给我们提供了一个模型，由此我们可以求解货箱装载问题。这一问题隐含了一个条件，每个物品只有一件，也就是要么不选取（UNCHOSEN，0），要么选取（CHOSEN，1），因此又称为0-1背包问题。

贪心算法的基本设计思想有以下三个步骤：

1. 建立对问题精确描述的数学模型，包括定义最优解的模型。

   显然本题，就是重量不超过$C$条件下的价值最大

   $$\max W(n)\\ s.t. \sum_iC_i\leq C$$

   1. 将问题分解为一系列子问题，同时定义子问题的最优解结构

      贪心算法的关键环节，将问题分解为后续的一个一个的子问题。本例而言，就是在（根据一定的标准）选定一个物品（重量为$w_i$）的情况下，在余下的物品中选择下一个物品此时的问题的条件是重量不超过$C':=C-w_i$。
      

      $$\max W(n):=w_i+W(n-1)\\ s.t. \sum_{j\setminus i}w_j\leq C-w_i$$

   2. 引用相应的贪心原则（比如重量最轻，价值最高，性价比最高）确定每个子问题的局部最优解（上文所说的$C_i$），并根据最优解的模型，用子问题的局部最优解堆叠出全局最优解。

   下面我们来看这一具体的实例，

   • $C=150$, 最大承重
   • $w_i=[35, 30, 60, 50, 40, 10, 25]$，每个物品的重量
   • $p_i=[10, 40, 30, 50, 35, 40, 10]$，每个物品的价格

   关键在于子问题的定义，本例，我么可以将子问题定义为，在选取某一物品（$w_i$）放入背包以后，在背包容量还有$C':=C-w_i$的情况下，选择下一个物品放入背包。

   如何选择每一次子问题的所需确定的物品呢？这正是贪心策略的选择问题了。对于本题，常见的贪婪策略有三种，

   • 根据物品价值选择，每次都选价值最高的物品

     [4, 2, 6, 5]-> 130（总重量），165（价值）

   • 根据物品重量选择，每次都选最轻的

     [6, 7, 2, 1, 5] -> 140（总重量），155（总价格）

   • 根据价值密度（也即性价比），每次都选性价比最高的

     性价比：[0.286, 1.333, .5, 1., .0875, 4., 1.2]
     [6, 2, 7, 4, 1] -> 150（总重量），170（总价格）

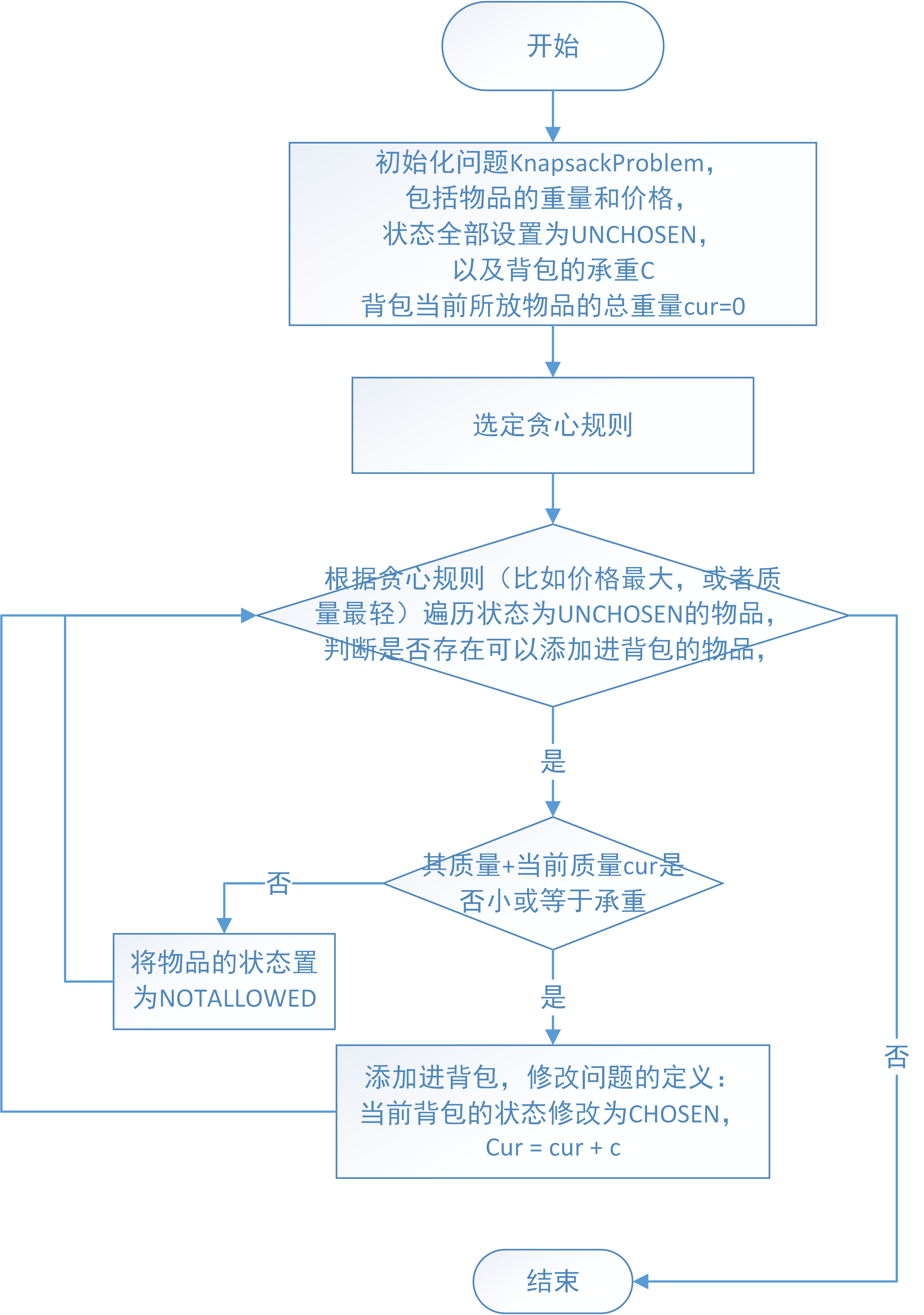
   算法的实现

   算法流程如下：

   • 元素数据结构的定义

   • 问题数据结构的定义

   • 循环子问题，直到全部子问题都得以解决，退出循环

   

   下面给出其实现：

   enum STATUS
   {
       UNCHOSEN,
       CHOSEN,
       NOTALLOWED
   };
   
   // 物品的数据结构定义
   typedef struct tagObject
   {
       int weight;
       int price;
                       // double density; 
                       // 这里也可增加这样一个冗余性定义，用于第三种贪心规则
       STATUS status;
   }OBJ;
   
   // 问题的数据结构定义
   typedef struct tagKnapsackProblem
   {
       std::vector<OBJ> objs;
       int total;
       // std::vector<int> selected;    // 贪心规则下得到的物品
       // int weights;                  // 贪心规则下得到的总的物品重量
       // int prices;                   // 贪心规则下得到的总的物品价格
   }KnapsackProblem;
   
   // 定义三种贪心算法的函数指针
   typedef int(*SELECT_POLICY)(std::vector<OBJ>&);
   
   void greedyAlgo(KnapsackProblem* problem, SELECT_POLICY spFunc)
   {
       int idx;
       int cur = 0;
       while ((idx = spFunc(problem->objs)) != -1)
       {
           // idx标识可选的物品
           if (problem->objs[idx].weight <= problem->total - cur)
           {
               std::cout << idx + 1 << std::endl;
                       // 打印每一个子问题的最优选择
               problem->objs[idx].status = CHOSEN;
               cur += problem->objs[idx].weight;
           }
           else
           {
               problem->objs[idx].status = NOTALLOWED;
           }
       }
   }
   
   int chooseFunc1(std::vector<OBJ>& objs)
   {
       int idx = -1;
       int tmp = 0;
       for (size_t i = 0; i < objs.size(); ++i)
       {
           if (objs[i].status == UNCHOSEN && tmp < objs[i].price)
           {
               tmp = objs[i].price;
               idx = i;
           }
       }
       return idx;
   }
   
   int chooseFunc2(std::vector<OBJ>& objs)
   {
       int idx = -1;
       int tmp = 1000000;
       for(size_t i = 0; i < objs.size(); ++i)
       {
           if (objs[i].status == UNCHOSEN && tmp > objs[i].weight)
           {
               tmp = objs[i].weight;
               idx = i;
           }
       }
       return idx;
   }
   
   int chooseFunc3(std::vector<OBJ>& objs)
   {
       int idx = -1;
       double tmp = 0.;
       for(size_t i = 0; i < objs.size(); ++i)
       {
           if (objs[i].status == UNCHOSEN && 
                   tmp < static_cast<double>(objs[i].price)/objs[i].weight)
           {
               tmp = static_cast<double>(objs[i].price)/objs[i].weight;
               idx = i;
           }
   
       }
       return idx;
   }

   // 客户端代码
   int main(int, char**)
   {
       std::vector<OBJ> objs{{35, 10, UNCHOSEN}, {30, 40, UNCHOSEN}, {60, 30, UNCHOSEN}, {50, 50, UNCHOSEN},   
       {40, 35, UNCHOSEN}, {10, 40, UNCHOSEN}, {25, 10, UNCHOSEN}};
       KnapsackProblem problem = {objs, 150};
       // greedyAlgo(&problem, chooseFunc1);
       // greedyAlgo(&problem, chooseFunc2);
       greedyAlgo(&problem, chooseFunc3);           // 三种贪心规则分别运行。
       return 0;
   }

   0-1找零问题

   有了上述0-1（to be or not to be, 只能二选一）背包问题提供的模型，我们便可比较轻易的仿制上述设计与编程，解决0-1找零钱问题：

   货币$m_i=[25, 10, 5, 1]$分四种，需找给用户41分钱。

   enum STATUS
   {
       CHOSEN,
       UNCHOSEN,
       NOTALLOWED
   };
   typedef struct tagObject
   {
       int value;
       STATUS status;
   }OBJ;
   typedef struct tagProblem
   {
       std::vector<OBJ> objs;
       int total;
   }Problem;
   
   int findMax(std::vector<OBJ>& objs)
   {
       int idx = -1;
       int tmp = 0;
       for (size_t i = 0; i < objs.size(); ++i)
       {
           if (objs[i].status == UNCHOSEN && tmp < objs[i].value)
           {
               idx = i;
               tmp = objs[i].value;
           }
       }
       return idx;
   }
   
   void greedyAlgo(Problem* prob)
   {
       int idx;
       int cur = 0;
       while ((idx = findMax(prob->objs))!=-1)
       {
           if (prob->objs[idx].value <= prob->total - cur)
           {
               std::cout << idx + 1 << std::endl;
               prob->objs[idx].status = CHOSEN;
               cur += prob->objs[idx].value;
           }
           else
           {
               prob->objs[idx].status = NOTALLOWED;
           }
       }
   }
   
   int main(int, char**)
   {
       std::vector<OBJ> objs {{25, UNCHOSEN}, {10, UNCHOSEN}, {5, UNCHOSEN}, {1, UNCHOSEN}};
       Problem prob = {objs, 41};
       greedyAlgo(&prob);
       return 0;
   }