【智能算法】鸡群优化算法（CSO）原理及实现

---

1.背景

2014年，X Meng等人受到鸡群社会行为启发，提出了鸡群优化算法（Chicken Swarm Optimization, CSO）。

2.算法原理

2.1算法思想

CSO算法的思想是基于对鸡群的模拟行为，其中鸡的身份（公鸡、母鸡和小鸡）取决于其适应度值。适应度值最好的鸡被选为公鸡，适应度值最差的鸡被认为是小鸡，其余鸡被视为母鸡。鸡群中的等级秩序、优势关系和母子关系定期更新。公鸡带领同伴寻找食物，但也会阻止其他鸡吃掉它们的食物。

2.2算法过程

适合度值高的公鸡比适合度值低的公鸡优先获得食物，适合度值越高的攻击搜索范围越大：
$$\begin{gathered} x_{i,j}^{t+1}=x_{i,j}^t\ast (1+Randn(0,{\sigma }^2)). \\ {\sigma }^2=\{\begin{array}{l}1,if{f}_i\le f_k,\\ \exp (\frac{(f_k-f_i)}{|f_i|+\epsilon }),otherwise,\end{array}k\in [1,N],k\ne i.\text{\hspace{1em}(1)} \end{gathered}$$
母鸡跟随公鸡一起寻找食物，也会随机偷取其他鸡找到的好食物，尽管受到其他鸡的抑制。在食物争夺中，强势的母鸡比温顺的母鸡更具优势：
$$\begin{gathered} x_{i,j}^{t+1}=x_{i,j}^t+S1\ast Rand\ast \left(x_{r1,j}^t-x_{i,j}^t\right)+S2\ast Rand\ast \left(x_{r2,j}^t-x_{i,j}^t\right) \\ S1=\exp ((f_i-f_{r1})/(abs(f_i)+\epsilon )) \\ S2=\exp ((f_{r2}-f_i))\text{\hspace{1em}(2)} \end{gathered}$$
母鸡的适应度值越小，S1越接近1，与公鸡的位置差距越小，统治力更强的母鸡更有可能吃到食物，小鸡在母亲周围寻找食物：
$$x_{i,j}^{t+1}=x_{i,j}^t+FL\ast (x_{m,j}^t-x_{i,j}^t)\text{\hspace{1em}(3)}$$

伪代码

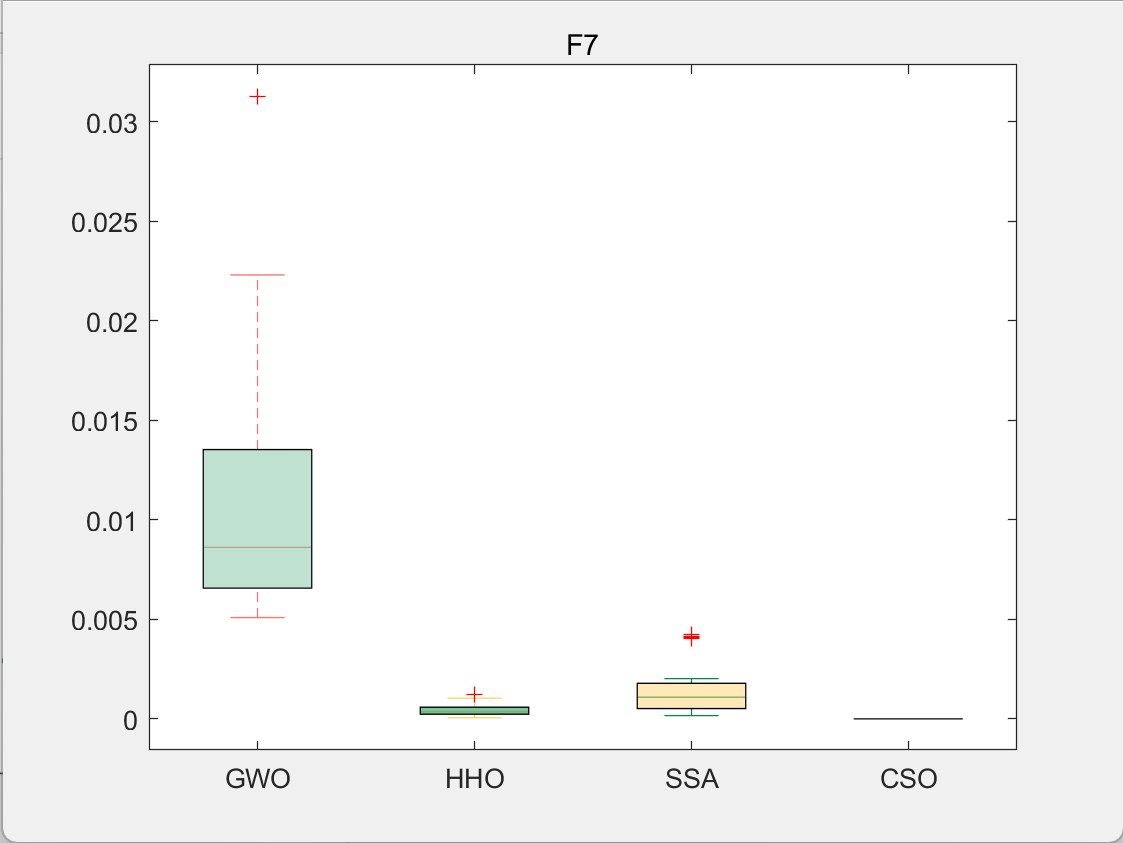
3.结果展示

4.参考文献

[1] Meng X, Liu Y, Gao X, et al. A new bio-inspired algorithm: chicken swarm optimization[C]//Advances in Swarm Intelligence: 5th International Conference, ICSI 2014, Hefei, China, October 17-20, 2014, Proceedings, Part I 5. Springer International Publishing, 2014: 86-94.