阴阳对优化算法：一种新颖的轻量级优化算法

---

1.摘要

本文提出了一种新的优化算法——阴阳对优化算法（YYPO），其核心在于平衡搜索空间的探索与利用。该算法具有低复杂度和高灵活性，用户可以通过定义三个参数来调节其搜索行为，以适应不同的优化需求。

2.算法原理

阴阳对优化算法（YYPO）汲取了宇宙中普遍存在的二元性原理，例如光与暗、身与心、男与女、生与死等，以及科学领域中的波粒关系、正负电荷等二元对立现象。这些对立在中国哲学中被阐释为阴阳，两个互补且相互依存的极端，通过不断的转换与循环相互作用，实现整体的和谐。在进化计算领域，算法的效能取决于开发和探索这两种相互冲突的行为之间的平衡。

YYPO算法将所有决策变量归一化到[0,1]，使用两个核心点P1和P2来分别来进行开发和探索阶段。算法中的两个点探索由各自的半径${\delta }_1$和${\delta }_2$定义的超球体体积，其中${\delta }_1$倾向于减小而${\delta }_2$倾向于增大。算法由分裂阶段和归档阶段组成，通过不断的迭代，两点及其半径值会根据适应度进行调整和更新。算法开始时随机生成两个点，并在迭代过程中评估和调整这些点的适应度，以维持其性能的最优化。

分裂阶段

在阴阳对优化算法的分裂阶段，输入包括选定的一个点（P1或P2）及其对应的搜索半径（${\delta }_1$和${\delta }_2$）。虽然两个点都参与分裂阶段，但一次只有一个点P及其搜索半径$\delta$实际进行分裂。分裂阶段旨在在保持随机性的同时，尽可能在多个方向上围绕点P和其半径$\delta$生成新点。单向分裂：
$$\begin{array}{rl}& S_j^j=S^j+r\delta \\ & S_{D+j}^j=S^j-r\delta \end{array}$$

D-way分裂：
$$\begin{array}{rl}{S}_k^j& =S^j+r\left(\delta /\sqrt{2}\right)\mathrm{if}{B}_k^j\\ & =1,S_k^j=S^j-r\left(\delta /\sqrt{2}\right)\mathrm{else},\mathrm{where}k=1,2,3\dots 2D\\ & andj=1,2,\mathrm{3...}D\end{array}$$

归档阶段

归档阶段在达到预定的归档更新次数后开始，此阶段的归档包含$2I$个点，这些点来源于每次更新前分裂阶段所添加的两个点P1和P2。在这个阶段，如果归档中的某个点比点P1更适合，这个点将与P1交换位置。如果归档中存在比点P2更适合的点，该点则会替换P2。此外，即使点P1已经与归档中的点交换，之前已加入归档的点仍可能被用来替换点P2。归档阶段通过这种方式保持了算法的精英性，并确保了算法的单调收敛性，即在任何迭代过程中确定的最佳点不会丢失。这一阶段后续还将通过特定方程更新搜索半径${\delta }_1$和${\delta }_2$，以优化后续的搜索过程：
$$\begin{array}{rl}{\delta }_1& ={\delta }_1-({\delta }_1/\alpha )\\ {\delta }_2& ={\delta }_2+({\delta }_2/\alpha )\end{array}$$

伪代码

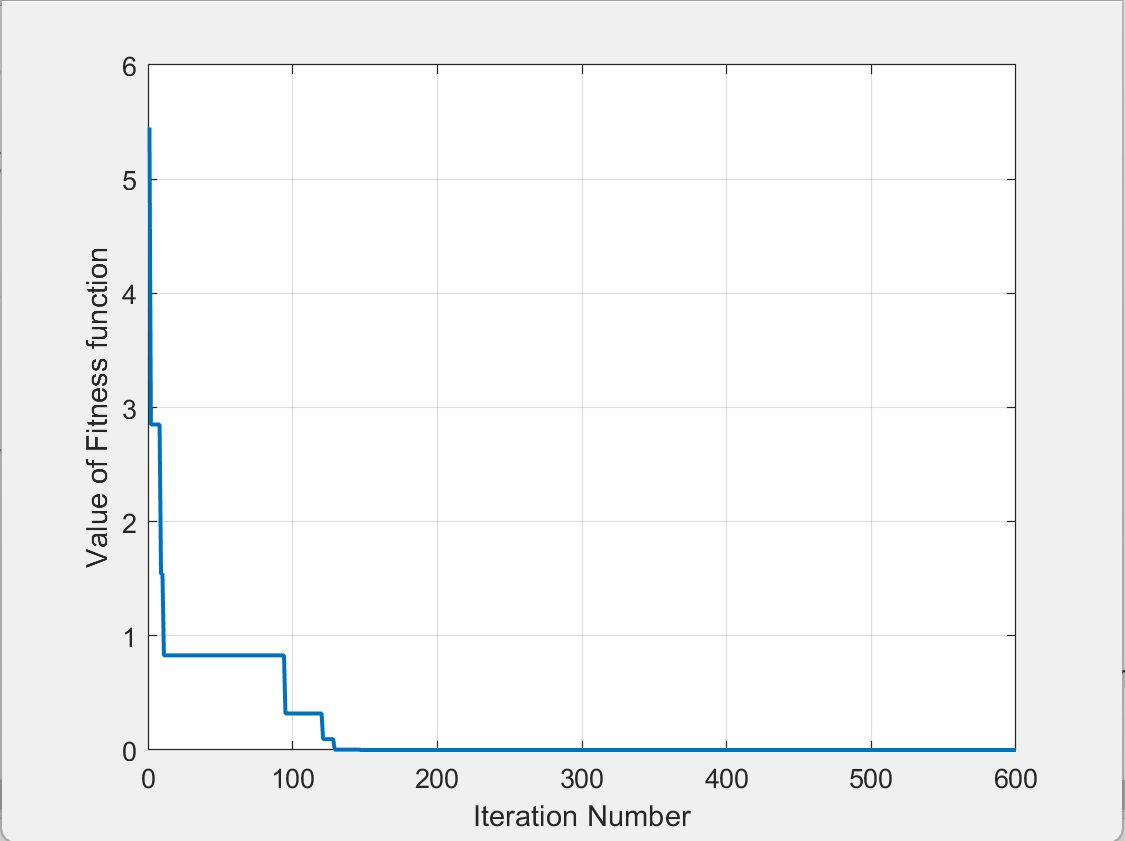
3.结果展示

Rastrigin函数

4.参考文献

[1] Punnathanam V, Kotecha P. Yin-Yang-pair Optimization: A novel lightweight optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2016, 54: 62-79.

5.代码获取