2025年群智能SCI1区：非线性降维搜索差分进化算法NDRDE，深度解析+性能实测-CSDN博客

本文链接：https://blog.csdn.net/Logic_9527/article/details/145736219

1.摘要

大规模优化问题由于搜索空间的高维性和所需的大量计算资源，面临着显著的挑战。因此，本文提出了一种新型算法——非线性降维搜索差分进化算法（NDRDE），该算法通过将非线性降维技术与差分进化算法相结合，用于有效应对大规模优化中的高维和计算资源消耗问题。

NDRDE的核心创新在于其随机降维策略，这种策略不仅增强了种群的多样性，还提高了算法的探索能力。此外，NDRDE采用了一种球形搜索方法，能够最大限度地消除方向信息，从而增加搜索的随机性，改善探索阶段的效率。

2.差分进化算法DE原理

在过去几十年中，差分进化（DE）算法逐渐成为一种在连续优化任务中非常有前景的算法。L-SHADE是最成功的变种之一，L-SHADE的迭代过程包括变异、交叉和选择，其中选择操作使用贪婪策略来保留新的个体。此外，L-SHADE还具备种群规模线性减少的特性。L-SHADE变异算子：
$P_{i,j}=X_{i,j}+F\cdot \begin{pmatrix} X_{best,j}-X_{i,j}+X_{r1,j}-X_{r2,j} \end{pmatrix}$

交叉算子：
$U_{i,j}= \begin{cases} P_{i,j}, & \mathrm{if}rand<CR_i \\ X_{i,j}, & \mathrm{otherwise} & \end{cases}$

其中， $CR, F$ 初始值设置为0.5，在每次迭代中自适应更新：
$\begin{aligned} & F_{i}=C(M_{F,r},0.1) \\ & C_{Ri}=\mathcal{N}(M_{C,r},0.1) \end{aligned}$

其中， $C,\mathcal{N}$ 分别表示柯西分布和正态分布。 $M_{F,r}$ 和 $M_{C,r}$ 是从外部档案中随机选取的均值，这些外部档案通过贪婪策略保留上一代中个体的 $C_{R}$ 和 $F$ 值生成。

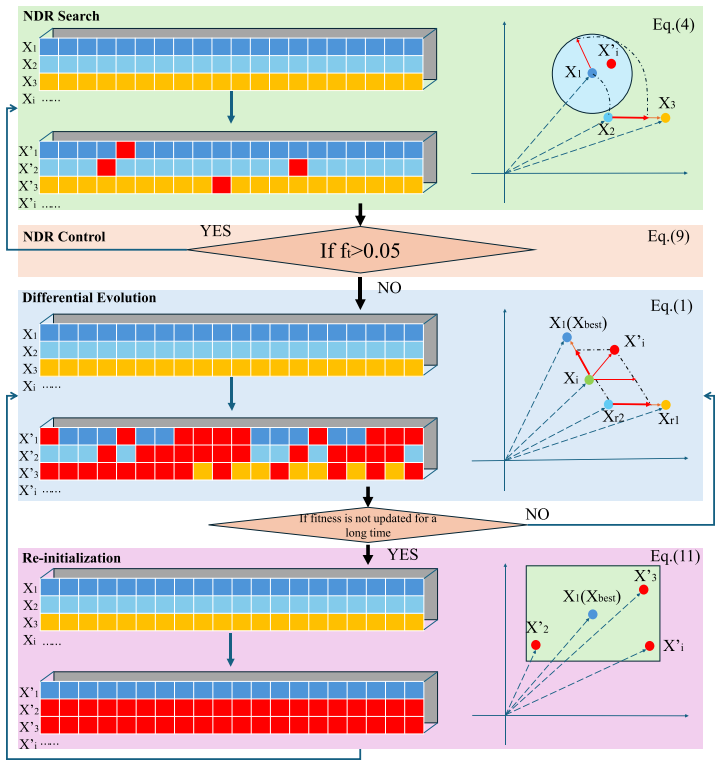
3.改进策略

非线性降维搜索

在NDRDE的探索阶段（NDR搜索）中，多个维度会被随机选择进行更新。NDR搜索的主要目标是在有限的评估次数内最大化搜索效果，确保搜索范围具有价值。
每个个体在NDR中的每个维度的迭代过程可表示为：
$X_{i,j}^{\prime}= \begin{cases} X_{i,j}+S_{i,j}, & \mathrm{if}j\in D_i \\ X_{i,j}, & \mathrm{otherwise} & \end{cases}$

其中， $n$ 在开始时被随机初始化为1或2，每个个体的 $n$ 更新：
$\begin{cases} n, & \mathrm{if}fit^{t+1}<fit^t \\ n+\lceil rand(0,2)\rceil, & \mathrm{elseif}n\cdot rand<n_p \\ n-\lceil rand(0,2)\rceil, & \mathrm{otherwise} & \end{cases}$

球面搜索可以通过将多维信息转化为低维向量来表示多维信息:
$\begin{aligned} & S_{i,j}=D_{j}\cdot\cos\theta \\ & S_{i,j}\left.= \begin{cases} D_{j}\cdot\sin\theta, & \mathrm{if}j=d_{i,1} \\ D_{j}\cdot\cos\theta, & \mathrm{if}j=d_{i,2} & \end{cases}\right. \\ & S_{i,j}= \begin{cases} \mathcal{D}_{j}\cdot\prod_{j}^{D-1}\cdot\sin\theta_{j}, & \mathrm{if}j=d_{i,1} \\ \mathcal{D}_{j}\cdot\cos\theta_{j-1}, & \mathrm{if}j=d_{i,n} \\ \mathcal{D}_{j}\cdot\prod_{j}^{D-1}\cdot\cos\theta_{j-1}\cdot\sin\theta_{j}, & \mathrm{otherwise} & \end{cases} \end{aligned}$
其中， $D_j$ 表示 $X_{r_1,j} - X_{r_2,j} \|$ ， $\theta$ 是用于获取球形搜索中所需随机方向的随机角度。NDRDE的降维策略是随机的，能够增强种群多样性，并使得在黑箱问题中更容易找到全局最优解。球形搜索方法最大程度地消除方向信息，增加随机性并提高探索能力。将NDR与球形搜索结合，极大地增强了算法的探索能力。

NDR控制设计

为了获得最佳优化结果，降维后的局部搜索至关重要，它能够恢复高密度的交互信息。NDRDE采用投票机制来决定搜索模式，当NDR搜索的进展速率超过预设的阈值时，迭代次数会增加；否则，搜索过程将结束。局部搜索需要更多的迭代来实现高精度的开发。在大规模全局优化（LSGO）问题中，由于评估次数有限，策略切换条件较为严格。NDR的性能每完成总迭代的0.5%时进行评估，如果未达到设定的阈值，算法将切换为L-SHADE搜索。为此，NDRDE采用了一种线性投票机制来决定何时进行切换：
$V_t= \begin{cases} V_t+O_t, & \mathrm{if}f_t>0.05 \\ 0, & \mathrm{otherwise} & \end{cases}$

其中， $V_t$ 是预设评估次数， $O_t$ 是合同续签次数， $f_t$ 是在预设评估次数下的适应度进展程度：
$f_t=1-\frac{fit_{min}}{fit_{old}}$

重新初始化

重新初始化是一种常用的技术，旨在克服局部最优解的问题，并已被广泛应用于许多研究中。NDRDE通过提出多个以已知信息为中心的小搜索范围，来缩小搜索空间。在这些范围之外的个体将被重新初始化，并限制在小范围内进行搜索。算法将局部搜索空间划分为多个区域，并以适应度排名最高的个体为中心进行探索。对于缺失的个体，它们将通过随机初始化并围绕这些中心个体进行重置：
$X_{i,j}^{\prime}= \begin{cases} X_{g,j}, & \mathrm{if~}i\leq h \\ X_{g,j}+c & \mathrm{if~}h<i\leq q \\ X_{g,j}+k & \mathrm{otherwise} & \end{cases}$

伪代码

在这里插入图片描述
流程图

在这里插入图片描述

4.结果展示

在这里插入图片描述

5.参考文献

[1] Yang Y, Li H, Lei Z, et al. A Nonlinear Dimensionality Reduction Search Improved Differential Evolution for large-scale optimization[J]. Swarm and Evolutionary Computation, 2025, 92: 101832.