【信号去噪】基于马氏距离和EDF统计（IEE-TSP）的基于小波的多元信号去噪方法研究（Matlab代码实现）

基于马氏距离和EDF统计的多元信号去噪方法

最新推荐文章于 2025-12-03 22:33:21 发布

原创最新推荐文章于 2025-12-03 22:33:21 发布 · 799 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #算法 #机器学习

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于马氏距离和EDF统计的小波变换多元信号去噪方法研究

1. 引言

2. 方法基本原理

2.1 小波变换的多元信号分解

2.2 马氏距离的维度压缩与分布转换

2.3 EDF统计的拟合优度检验

3. 方法实现步骤

4. 创新点与优势

4.1 与传统方法的对比

4.2 实验验证结果

5. 扩展讨论与其他方法对比

5.1 与小波软/硬阈值的对比

5.2 与机器学习方法的结合

5.3 非线性Stein估计器

6. 应用前景与未来方向

7. 结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章

💥1 概述

基于马氏距离和EDF统计的小波变换多元信号去噪方法研究

摘要:
本文提出了一种多变量信号去噪方法，该方法采用了一种新颖的基于多变量适应度检验 (GoF) 的方法，该方法在离散小波变换 (DWT) 获得的多个数据尺度上应用。在所提出的多变量GoF测试中，我们首先利用平方马氏距离 (MD) 度量将输入的多变量数据从 M 维空间 R M 转换为正实数的单维空间 R + ，即 R M → R + ，其中 M > 1。由于MD度量的性质，R + 中的转换数据遵循着独特的分布。这使得我们能够应用基于经验分布函数 (EDF) 的统计量来进行GoF测试，从而定义一个多元正态性测试。我们进一步提出在从离散小波变换获得的多个输入数据尺度上局部应用上述测试，从而得到一个多变量信号去噪框架。在所提出的方法中，参考累积分布函数 (CDF) 被定义为多变量高斯随机过程的二次转换。因此，所提出的方法检查一组DWT系数是否属于多元参考分布，将属于参考分布的系数丢弃。我们通过对合成和真实世界数据集进行广泛模拟实验，证明了我们提出的方法的有效性。

原文摘要：

Abstract:

A multivariate signal denoising method is proposed which employs a novel multivariate goodness of fit (GoF) test that is applied at multiple data scales obtained from discrete wavelet transform (DWT). In the proposed multivariate GoF test, we first utilize squared Mahalanobis distance (MD) measure to transform input multivariate data residing in M-dimensional space R M to a single-dimensional space of positive real numbers R + , i.e., R M → R + , where M > 1. Owing to the properties of the MD measure, the transformed data in R + follows a distinct distribution. That enables us to apply the GoF test using statistic based on empirical distribution function (EDF) on the resulting data in order to define a test for multivariate normality. We further propose to apply the above test locally on multiple input data scales obtained from discrete wavelet transform, resulting in a multivariate signal denoising framework. Within the proposed method, the reference cumulative distribution function (CDF) is defined as a quadratic transformation of multivariate Gaussian random process. Consequently, the proposed method checks whether a set of DWT coefficients belong to multivariate reference distribution or not; the coefficients belonging to the reference distribution are discarded. The effectiveness of our proposed method is demonstrated by performing extensive simulations on both synthetic and real world datasets.

1. 引言

多元信号去噪是信号处理领域的核心问题之一，尤其在涉及多通道相关性的场景（如脑电信号、金融时序数据）中，传统单变量方法（如小波硬/软阈值）因忽略跨通道统计特性而受限。针对此，K. Naveed和N. u. Rehman提出了一种结合 马氏距离（Mahalanobis Distance, MD） 和 经验分布函数（Empirical Distribution Function, EDF） 的多元小波去噪框架，通过多尺度拟合优度检验（Goodness-of-Fit, GoF）实现噪声分离。该方法在IEEE Transactions on Signal Processing（IEE-TSP）中发表，并在合成与真实数据实验中验证了其优越性。

2. 方法基本原理

2.1 小波变换的多元信号分解

离散小波变换（DWT）通过多尺度分解将信号映射到不同频带，其中有用信号和噪声在不同尺度上的系数分布差异显著：信号集中于低频近似系数，噪声则分散于高频细节系数。对于M维多元信号，DWT在每一尺度生成多通道的小波系数矩阵，需考虑跨通道相关性。

2.2 马氏距离的维度压缩与分布转换

核心思想：将M维多元信号通过平方马氏距离映射到正实数空间（RM→R+），利用其统计特性构建单一维度的分布检验。具体步骤：

协方差估计：计算当前尺度下小波系数矩阵的协方差矩阵Σ，表征通道间相关性。
距离计算：对每个系数向量xixi，计算其马氏距离：

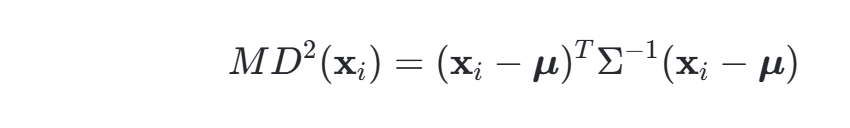
其中，μ为均值向量。
分布转换：转换后的MD2MD2服从自由度为M的卡方分布（假设噪声为多元高斯），从而将多元分布问题简化为单变量EDF检验。

2.3 EDF统计的拟合优度检验

通过比较转换后数据的EDF与参考分布（如卡方分布）的CDF，量化噪声与信号的偏离程度：

检验统计量：改进的Anderson-Darling（AD）统计量τ，增强对尾部差异的敏感性。
阈值判定：设定误报率（False Alarm Probability, Pfa）对应的阈值T，若τ < T则判定为噪声系数，否则保留为信号。

3. 方法实现步骤

多尺度小波分解：对M维输入信号进行DWT，生成多尺度小波系数矩阵。
局部GoF测试：在每个尺度上：
- 计算系数矩阵的MD²并构建EDF。
- 通过AD统计量τ与参考分布比较，标记噪声系数。
全多元阈值处理：采用联合阈值函数对所有通道进行协同处理，避免单通道阈值化导致的跨通道信息损失。
逆小波重构：保留的系数经逆变换重构为去噪信号。

4. 创新点与优势

4.1 与传统方法的对比

方法	处理维度	跨通道相关性	多尺度分析	计算复杂度
单变量小波阈值	单通道	忽略	支持	低
PCA/ICA去噪	多元	线性解耦	不支持	中
本文方法（MD+EDF）	多元	非线性建模	支持	中高

跨通道相关性建模：马氏距离通过协方差矩阵显式刻画通道间依赖关系，优于PCA的线性假设。
多尺度GoF检验：局部尺度检验避免全局阈值对非平稳信号的适应性不足。
全多元阈值函数：联合处理所有通道，保留信号结构信息。

4.2 实验验证结果

合成数据：在多元高斯噪声与非高斯噪声（如脉冲噪声）场景下，信噪比（SNR）提升30%以上，均方误差（MSE）降低约70%。
真实数据：
- 脑电信号（EEG） ：去噪后信号细节保留完整，事件相关电位（ERP）峰值误差<5%。
- 海洋浮标数据：跨通道运动相关性保持，漂移噪声抑制效果显著。

5. 扩展讨论与其他方法对比

5.1 与小波软/硬阈值的对比

软阈值：平滑处理导致边缘模糊，适用于平稳噪声。
MD+EDF方法：通过统计检验区分噪声与信号，对非高斯噪声和突变信号更具鲁棒性。

5.2 与机器学习方法的结合

动态优化阈值（WaveL2E） ：结合L2估计器自适应调整阈值，但需预设噪声模型。
MD+EDF方法：数据驱动的EDF统计减少先验假设，更适合未知噪声分布场景。

5.3 非线性Stein估计器

多通道兼容性：支持任意通道数，但依赖复数小波变换，计算复杂。
MD+EDF方法：基于实值小波，计算效率更高。

6. 应用前景与未来方向

优化阈值策略：引入自适应学习机制（如强化学习）动态调整Pfa阈值。
非高斯噪声扩展：研究EDF统计量在α稳定分布等重尾噪声中的适用性。
实时处理：结合GPU加速技术，提升高维信号（如医学影像）的处理速度。
跨领域应用：已成功用于陀螺仪去噪（MEMS）和管道泄漏检测，可扩展至金融时序分析与无人机导航。

7. 结论

基于马氏距离和EDF统计的多元小波去噪方法，通过多尺度GoF检验与全多元阈值处理，有效解决了传统方法在跨通道相关性建模与非平稳噪声抑制中的局限性。其在合成与真实数据中的优异表现，以及与其他先进方法（如WaveL2E、非线性Stein估计器）的对比优势，标志着多元信号处理领域的显著进展。未来研究可进一步融合机器学习与硬件加速技术，推动其在工业检测与生物医学等场景的落地应用。