反对称阵及其矩阵指数函数

通过对比可以发现,2.1.1式和2.1.2式是相等的,也就是说
若定义下式为反对称阵(或称为斜对称阵,Skew-symmetric matrix),那么就有

两个向量的内积可以写成矩阵相乘的形式,即
![]()
如果V为是实向量(对应实数),那么也有
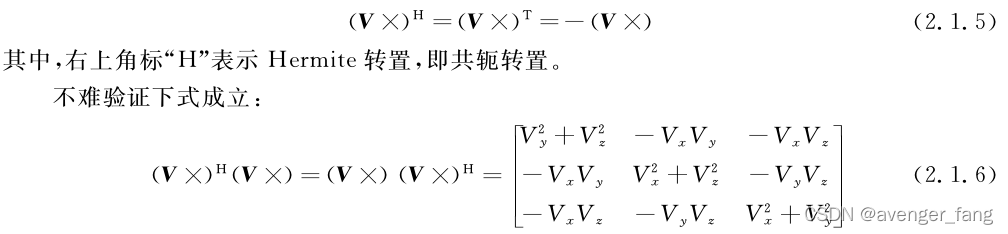
因此,反对称阵是正规矩阵(Normal matrix),任意正规矩阵都可在经过一个酉变换后变为对角矩阵,也就是可以酉相似于对角阵,且不同的特征值对应的特征向量两两正交。
这里,计算反对称阵的特征值与特征向量

将三个特征向量组成一个矩阵U,那么可以发现,
,因此U为酉矩阵。
若记 根据特征值和特征向量的关系,有:
,从而可以知道:
,这也证明了反对称阵
酉相似于对角阵,所对应的酉相似变换矩阵就是U矩阵。
接下来就能得到反对称阵的幂次方公式

其中,即向量V的模长
反对称阵的矩阵函数
根据哈密顿-凯莱定理,矩阵指数函数必定可以展开为矩阵的有限项级数的形式。

其中,
,
为待求系数


 得到结论为:
得到结论为:
 根据式(2.1.16)可以发现有等式成立:
根据式(2.1.16)可以发现有等式成立:
因此
根据特征值与特征向量关系 ,由此可知,
与反对称阵
具有相同的特征向量,它们均为矩阵U的列向量,且矩阵函数
与对角阵
有相同的特征值
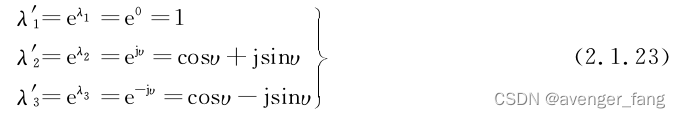
根据以上特征值,易知,因此对角阵
也是酉矩阵,由于多个酉矩阵的乘积仍然为酉矩阵,因此
也是一个酉矩阵,根据式(2.1.20)可知,若V为实向量,那么矩阵函数
必定也是实矩阵,所以矩阵函数
必定是单位正交阵。
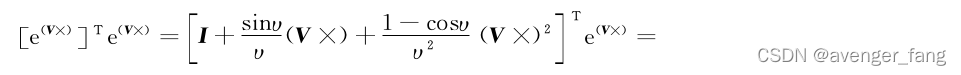
 由于
由于,在所有三阶单位正交阵中只有行列式为1的才能表示为 矩阵函数
的形式。行列式为1的单位正交阵称为右手直角坐标系变换矩阵,行列式为-1的可以称为左手矩阵。
方向余弦和等效旋转矢量
两个直角坐标系之间的旋转变换关系可用方向余弦阵描述,欧拉转到定理表明,刚体从一个角位置到另一个角位置的任意转动总能够等效与绕某一固定轴的一次转动,实际上这一固定轴与转角就构成了等效旋转矢量的概念。

那么会有:

矩阵表示从坐标系i到坐标系b的坐标系变换矩阵,不难验证坐标系变换矩阵P是一个正交矩阵
即,P中任一行为单位向量,不同行向量正交,内积为0。
矩阵的每一行代表i系坐标轴在b系中的余弦值。
姿态更新的四元数表示
四元数顾名思义就是含有四个元的数,它表示为
![]()
其中 均为实数,
为实部,
为虚部。

一个三维矢量可以看成是四一个零标量的四元数。两个四元数相等等价于四个元分别对应相等。

若采用三维矢量运算表示法,表示四元数的乘法,

由于矢量叉乘不满足交换律,因此四元数乘法也不满足交换律,当且仅当四元数虚部矢量相互平行时(包含0矢量)时才满足交换律。四元数乘法满足结合律。乘法对加法满足分配律。
若采用矩阵形式来表示四元数乘法,则有:

四元数的共轭(转置)表示为
![]()
两个四元数的和与积的共轭分别满足如下规则

四元数的模值即(2范数)可以表示为下,代表四元数在四维空间的长度
 因此对于模长不为0的四元数,其有
因此对于模长不为0的四元数,其有

因此可以知道四元数Q的逆为

非零四元数的乘积的逆满足矩阵乘积的逆,即
![]()
四元数的模长不为0,那么就可以实现对四元数的规范化,规范化后四元数的模长为1。显然,单位四元数的共轭与其逆相等,即
![]()
两个单位四元数的乘积也为单位四元数
![]()
对于单位四元数,可以表示为三角函数形式


物理意义:为动坐标系相对于参考坐标系旋转的单位转轴,
表示相对旋转轴的转角大小,
表示等效旋转矢量。

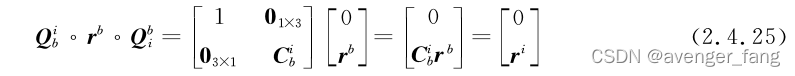 也对应是一个零标四元数,其虚部对应于方向余弦阵的坐标变换
也对应是一个零标四元数,其虚部对应于方向余弦阵的坐标变换
,因此为了书写简洁,定义四元数和三维向量的运算


方向余弦更新算式和四元数更新算式都是假设在更新周期内动坐标系做定轴转动才能严格成立。
参考文献:严恭敏 翁浚《捷联惯导算法与组合导航原理》西北工业大学







 本文探讨了反对称阵的性质,包括其与正规矩阵的关系,以及如何通过酉变换变为对角阵。介绍了矩阵指数函数的展开式,并展示了反对称阵的幂次方公式。此外,还讨论了方向余弦、四元数在姿态更新中的作用,以及四元数乘法的非交换性和几何意义。这些概念在坐标变换和刚体旋转中有重要应用。
本文探讨了反对称阵的性质,包括其与正规矩阵的关系,以及如何通过酉变换变为对角阵。介绍了矩阵指数函数的展开式,并展示了反对称阵的幂次方公式。此外,还讨论了方向余弦、四元数在姿态更新中的作用,以及四元数乘法的非交换性和几何意义。这些概念在坐标变换和刚体旋转中有重要应用。

















 280
280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








