【射影几何02】拓广平面

目录

一、说明

二、拓广直线

三、拓广平面

3.1 几个术语和概念

3.2 关于拓广平面

3.3 拓广平面的实际意义

四、结论

---

一、说明

        随计算机图像、图形学的深入开展。关于几何方面的理论越来越受到重视，其中包括：射影几何、共形几何、微分几何等观点。本篇将系列开展射影几何的概念，以及实时的程序实验。为读者快速打开理论实践结合的大门，保障理论水平的提高。

二、拓广直线

        对于平面上的一条直线来说，如果将正反方向无穷远，并认为无穷远点只有一个，于是无穷远的可以合并，就产生一个类似环状的拓广直线。

图1 拓广直线

• 拓广直线上一点不能把拓广直线分成不连通的两段;而拓广直线上的两普通点把它分成两段,其中一段包含无穷远点,另一段就是原来直线上的线段. 

        拓广直线的启发来源于地球经线总是相交于两级，因此，在陆地上作的平行经线，总是要相交于北极：

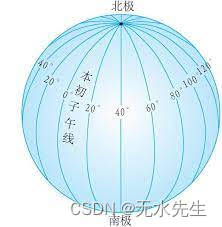
无穷远直线。继续看：

•  L1平行于L2，在无穷远点S1上相汇。 L3平行于L4，在无穷远点S2上相汇。
• L1，L2相交于L3，L4，因而无穷远处的S1和S2也不是同一个点，S1和S2构成无穷远直线。
• 由于L1和L3相交，相交的线能构成平面，因此，无穷多的S1，S2，...S∞构成无穷远封闭盘。包围这个平面。

三、拓广平面

3.1 几个术语和概念

术语	意义	备注
欧氏点	有限空间内点
无穷远点	每条直线的无限远处的抽象点
射影点	欧氏点 +  无穷远点
欧氏直线	有限空间直线，不包含无穷远点
射影直线	欧氏直线+无穷远点的总称。、还有，无穷远点的连线是
欧氏平面	有限欧氏空间的平面。
射影平面	欧氏平面+无限远射影线构成。

为了区分无穷和有限范围，有必要引入一些概念：

1）欧氏点：指的是有限空间内的点，注意，不能与欧氏坐标混淆，欧氏坐标是无限的，但是，能在这个坐标框架下表示的点为A（100，1000）而不能是A（∞，1000）

2）无限远点：注意这个概念，不是说某个点A（∞，1000）或B（∞，∞）；以上A或B没有研究价值。正确的思路是，指极坐标上某一方向下的无穷远点，如下图：

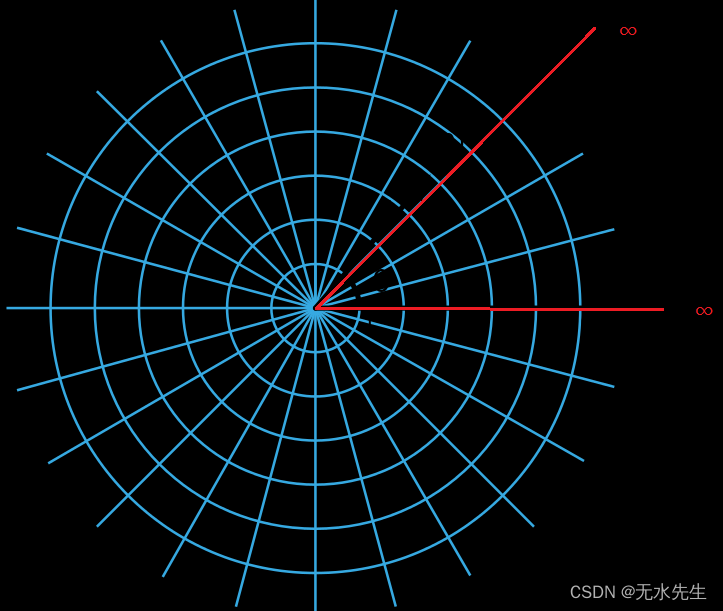
3）射影点：射影点就是视点，就是观察客观事物的视线发出的起点；注意，这个点可以是欧氏点也可以是无穷远点；从欧氏点发出的射影是透视射影；从无穷远点发出的射影是仿射射影（保平行射影）。

4）欧氏直线：在欧氏空间定义的直线，其特点是有限范围的直线，虽然说“直线可以延长到无限”，但从不研究无穷远点的情况。

5）射影直线：射影直线包括欧氏直线和无穷远点连成的直线，注意，无穷远点连成直线如下图：

        假如ABC都是无穷远点，无穷远点AB~连接直线线不是AB连成的直径（AB直径实际上是欧氏直线），而是AB在无穷远圆弧上，经AB过无穷远C点的连结弧，将圆无限扩大的结果，很抽象。

6）欧氏平面：是在欧氏空间的有限平面；

7）射影平面：要么是欧氏平面，要么是欧氏平面+无限远射影线构成。解释如下图：

当球直径无限扩大后，球上每一格看成是欧氏平面，无限延长后，该平面在无限远是连接的。

3.2 关于拓广平面

        拓广平面就是射影平面。

        凡是两个平行的拓展平面都在无穷远处相交，相交于无穷远封闭线。单个拓广平面总时存在。

图2    拓广平行平面 

        图 2 设有平面Ps和Pr平行，则Ps和Pr在无限远处相交，相交的集合是一个无限大半径的园（按照极限论，无限大半径的园，就是直线）。所以，图中和代表无限远圆上的一个点。故：

• 定理1.1.1 拓广平面上任意两点决定一条直线

是这样的事实：

1. 平面上普通两点连成直线。
2. 平面上任意一个点，与无穷远点连成直线。
3. 两个无穷远点连成直线。

                                                                             

        这里提醒的是，“两个无穷远点连成直线” 不是图1中图中和连成直线，事实上，图中和是一个点。“一组平行线在无穷远处交于一个点”，这点务必注意。

        上面说的“ 3）两个无穷远点连成直线” 指的情况如图2所示。

 图三  拓广平面上两组平行线，分别相交于无限远圆的两点上（ c和d ）

                                                                         

        如图三，K1、K2、K3 构成平行线，它们将交于Cu和Cv（两点重合），而无穷远点（Cu和Cv）和无穷远点（du和dv）构成无穷远直线。

• (ⅰ)拓广平面上任意两条拓广直线如果作为普通直线平行,那么此两拓广直线上的无穷远点相同,否则不同;
• (ⅱ)拓广平面上所有的无穷远点构成一条直线,它上面没有普通点,这条直线称为无穷远直线.

3.3 拓广平面的实际意义

        将图四中左边的棋盘格放于地面，然后绘制成拓广平面，如右侧。显然棋盘格上有两组互相垂直的平行线族；分别交于天际线的R点和S点，R和S是无限远的圆上，也就是说，RS这两个无限远点连成一条线。

图四：棋盘在投影后图形样貌，右上图没考虑交比，右下图考虑交比

                                                                       

        右图中上边的目测起来似乎不是平面，而下边的目测更像是个平面。这是交比不对造成的。后期我们将论述另一个重要概念：交比。

 图五 按照射影几何，棋盘格的标准画法

                                                                         

四、结论

        本篇我们引入重要的射影几何概念，告诉大家在射影几何中，空间域是如何定义的。注意这种定义是逻辑的，或抽象的，然而不是不合理的，学习者需要习惯。