素数的计数律：Π函数、歪斜数

本文链接：https://blog.csdn.net/gongdiwudu/article/details/137178183

本文探讨了素数计数函数π(n)的理论与历史，介绍了Li(N)作为近似值的两种形式，以及Littlewood和Skewes关于素数函数不等式翻转的重要贡献。尽管这些数学成果具有挑战性和理论价值，但在实际应用上受限于计算能力。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述
相当多的数字！

一、说明

自从人类开始掌握最起码的算术概念以来，有一类数字一直处于最前沿——素数。素数定义简单，但难以捕捉，众所周知，素数是数学中一些最困难问题的罪魁祸首，让几代最优秀的数学家感到困惑。

“直到今天，数学家们都徒劳地试图在素数序列中发现某种秩序，我们有理由相信这是一个人类思维永远无法穿透的奥秘。” ~ 莱昂哈德·欧拉

二、素数（Prime）计数功能

也许这些问题中最著名的是这样的——给定一个数字 n，找到一个输出小于或等于 n 的素数的函数。所需的函数表示为 π（n）。

例如–

π(10) = 4 (2, 3, 5, 7)
π(17) = 7 (2, 3, 5, 7, 11, 13, 17)

π（n）， 1 ≤ n ≤ 60.来源。

在这里插入图片描述

长期以来，寻找 π（n）的闭合形式（精确）表达式一直是数学中最令人垂涎的问题之一。虽然没有人能够想出一个精确的表达式，但我们已经发现了一些强大的近似值！

三、素数计数函数的近似值

首先，谈谈我们在这里所说的近似值的含义。当我们说函数 f 近似于函数 g 时，这意味着对于足够大的 n 值，f（n）和 g（n）几乎相同，即出于实际目的，它们值之间的百分比差异可以安全地忽略（感兴趣的读者可以进一步查找 Big O 表示法）。即 f（n） ~ g（n）对于大 n。

现在，我们介绍素数函数的两个最著名的近似值。

3.1 第一个近似

1） N/lnN：这里，ln 是自然对数，即以 e 为底的对数。这是素数函数的最简单近似值。令人惊讶的是，这种直截了当的表达式产生的值与 π（n）非常吻合。此外，表达式通常输出小于 π（n）的值，从而用作 π（n）的非正式下限。
在这里插入图片描述

3.2 第二个近似函数

Li（N）：第二个近似值是对数积分。此函数定义为
在这里插入图片描述

从图形上看，它是曲线 1/ln（x）和 x 轴之间的面积，x 的范围从 2 到 N。

在这里插入图片描述

Li（N）等于曲线 1/ln（x）和 x 轴之间的面积，x 的范围从 2 到 N。
与前面的表达式不同，Li（N）通常输出大于 π（n）的值，从而作为 π（n）的非正式上限。

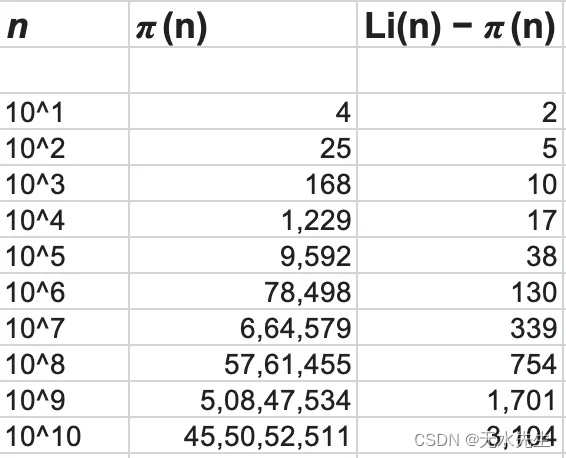
在这里插入图片描述

现在是有趣的部分。注意到上述陈述中使用了“正常”和“非正式”这两个词吗？他们是故意雇用的。请允许我详细阐述这两个词的重要性——

“通常”：这意味着这些陈述对于我们出于实际目的所关注的典型价值范围是正确的，没有矛盾。
“非正式”：但是没有数学证明这些陈述在任何地方都成立，即一直到无穷大。
那么，仅限于讨论 Li（N），对于一些较大的 N 值，它是否可能低于 π（N）？如果是，N 的值是多少？这正是本文的主要议程！

四、利特尔伍德的结果

在发现 Li（n）作为 π（n）的近似值后的许多年里，以下问题一直没有得到解答，困扰着当时最优秀的头脑——

Li（n）是否> π（n）适用于每个可能的 n？还是不平等在某个地方翻转？

人们已经尽可能高地计算了Li（n）值，但仍然没有一个反例被偶然发现。也许，许多人会认为不等式对 n 的所有值都成立。

最后，这个问题由当时英国领先的数学家之一 J.E. Littlewood 解决了——并且得到了肯定的解决！利特尔伍德证明了不等式确实翻转了某个足够大的 N 的符号，即存在一个 N，使得 Li（N） < π（N）。事实上，利特尔伍德证明了更多。他证明了不等式无限多次翻转符号！也就是说，如果我们看得足够高，我们会发现无限多的斑块，其中 Li（N）占主导地位 π（N），反之亦然。确实有相当大的结果！
在这里插入图片描述
J.E.利特尔伍德（1885-1977）。来源。
但是，无论利特尔伍德的结果多么辉煌，它都缺少一件事——第一次翻转何时发生。其结果是数学中存在论证明的经典例子——断言某物存在，而没有指定任何特定的例子，甚至没有指定构建一个算法。

因此，即使在利特尔伍德取得重大进展之后，问题仍然存在——不平等何时会出现翻转迹象？我们至少可以有一些上限吗？

确切地说，这就是留给 Littlewood 的学生 Skewes 来演示的！

五、歪斜数

在这里插入图片描述

斯坦利·斯凯斯（1899-1988）。来源。
斯坦利·斯凯斯（Stanley Skewes，1899-1988 年）是一位南非数学家，曾在剑桥大学师从利特尔伍德。在最初获得土木工程学位后，他移居英国学习数学，并于 1938 年获得博士学位。

Skewes 数是 Littlewood 发现的翻转的上限。也就是说，我们可以确定，对于某个小于 Skewes 数的数字，π（n）会大于 Li（n）！

从理论上讲，不只有一个唯一的 Skewes 数。相反，其中有两个，取决于黎曼假设的有效性。对于外行来说，黎曼假设是整个数学中最令人垂涎的开放性问题，更不用说数论了。虽然深入探讨问题的细节超出了本文的范围，但以下理解就足够了——

第一歪斜数：假设黎曼假设为真，Skewes 在 1933 年表明，必须有一个小于 10^（10（10³⁴））的数字，其中 π（n）大于 Li（n）。通常，这个数字简称为 Skewes 数。难怪人们怀疑翻转是否真的发生了！即使对于今天强大的计算机来说，如此庞大的规模的计算也是无法实现的，更不用说一个世纪前的设备了。
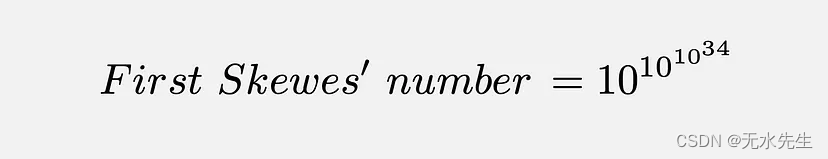
第二个 Skewes 数：如果黎曼假设是错误的，Skewes 还需要 22 年才能提出相应的极限。他 1955 年的结果证明，即使黎曼假设是错误的，π（n）和 Li（n）之间的翻转也必须发生在 10^（10（10⁹⁶⁴））以下的某个地方。这是第二个 Skewes 的数字，显然比第一个更大！