常用导航坐标系 及 转换关系 （理论+程序）

一、坐标系定义与符号约定

在捷联惯导中，涉及到多种坐标系，其中 惯性坐标系、地心地固坐标系、导航坐标系 的示意图如下：

下面给出常用的坐标系的定义 ：

1）惯性坐标系（i 系）：

以地球质心为原点， 轴指向地球自转轴， 轴位 于赤道面指向空间任意点， 轴与其构成右手系。

该坐标系不随地球自转而转动， 但是由于地球质心绕太阳公转以及太阳系绕银河系公转，因此，该系

不是绝对惯 性系， 然而这些影响十分微弱，低于惯导的噪声水平， 因而可以忽略不计，该系 可以认

为 是一个惯性系。

2）地心地固系（e 系）：

与大地测量中的 ECEF 系一致

理解：某一时刻，载体在e系中的坐标 在 i 系的表达，可通过方向余弦矩阵（ Direction Cosine Matrix, DCM）

实现，其表达如下：

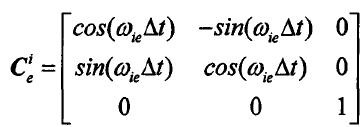
3）地理坐标系 （Geographic Coordinate System）：

是使用三维球面来定义地球表面位置，以实现通过 经纬度 对地球表面点位引用的坐标系。

一个地理坐标系包括 角度测量单位、本初子午线和参考椭球体三部分。在球面系统中，水平线是等

纬度线或纬线。垂直线是等经度线或经线。地理坐标系依据其所选用的本初子午线、参考椭球的不

同而略有区别。地理坐标系可以确定地球上任何一点的位置。首先将地球抽象成一个规则的逼近原

始自然地球表面的椭球体，称为参考椭球体，然后在参考椭球体上定义一系列的经线和纬线构成经

纬网，从而达到通过经纬度来描述地表点位的目的。需要说明的是经纬地理坐标系不是平面坐标系，

因为度不是标准的长度单位，不可用其直接量测面积长度。

地理坐标系 与 地心地固系（e 系）之间的转换关系如下：

程序如下：

Eigen::MatrixXd llh2ecef(Eigen::MatrixXd data) // transform the llh to ecef
{
  Eigen::MatrixXd ecef; // the ecef for output
  ecef.resize(3, 1);
  double a = 6378137.0;
  double b = 6356752.314;
  double n, Rx, Ry, Rz;
  double lon = (double)data(0) * 3.1415926 / 180.0; // lon to radis
  double lat = (double)data(1) * 3.1415926 / 180.0; // lat to radis
  double alt = (double)data(2); // altitude
  n = a * a / sqrt(a * a * cos(lat) * cos(lat) + b * b * sin(lat) * sin(lat));
  Rx = (n + alt) * cos(lat) * cos(lon);
  Ry = (n + alt) * cos(lat) * sin(lon);
  Rz = (b * b / (a * a) * n + alt) * sin(lat);
  ecef(0) = Rx; // return value in ecef
  ecef(1) = Ry; // return value in ecef
  ecef(2) = Rz; // return value in ecef
  return ecef;

  /**************for test purpose*************************
  Eigen::MatrixXd llh;
  llh.resize(3, 1);
  Eigen::MatrixXd ecef;
  ecef.resize(3, 1);
  llh(0) = 114.1772621294604;
  llh(1) = 22.29842880200087;
  llh(2) = 58;
  ecef = llh2ecef(llh);
  cout << "ecef ->: " << ecef << "\n";
  */
}



/*
function: ecef to llh
input: ecef (Matrix3d)
output: llh (Matrix3d)
*/
Eigen::MatrixXd ecef2llh(Eigen::MatrixXd data) // transform the ecef to llh
{
  Eigen::MatrixXd llh; // the ecef for output
  double pi = 3.1415926; // pi
  llh.resize(3, 1);
  double x = data(0); // obtain ecef 
  double y = data(1);
  double z = data(2);
  double x2 = pow(x, 2);
  double y2 = pow(y, 2);
  double z2 = pow(z, 2);

  double a = 6378137.0000; //earth radius in meters
  double b = 6356752.3142; // earth semiminor in meters
  double e = sqrt(1 - (b / a) * (b / a));
  double b2 = b*b;
  double e2 = e*e;
  double  ep = e*(a / b);
  double  r = sqrt(x2 + y2);
  double  r2 = r*r;
  double  E2 = a * a - b*b;
  double F = 54 * b2*z2;
  double G = r2 + (1 - e2)*z2 - e2*E2;
  double c = (e2*e2*F*r2) / (G*G*G);
  double s = (1 + c + sqrt(c*c + 2 * c));
  s = pow(s, 1 / 3);
  double P = F / (3 * ((s + 1 / s + 1)*(s + 1 / s + 1)) * G*G);
  double Q = sqrt(1 + 2 * e2*e2*P);
  double ro = -(P*e2*r) / (1 + Q) + sqrt((a*a / 2)*(1 + 1 / Q) - (P*(1 - e2)*z2) / (Q*(1 + Q)) - P*r2 / 2);
  double tmp = (r - e2*ro)*(r - e2*ro);
  double U = sqrt(tmp + z2);
  double V = sqrt(tmp + (1 - e2)*z2);
  double zo = (b2*z) / (a*V);

  double height = U*(1 - b2 / (a*V));

  double lat = atan((z + ep*ep*zo) / r);

  double temp = atan(y / x);
  double long_;
  if (x >= 0)
    long_ = temp;
  else if ((x < 0) && (y >= 0))
    long_ = pi + temp;
  else
    long_ = temp - pi;
  llh(0) = (long_)*(180 / pi);
  llh(1) = (lat)*(180 / pi);
  llh(2) = height;
  return llh;

  /**************for test purpose*************************
  Eigen::MatrixXd ecef;
  ecef.resize(3, 1);
  Eigen::MatrixXd llh;
  llh.resize(3, 1);
  ecef(0) = -2418080.9387265667;
  ecef(1) = 5386190.3905763263;
  ecef(2) = 2405041.9305451373;
  llh = ecef2llh(ecef);
  cout << "llh ->: " << llh << "\n";
  */
}

4）当地水平坐标系（L 系）：

原点位于载体质心， 轴沿参考椭球卯酉圈 指向东 E ， 轴沿参考椭球子午线指向北 N ， 轴沿参考椭

球法线指向天 U ， 从而形成 ENU 坐标系

5）导航坐标系（n 系）：

是惯性导航算法的基本参考系，运动物体在导航坐标系内进行位置，速度，姿态确 定，可选取 e 系

或 L 系做为导航系。 在 e 系内导航，可以直接确定地心地固系下 的导航参数， 便于和 GNSS 等大地

测量手段相结合，且动态模型简单，但不 利于 本质规律的研究。而在 L 系下导航，物理意义明确，

便于理论分析和误差规律探 寻，利于内部控制， 但动态模型复杂， 且不能直接与 GNSS 等大地测量

手段相结 合。对于组合导航解算，应选用 e 系，而对于理论分析，应选用 L 系；

一般采用当地水平坐标系 L，采用 NED 坐标系作为导航坐标系

6）载体坐标系（b 系）：

捷联惯导硬件内部定义了坐标系，其原点一般位于 硬件中心，而惯性元件安装在三个正交方向上形成

XYZ 轴。 将捷联惯导安装在 载体上后， 惯导硬件的坐标系就成为载体的坐标系，两者固联在一起。

一般将 Z 轴朝上， Y 轴朝前进方向， X 轴沿前进方向朝右

7）平台坐标系（p 系）、

在平台式惯导中，惯导通过自身调节，始终维持为 一个水平指北平台，这个就是 p 系，但由于各种

误差的影响， p 系与真实的 L 系 并不重合， 两者存在一个失准角 。在捷联惯导中，这种平台由计算

平台所取代，计算平台由 b 系转向 n 的姿态矩阵 来维持，由于解算误差的存在，所计算得 到的是存

在失准角的姿态矩阵 ， 与 存在一个失准角 。

8）计算机坐标系（c 系）：

L 系是由实际经纬度确定的当地坐标系，而惯导 自身可以解算出带有误差的经纬度 和 ，由 和 确定的

当地坐标 系称为计 算机坐标系。 c 系实质是模型简化过程中衍生出来的一个坐标系，并没有具体的

物理解释，在后续导 出 角误差模型时会详细说明。 在推导惯导误差模型时， 清晰自明的符号约定是十

分重要的，符号的混淆与 定义 不一致往往导致很多文献结果的不一致， 在相互引用时不能自洽。 

二、坐标系旋转

描述两个坐标系之间的旋转关系可以采用欧拉角、旋转矩阵、四元数和旋转 矢量四种数学工具 [57] 。

欧拉角 和旋转矩阵有密切关系， 两者统称为转角系统。 转角系统定义有如下 3 个要素：​​​​​​​1）旋转顺序；

2 ）欧拉角的 符号与域值定义； 3 ）奇点问题。  转角系统定义如图 3.2 ：

旋转顺序为 Z -> X -> Y ，第一次绕 Z 轴旋转 ，称为航向角 Yaw，第二次 X 绕 轴旋转 ，称为俯仰角 Pitch，

第三次绕 Y 轴旋转 ，称为翻滚角 Roll。 得 到的单轴旋转矩阵分别为：

欧拉角的值域为：

 

三、程序

大地坐标系(WGS-84)、地心地固坐标系(ECEF) 与 东北天坐标系(ENU)的相互转换C语言代码 

Eigen::MatrixXd ecef2enu(Eigen::MatrixXd originllh, Eigen::MatrixXd ecef) // transform the ecef to enu 
{
  double pi = 3.1415926; // pi 
  double DEG2RAD = pi / 180.0;
  double RAD2DEG = 180.0 / pi;

  Eigen::MatrixXd enu; // the enu for output
  enu.resize(3, 1); // resize to 3X1
  Eigen::MatrixXd oxyz; // the original position 
  oxyz.resize(3, 1); // resize to 3X1

  double x, y, z; // save the x y z in ecef
  x = ecef(0);
  y = ecef(1);
  z = ecef(2);

  double ox, oy, oz; // save original reference position in ecef
  oxyz = llh2ecef(originllh);
  ox = oxyz(0); // obtain x in ecef 
  oy = oxyz(1); // obtain y in ecef
  oz = oxyz(2); // obtain z in ecef

  double dx, dy, dz;
  dx = x - ox;
  dy = y - oy;
  dz = z - oz;

  double lonDeg, latDeg, _; // save the origin lon alt in llh
  lonDeg = originllh(0);
  latDeg = originllh(1);
  double lon = lonDeg * DEG2RAD;
  double lat = latDeg * DEG2RAD;

  //save ENU
  enu(0) = -sin(lon) * dx + cos(lon) * dy;
  enu(1) = -sin(lat) * cos(lon) * dx - sin(lat) * sin(lon) * dy + cos(lat) * dz;
  enu(2) = cos(lat) * cos(lon) * dx + cos(lat) * sin(lon) * dy + sin(lat) * dz;
  return enu;

  /**************for test purpose*****suqare distance is about 37.4 meters********************
  Eigen::MatrixXd llh;  //original
  llh.resize(3, 1);
  llh(0) = 114.1775072541416;
  llh(1) = 22.29817969722738;
  llh(2) = 58;
  Eigen::MatrixXd ecef;
  ecef.resize(3, 1);
  ecef(0) = -2418080.9387265667;
  ecef(1) = 5386190.3905763263;
  ecef(2) = 2405041.9305451373;
  Eigen::MatrixXd enu;
  enu.resize(3, 1);
  enu = ecef2enu(llh, ecef);
  cout << "enu ->: " << enu << "\n";
  */
}

/*
function: ecef to enu
input: original llh, and current ecef (Matrix3d)
output: enu (Matrix3d)
*/
Eigen::MatrixXd enu2ecef(Eigen::MatrixXd originllh, Eigen::MatrixXd enu) // transform the ecef to enu 
{
  // enu to ecef
  double  e = enu(0);
  double  n = enu(1);
  double  u = enu(2);
  double lon = (double)originllh(0) * D2R;
  double lat = (double)originllh(1) * D2R;
  Eigen::MatrixXd oxyz; // the original position 
  oxyz.resize(3, 1); // resize to 3X1
  oxyz = llh2ecef(originllh);
  double ox = oxyz(0);
  double oy = oxyz(1);
  double oz = oxyz(2);

  oxyz(0) = ox - sin(lon) * e - cos(lon) * sin(lat) * n + cos(lon) * cos(lat) * u;
  oxyz(1) = oy + cos(lon) * e - sin(lon) * sin(lat) * n + cos(lat) * sin(lon) * u;
  oxyz(2) = oz + cos(lat) * n + sin(lat) * u;
  return oxyz;
}

感谢：大地坐标系(WGS-84)、地心地固坐标系(ECEF)与东北天坐标系(ENU)的相互转换C语言代码分享_Schroeder1_新浪博客