目录
概述
本文主要介绍离散化PID算法的实现原理,以方便对其进行数字化的处理,重点介绍位置式PID算法和增量式PID算法的离散化实现原理。还介绍了调整PID参数的常用方法。
1 背景介绍
由于计算机的出现,计算机进入了控制领域。人们将模拟 PID 控制规律引入到计算机中来。对下式中 PID 控制规律进行适当的变换,就可以用软件实现 PID 控制,即数字 PID 控制。
模拟PID公式:
Kp ―― 控制器的比例系数
Ti ―― 控制器的积分时间,也称积分系数
Td ―― 控制器的微分时间,也称微分系数e(t) PID 控制的输入
2 数字式 PID 控制算法
数字式 PID 控制算法可以分为位置式 PID 和增量式 PID 控制算法。
2.1 位置式 PID
由于计算机控制是一种采样控制, 它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量量, 进行连续控制。 由于这一特点中的积分项和微分项不能直接使用,必须进行离散化处理。离散化处理的方法为:以T 作为采样周期, 作为采样序号,则离散采样时间 kT对应着连续时间t , 用矩形法数值积分近似代替积分, 用一阶后向差分近似代替微分, 可作如下近似变换:
离散PID公式
上式中,为了表示的方便,将类似于e(kT )简化成ek 等。根据模拟PID公式和离散PID公式的关系,就可以得到离散的 PID 表达式为:
或
参数介绍
k ―― 采样序号, k =0, 1, 2,……;
uk ―― 第k 次采样时刻的计算机输出值;
ek ―― 第k 次采样时刻输入的偏差值;
ek-1 ―― 第k -1 次采样时刻输入的偏差值;
Ki ―― 积分系数, Ki= Kp *T Ti ;
Kd ―― 微分系数, Kd= Kp *Td T ;
上述离散PID公式表示的控制算法式直接按模拟PID公式所给出的 PID 控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式 PID 控制算法。
这种算法的缺点是:
由于全量输出, 所以每次输出均与过去状态有关, 计算时要对ek 进行累加,工作量大; 并且,因为计算机输出的 对应的是执行机构的实际位置, 如果计算机出现故障,输出的 uk将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实生产际中是不允许的。
2.2 增量式 PID
所谓增量式 PID 是指数字控制器的输出只是控制量的增量∆uk 。 当执行机构需要的控制量是量,而不是位置量的绝对数值时,可以使用增量式 PID 控制算法进行控制。
增量式 PID 控制算法可以通过离散PID公式推导出。由离散PID公式可以得到控制器的第 k-1
个采样时刻的输出值为:
可以推出公式:
其中
由上式可以看出,如果计算机控制系统采用恒定的采样周期T ,一旦确定 A、 B、 C,只要使用前后三次测量的偏差值,就可以由上式求出控制量。
2.3 两种算法比较
增量式 PID 控制算法与位置式 PID 算法相比,计算量小的多,因此在实际中得到广泛的应用。而位置式 PID 控制算法也可以通过增量式控制算法推出递推计算公式:
3 控制器参数整定
控制器参数整定: 指决定调节器的比例系数 Kp 、 积分时间Ti 、 微分时间Td 和采样周期Ts 的具体数值。 整定的实质是通过改变调节器的参数,使其特性和过程特性相匹配, 以改善系统的动态和静态指标,取得最佳的控制效果。整定调节器参数的方法很多, 归纳起来可分为两大类, 即理论计算整定法和工程整定法。 理论计算整定法有对数频率特性法和根轨迹法等; 工程整定法有凑试法、 临界比例法、经验法、 衰减曲线法和响应曲线法等。 工程整定法特点不需要事先知道过程的数学模型,直接在过程控制系统中进行现场整定方法简单、计算简便、易于掌握。
3.1 凑试法
按照先比例(P)、再积分(I)、最后微分(D)的顺序。置调节器积分时间Ti =∞, 微分时间Td =0, 在比例系数 按经验设置的初值条件下, 将系统投入运行,由小到大整定比例系数 。求得满意的 1/4 衰减度过渡过程曲线。Kp引入积分作用(此时应将上述比例系数 Kp 设置为 5/6 Kp )。将Ti 由大到小进行整定。若需引入微分作用时,则将Td 按经验值或按Td =(1/3~1/4) Ti 设置,并由小到大加入。
3.2 临界比例法
在闭环控制系统里, 将调节器置于纯比例作用下, 从小到大逐渐改变调节器的比例系数, 得到等幅振荡的过渡过程。 此时的比例系数称为临界比例系数 , 相邻两个波峰间的时间间隔, 称为临界振荡周期Tu 。
临界比例度法步骤:
1、将调节器的积分时间 置于最大( Ti =∞),微分时间置零( Td =0),比例系数 适当,平衡操作一段时间,把系统投入自动运行。
2、 将比例系数 Kp 逐渐增大, 得到等幅振荡过程, 记下临界比例系数 Ku 和临界振荡周期Tu值。
3、根据 Ku 和Tu 值,采用经验公式,计算出调节器各个参数,即 Kp 、 Ti 和Td 的值。按“先 P 再 I 最后 D”的操作程序将调节器整定参数调到计算值上。若还不够满意,可再作进一步调整。
临界比例度法整定注意事项:
1)有的过程控制系统, 临界比例系数很大, 使系统接近两式控制, 调节阀不是全关就是全开,对工业生产不利。
2)有的过程控制系统, 当调节器比例系数 调到最大刻度值时, 系统仍不产生等幅振荡,对此,就把最大刻度的比例度作为临界比例度 进行调节器参数整定。
3.3 经验法
用凑试法确定 PID 参数需要经过多次反复的实验, 为了减少凑试次数, 提高工作效率, 可以借鉴他人的经验, 并根据一定的要求, 事先作少量的实验, 以得到若干基准参数, 然后按照经验公式,用这些基准参数导出 PID 控制参数,这就是经验法。临界比例法就是一种经验法。 这种方法首先将控制器选为纯比例控制器, 并形成闭环, 改变比例系数,使系统对阶跃输入的响应达到临界状态,这时记下比例系数 Ku 、临界振荡周期为Tu 。
4 参数调整规则的探索
人们通过对 PID 控制理论的认识和长期人工操作经验的总结, 可知 PID 参数应依据以下几点来适应系统的动态过程。
1、 在偏差比较大时, 为使尽快消除偏差, 提高响应速度, 同时为了避免系统响应出现超调, Kp取大值, 取零;在偏差比较小时,为继续减小偏差,并防止超调过大、产生振荡、稳定性变坏,值要减小, 取小值; 在偏差很小时,为消除静差,克服超调,使系统尽快稳定, 值继续减小, 值不变或稍取大。
2、当偏差与偏差变化率同号时,被控量是朝偏离既定值方向变化。因此,当被控量接近定值时,反号的比列作用阻碍积分作用,避免积分超调及随之而来的振荡,有利于控制;而当被控量远未接近各定值并向定值变化时,则由于这两项反向,将会减慢控制过程。在偏差比较大时, 偏差变化率与偏差异号时, Kp 值取零或负值,以加快控制的动态过程。
3、偏差变化率的大小表明偏差变化的速率, 越大, 取值越小, 取值越大,反之亦然。同时,结合偏差大小来考虑。
4、微分作用可改善系统的动态特性,阻止偏差的变化,有助于减小超调量,消除振荡,缩短调节时间 ,允许加大 ,使系统稳态误差减小,提高控制精度,达到满意的控制效果。所以,在 比较大时, 取零,实际为 PI 控制;在 比较小时, 取一正值,实行 PID 控制。











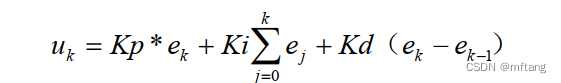



















 2326
2326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








