同时校准移动机器人的里程表和传感器参数

最新推荐文章于 2024-03-25 18:19:38 发布

hello我是小菜鸡

最新推荐文章于 2024-03-25 18:19:38 发布

阅读量5.1k

点赞数 8

分类专栏： slam学习文章标签：里程计雷达同时标定

slam学习专栏收录该内容

2 篇文章 2 订阅

订阅专栏

Simultaneous calibration of odometry and sensor parameters for mobile robots，Andrea Censi, Student Member, Antonio Franchi, Member, Luca Marchionni, and Giuseppe Oriolo, Senior Member，2013， IEEE Transactions on Robotics

摘要：

细想有一个差速器驱动的移动机器人，它装备了一个可以估计自身运动的捷联外部感受传感器，例如激光雷达。这个机器人的校准估计6个参数：3个用于里程测量参数(半径和车轮之间的距离)，3个用于传感器相对于机器人的姿态测量参数。在分析了该问题的可观测性后，本文提出了一种不需要额外的外部传感器或设备，只需要测量车轮速度和外部感受传感器的数据，即可同时校准所有参数的方法。此外，该方法不需要机器人沿着特定的轨迹移动。将同时标定问题表示为极大似然问题，并求闭式解。实验结果表明，该标定方法的精度非常接近可达到的极限。

引言：

机器人系统的运行需要先验的参数知识，这些参数描述了传感器和执行器的特性及配置。这些参数通常分为内部参数和外部参数。所谓内参，通常是指那些与单个传感器或执行器相关联的参数。内参包括里程表参数，或针孔相机的焦距。外参描述传感器/执行器之间的关系，例如它们的参考系的相对位置。

本文阐述、分析并解决了一个由差速器驱动机器人的里程计固有参数和机器人平台与能够估计差速器自身位置的外征传感器之间的标定问题。所用方法可用于对最常见的机器人构型的所有相关参数进行从零开始标定，不需要外部传感器或预先信息。为了正确看待这一贡献，我们简要回顾了相关文献，从最常见的里程计校准方法开始。

A.里程计校准相关工作

Doebbler等人的[1]表明，如果轮式平台有足够多的来自脚轮的额外测量，那么仅使用内部里程测量就可以估计校准参数。最常见的方法是使用额外传感器的测量值。例如，Von der Hardt等人展示了额外的内部传感器，如陀螺仪和罗盘，可以用于里程表校准[2]。最流行的方法是沿着特别设计的轨迹驱动机器人，通过外部传感器对其姿态进行一些外部测量，然后根据估计参数中的误差如何影响最终姿态的知识，纠正对里程表参数的首次估计。该方法由Borenstein和Feng率先提出，采用UMBmark方法[3]，在该方法中，一个差速器驱动机器人沿着一个正方形的路径，顺时针和逆时针方向重复驱动，并对最终姿态进行外部测量;根据最后的误差，里程表中三个自由度中的两个可以得到修正。同样，Kelly[4]将该过程推广到任意轨迹和不同的运动学。

另一种方法是将里程计校准描述为一个滤波问题。一种可能性是使用扩展卡尔曼滤波器(EKF)来估计机器人的姿态和里程表参数，如Larsen等人的[5]，Caltabiano等人的[6]和Martinelli等人的[7]。Foxlin[8]对该思想进行了推广，其中滤波器状态向量包含传感器参数、机器人配置和环境映射;进一步的研究(特别是后来讨论的Martinelli的研究)表明，在考虑如此大且异构的系统时，必须注意可观测性问题，因为并非总是完整的状态是可观测的。

滤波的另一种方法是解决优化问题，通常采用最大似然估计的形式。Roy和Thrun[9]提出了一种在线估计差分驱动机器人简化里程模型参数的方法。Antonelli et al.[10]，[11]利用外部摄像机的绝对观测值，采用极大似然法估计差速器驱动机器人的测程参数。该方法特别简单，因为问题是线性的，因此可以用线性最小二乘来解决。Antonelli和Chiaverini[12]表明，同样的问题可以用确定性滤波器(非线性观测器)来解决，得到了大致相同的结果。

有必要指出两种方法之间的一些普遍差异。UMBmark-和ekf类方法假定参数的标称值是先验已知的，估计的调整量相对较小。对于EKF，通常需要注意的是：线性化误差可能非常大，要减轻数据中的异常值(例如，来自车轮打滑)的影响可能很困难。非线性观测器具有比EKF更简单的收敛性和误差有界性证明，但不提供不确定性的估计。离线极大似然问题具有易处理离群值的特点，不受线性化的影响，但每一种情况都需要一个特殊的解，因为得到的优化问题通常是非线性和非凸的。

B.外部传感器标定相关工作

在机器人技术中，如果将车载传感器安装在机器人上，除了测程参数外，还必须估计传感器相对于机器人框架的姿态，这是在将测程数据与传感器数据融合到定位和映射等问题之前的一个初步步骤。在相关领域，对外感受传感器的外标定问题进行了深入的研究;例如，摄像机或立体钻机的标定是计算机视觉中的一个典型问题。对相机+ (3D)测距仪[13][15]等异构传感器也进行了研究。

Martinelli和Scaramuzza[16]考虑了轴承传感器姿态的标定问题，结果表明，由于存在不可避免的尺度不确定性，系统不能完全被观测到。Martinelli和Siegwart[17]描述了不同传感器和运动学组合的可观测性。结果并不总是直观的，这激发了后续工作来正式证明所研究系统的可观测性。

Mirzaei和Roumeliotis[18]使用扩展卡尔曼滤波器研究了摄像机和IMU的标定问题。hech等人考虑了用最大似然公式对镜面进行观测来估计相机姿态的问题。Underwood等人[20]、Brookshir和Teller[21]考虑了在移动机器人上校准多个外部感受传感器的问题。

C.同时校准里程表和外感受传感器

同时标定里程计和传感器的姿态是一个鸡生蛋还是蛋生鸡的问题。事实上，用于标定传感器位姿的方法假定里程表已经标定，而标定里程表的方法假定已知传感器位姿(或存在额外的外部传感器)。同时标定这两个问题是一个比较复杂的问题，不能分解为两个子问题。

在[22]中，我们提出了第一个工作(据我们所知)处理联合校准的内在测程参数和外在传感器的姿态。特别地，我们考虑了一个装有测距仪的差动驱动机器人，或者，一般来说，任何能估计其自身位置的传感器。这是机器人中非常常见的配置。后来，Martinelli[23]考虑了差动驱动机器人的同时标定加上一个轴承传感器的姿态，该传感器返回一个点特征所在的角度。从数学上讲，这是一个非常不同的问题，因为正如Martinelli所示，系统是不可观测的，而轴承传感器的姿态只能在一定的范围内恢复。最近，Martinelli[24]在对状态不能完全重建的估计问题进行一般性处理的背景下重新讨论了相同的问题。介绍连续对称性的概念来描述这种情况下,在相同的对称性精神研究在理论物理和力学对称(通常是一个谎言的作用的同义词组)，但推导一切使用机械的理论分布应用于非线性控制理论。Antonelli et al.[25]假设已知环境中的某个地标配置，考虑将里程计与机载摄像机的内外参数一起校准的问题。

在[22]中提出的方法有几个有趣的特点：机器人沿着任意轨迹自主驱动，不需要外部测量，也不需要事先测量标称参数。此外，作为一个静态最大似然问题的公式允许检测和过滤异常值。

本论文是该工作的延伸。对于原论文，我们给出了一个非线性和随机可观测性分析，证明了系统是局部可观测的，以及全局对称性的一个完整刻画(第三节)；更仔细地处理一些简化假设(第V-B1节)；更全面的实验数据，加上基于Cramer Rao界(Section VI)的不确定性和最优性分析。附加的多媒体材料包括c++实现和实验中使用的数据文件。

二、问题的定义

图1.机器人相对于世界坐标系姿态为qkl；传感器相对于机器人的姿态为l；rk为机器人在姿态间的位移；sk 是传感器在自身参考系中看到的位移。

SE(2)是平面运动的特殊欧式群，se(2)是其相应的李代数。假设： $q=(q_{x}, q_{y}, q_{\theta }) \in SE(2)$ ，作为机器人相对于固定的世界坐标系的一个姿态。对于差速机器人，可以根据微分方程进行变化：

$\dot{q}=\left ( \begin{matrix} cos q_{\theta } & 0\\ sin q_{\theta } & 0 \\ 0 & 1 \end{matrix} \right )\left ( \begin{matrix} v\\ w \end{matrix} \right )$ （1）

驱动速度 $v$ 和转向速度 $\omega$ 取决于左右轮差速 $\omega _{L},\omega _{R}$ ，这里存在一个线性转换：

$\left ( \begin{matrix} v\\ \omega \end{matrix} \right )=J\left ( \begin{matrix} \omega_{L}\\ \omega_{R} \end{matrix} \right )$ （2）

转换矩阵 $J$ 是机器人参数 $r_{L},r_{R},b$ 的一个函数， $J$ 的定义如下所示：

$J=\left ( \begin{matrix} J_{11} & J_{12}\\ J_{21} & J_{22} \end{matrix} \right )=\left ( \begin{matrix} +r_{L}/2 & +r_{R}/2\\ -r_{L}/b & +r_{R}/b \end{matrix} \right )$ （3）

其中， $r_{L},r_{R}$ 分别是左右轮的轮径， $b$ 是左右轮的轮距。我们假设能够测量左右轮的转速 $\omega _{L},\omega _{R}$ 。我们不假定能够设定车轮速度；这种方法是完全被动的。如果它满足必要的兴奋性条件，可以适用于任何轨迹，在下一节概述。

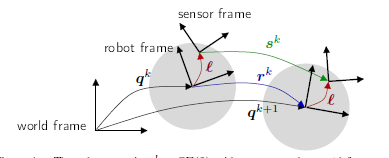
我们还假设在机器人平台上有一个水平安装的外感受传感器(俯仰和横滚为零，只感受偏航)。在此基础之上，传感器相对于机器人参考系的位姿可以表示为 $l=\left ( \begin{matrix} l_{x} & l_{y} & l_{\theta } \end{matrix} \right ) \in SE(2)$ （图1所示）。因此，任意时刻 $t$ ，传感器在世界坐标系中的位姿为 $q\left ( t \right )\oplus l$ 。这里 $\oplus$ 表示 $SE(2)$ 的李群运算。表1定义了 $\oplus$ 和 $\circleddash$ 在 $SE(2)$ 中的运算

表1.李群算子说明
$\oplus$	$\left ( \begin{matrix} a_{x}\\ a_{y}\\ a_{\theta } \end{matrix} \right )\oplus \left ( \begin{matrix} b_{x}\\ b_{y}\\ b_{\theta } \end{matrix} \right )=\left ( \begin{matrix} a_{x}+b_{x}cos(a_{\theta })-b_{y}sin(a_{\theta })\\ a_{y}+b_{x}sin(a_{\theta })+b_{y}cos(a_{\theta })\\ a_{\theta }+b_{\theta } \end{matrix} \right )$
$\circleddash$	$\circleddash \left ( \begin{matrix} a_{x}\\ a_{y}\\ a_{\theta } \end{matrix} \right )=\left ( \begin{matrix} -a_{x}cos(a_{\theta })-a_{y}sin(a_{\theta })\\ a_{x}sin(a_{\theta })-a_{y}cos(a_{\theta })\\ -a_{\theta } \end{matrix} \right )$

外在的观察自然是一个离散的过程 $m^{k}$ ：观测可以在一组时间序列上： $t_{1}<...<t_{k}<...<t_{n}$ ，这组序列一般不是均匀分布的。就假如第k个时间间隔 $t\in\left [ t_{k},t_{k+1} \right ]$ ，假设机器人的初始和最终姿态分别为 $q^{k}=q(t_{k})$ 和 $q^{k+1}=q(t_{k+1})$ 。用 $s_{k}$ 表示传感在区间 $t\in\left [ t_{k},t_{k+1} \right ]$ 上的位移，根据图1的运动，可以用以下方程进行描述：

$s^{k}=\circleddash \left ( q^{k}\oplus l \right )\oplus \left ( q^{k+1}\oplus l \right )$

令 $r^{k}=\circleddash q^{k}\oplus q^{k+1}$ ， $r^{k}$ 可以表示为机器人在此时间间隔内的位移，传感器的位移进一步可以表示为（交换律）：

$s^{k}=\circleddash l\oplus r^{k}\oplus l$ （4）

我们假设能够估计出传感器的帧间位移 $s_{k}$ 依靠与传感器捕获的外界测量值 $m^{k},m^{k+1}$ ，并且我们能用比如激光器帧间匹配的方法得到一个 $s_{k}$ 的估计 $\hat{s}_{k}$ 。

此时，待解决的问题就可以陈述为：

问题1：同时校准：在时间 $t\in\left [ t_{1},t_{k+1} \right ]$ 区间内给定两个车轮转速 $\omega _{L}(t),\omega _{R}(t)$ ，以及与外部在时间序列 $t_{1}<...<t_{k}<...<t_{n}$ 上的传感器观测估计 $\hat{s}_{k}$ ，为 $r_{L},r_{R},b,l_{x},l_{y},l_{\theta }$ 找到最大似然估计值。

不难发现 $s^{k}$ 就是带估计值的函数。

三、可观性分析

在解决一个估计问题之前，提供一个可观察性分析已经成为机器人领域的一个很好的习惯（但目前都是用凸优化的方式直接求解，相比较而言讨论系统可观还是可控的比较少）。通常这是根据非线性可观测性理论证明系统是局部弱可观测[27]的一个证明。要求系统为连续时间形式：

$\left\{\begin{matrix} \dot{x}=f(x,u)\\ y=g(x) \end{matrix}\right.$ （5）

其中x同时包含参数和时变状态，y为连续时间观测值。这种分析没有考虑到观测结果的不确定性。这一分析在第三- a节中进行详细描述。

另一种方法是基于费歇耳信息矩阵[28]的随机分析，在此假设系统是静态的：

$y=h(x,u)+\epsilon$ （6）

其中y是一个离散观测向量， $\epsilon$ 是伴随随机噪声。如果x的费歇尔信息矩阵是满秩的，当u被适当的选择时，系统是可观察的。这一分析见第三- b节。它的离散化特征更好地捕捉了我们校准问题的本质，这是由外部观测的可用性自然离散的。

两种分析结果一致。但是，请注意，它们都是局部的，因为它们不能解释参数空间的全局对称性；我们在第三- c节中讨论这种对称性。

A.非线性/连续的可观测性分析

为了进行分析，必须将系统置于式(5)中，其中状态x同时包含机器人姿态q和待标定的参数。这导致了两个问题：首先，(5)是一个连续观测过程为y的连续微分方程。这意味着，必须通过等效的连续观测近似估计传感器位姿位移，但是通过给定的两个连续的测量——这显然是一个自然离散的过程。其次,包括机器人位姿q作为状态向量的一部分使得很难进行可观测性分析，因为相对测量值m无法直接观测到世界坐标系中的位姿q；利用[24]的术语，该系统具有连续对称性，涵盖了位姿q的所有分量。我们展示了如何同时解决这两个问题。

我们需要找到一个和连续时间的相似的离散时间传感器在 $t\in\left [ t_{1},t_{k+1} \right ]$ 测量帧间位移 $s_{k}$ 。我们注意到，当测量之间的间隔趋于零，传感器的位移趋于传感器的速度（物理中常用的近似，在极短时间内，位移可以等效于速度）。因此，我们假设，在非线性可观测性分析的情况下，我们可以抽象出测量相速度的传感器的外部测量过程（位移不可观，但是速度可观）。

表示传感器帧内的传感器速度 $\nu =\left ( \nu_{x}, \nu_{y}, \nu_{\theta } \right ) \in se(2)$ ，（相当于用李代数表征李群）通过简单的代数(或者通过通用的帧到帧转换[26])，可以看出 $\nu$ 取决于传感器姿态和机器人速度：

$\left ( \begin{matrix} \nu _{x}\\ \nu_{y} \end{matrix} \right )=R(-l_{0})\left [ \left ( \begin{matrix} v\\ 0 \end{matrix} \right )+\left ( \begin{matrix} 0 & \omega \\ -\omega & 0 \end{matrix} \right )\left ( \begin{matrix} l_{x}\\ l_{y} \end{matrix} \right ) \right ]$ （7）

$\nu _{\theta }=\omega$

在这， $R(.)$ 代表了一个 $2\times 2$ 的旋转矩阵。这个表达式不依赖于机器人的姿态q；这是直观的，因为传感器看到的速度不依赖于机器人在世界坐标系中的绝对姿态。同样重要的是，我们可以将位姿q(t)从可观测性分析中去除(它本身是不可观测的，且不影响可观测参数的观测)。因此，在这种情况下，非线性可观测性分析导致一个退化模型，缺乏任何动力学，并易于证明可观测性。（也就是说，在不观测机器人位姿的时候，退化的系统反而具有可观性）

命题2：根据非线性连续时间可观测性分析的静态观测模型(7)，如果 $r_{L},r_{R},b\neq 0$ 时，标定参数可由两种具有线性无关等轮速轨迹的测量值得到。

证明：

观测值(7)可以写成的 $\omega _{L},\omega _{R}$ 的线性函数：

$\nu =\nu_{L}(x)\omega_{L}+\nu_{R}(x)w_{R}$

其中：

$x=(r_{L},r_{R},b,l_{x},l_{y},l_{\theta })$ ，包含了所有带估计的向量。

$\nu _{L}(x)=\left ( \begin{matrix} (J_{11}+l_{y}J_{21})cosl_{\theta }-l_{x}J_{21}sinl_{\theta }\\ -(J_{11}+l_{y}J_{21})sinl_{\theta }+l_{x}J_{21}cosl_{\theta }\\ J_{21} \end{matrix} \right )$

$\nu _{R}(x)=\left ( \begin{matrix} (J_{12}+l_{y}J_{22})cosl_{\theta }-l_{x}J_{22}sinl_{\theta }\\ -(J_{11}+l_{y}J_{22})sinl_{\theta }+l_{x}J_{22}cosl_{\theta }\\ J_{22} \end{matrix} \right )$

通过选择两个正则轨迹 $\left ( \omega_{L},\omega_{R} \right )=(1,0)$ 和 $\left ( \omega_{L},\omega_{R} \right )=(0,1)$ ，我们可以得到观测向量：

$y=\left [ \nu_{L}(x)^{T}, \nu_{R}(x)^{T} \right ]^{T}$ （8）

仅当雅可比矩阵 $\frac{\partial y}{\partial x}$ 是满秩的，这个系统是局部可观的。几个简单的代数步骤(省略)表明雅可比矩阵的行列式为 $-r_{L}^{2}r_{R}^{2}/b^{5}$ ，因此它是非奇异假设 $r_{L},r_{R},b\neq 0$ 。如果选择其他两个线性无关的轨迹，则结果不变。（实际上，这意味着是一个纯旋转的过程）

B.线性化/离散的可观测性分析

为了应用这种分析，我们应该把系统设为静态形式(6)，其中x是带估计状态，y是观测值， $\epsilon$ 是附加噪声。在接下来的几节中，我们将使用这种形式来介绍使用克拉美罗边界对给定轨迹上的估计参数的精度的定量界限。现在，我们只对显示参数是可观的感兴趣：这可以通过显示(6)中的映射h是一个局部微分同胚来实现。

命题3：根据模型的随机离散时间可观测性分析(4)， $r_{L},r_{R},b\neq 0$ 时，标定参数可由两线性无关的匀速车轮轨迹测量值得到。

证明：

本文采用实际非线性模型进行分析，观测到的位移 $s_{k}$ 由式(4)给出。假设机器人在区间 $\left [ t_{k},t_{k+1} \right ]$ 内以恒定的轮速运动。设传感器帧内对应的匀速为 $\nu ^{k} \in se(2)$ 。利用初等李群理论，我们可以把位移 $s_{k}$ 写成：在时间 $T^{k}=t_{k+1}-t_{k}$ 上初始状态 $s(0)=0$ 的微分方程 $\dot{s}(t)=s(t)\nu$ 的解（正交矩阵的逆等于其转置，该方程由 $\dot{s}(t)s(t)^{T}=\nu$ 演变而来）。这个方程的解可以写成 $s^{k}=Exp(T^{k}\nu^{k})$ ，其中Exp代表着从 $se(2)$ 到 $SE(2)$ 的指数映射。

和之前的一样，选择两个正则轨迹 $\left ( \omega_{L},\omega_{R} \right )=(1,0)$ 和 $\left ( \omega_{L},\omega_{R} \right )=(0,1)$ ，假设我们只对每条轨迹设置一个观察，它的间隔为等间隔T。这个观测向量为：

$y=\left [ Exp(T\nu_{L}(x))^{T} ,Exp(T \nu_{R}(x))^{T} \right ]^{T}$

将其与(8)进行比较，(8)在连续时间近似下等价，其中，用观测 $se(2)$ 中的速度代替观测 $SE(2)$ 中的位置。

坐标的规律性变化保证可随机可观测性。所以我们改变坐标刻度： $\tilde{y}=Exp^{-1}(y)/T$ 。这是小运动的微分同胚（对于大于或等于180度的运动，映射是不可逆的）。我们得到了虚构的观察结果 $\tilde{y}=\left [ \nu_{L}(x)^{T},\nu_{R}(x)^{T} \right ]^{T}$ 形式上与(8)相同。我们已经证明了雅可比矩阵 $\frac{\partial y}{\partial x}$ 是满秩的。因此，费歇尔信息矩阵是满秩的，所有参数都是可见的。如果选择其他两个线性无关的轨迹，则结果不变。

C.全局歧义

所提出的两种分析只具有局部有效性:它们断言有可能将真实解与其相邻解区分开来，但它们没有考虑参数空间中的全局对称性。通过观察，我们发现了这样一个全局对称性。

定理4.两套校准参数 $\left ( r_{L},r_{R},b,l_{x},l_{y},l_{\theta } \right )$ 和 $\left (- r_{L},-r_{R},-b,-l_{x},-l_{y},l_{\theta }+\pi \right )$ 是没有去别的。

证明：通过代入(7)，它们给出了相同的传感器速度，因此得到了相同的观测值。按照惯例，我们将选择带b > 0的解，这样b就有了车轮之间(正)距离的物理描述。

我们也可以证明没有其他对称。

定理5.除了命题4所描述的对称性外，没有其他的全局对称性。

证明：这个证明是“建设性的”，因为它是基于对校准方法的分析。特别地，我们将证明在考虑命题4的对称性后，极大似然问题的解具有唯一解。

四、标定问题的极大似然正式化

将问题表述为最大似然问题意味着寻找最能解释测量值的参数，并涉及到将目标函数(测量对数似然)作为参数和测量值的函数。

考虑到机器人沿任何构型轨迹运动 $q(t)$ ，通过观察 $t_{1}<...<t_{k}<...<t_{n}$ 。考虑第k个区间，机器人从姿态移动从 $q^{k}=q(t_{k})$ 到位姿 $q^{k+1}=q(t_{k+1})$ 。机器人位姿移动表示为 $r^{k}=\circleddash q^{k}\oplus q^{k+1}$ 。这个值取决于车轮速度 $\omega _{L},\omega _{R}$ 还有里程计参数，在 $t\in\left [ t_{1},t_{k+1} \right ]$ 时间内。我们还重写了(4)式，它给出了 $r^{k},s^{k},l$ 之间的约束条件，这证明里程计参数的依赖性：

$s^{k}=\circleddash l\oplus r^{k}\left ( r_{L},r_{R},b \right )\oplus l$ (9)

我们假设知道传感器位移的一个估计 $\hat{s}^{k}$ ，这个估计是个均值为 $s^{k}$ ，方差为 $\Sigma _{k}$ 的高斯分布。所以 $\jmath =logp\left ( \left \{ \hat{s}^{k} \right \} | r_{L},r_{R},b,l\right )$ 似然估计可以表示为：

$\jmath =-\frac{1}{2}\sum_{k=-1}^{n}\left \| \hat{s}^{k}-\circleddash l\oplus r^{k}\left ( r_{L},r_{R},b \right )\oplus l \right \|_{\Sigma _{k}^{-1}}^{2}$ (10)

其中， $\left \| z \right \|_{A}^{2}=z^{T}Az$ 标识的是一个向量z的A范数。我们把校准问题简化为最优化问题。

问题6：对公式10最大化 $\left ( r_{L},r_{R},b,l_{x},l_{y},l_{\theta } \right )$ 。

这个最大化问题是非凸的;因此，利用通用数值技术[29]不能有效地求解。但是，根据下一节描述的算法，我们仍然可以用封闭的形式求解。

五、计算方法

这个章节介绍了问题6的解决算法。该方法在下面的页面总结为算法1。

如果以下技术假设成立，该算法提供了问题的精确解决方案。

假设1： $s^{k}$ 的方差 $\Sigma _{k}$ 是对角矩阵且在x和y方向是各向同性的：

$\Sigma _{k}=diag\left ( \left ( \sigma _{xy}^{k} \right )^{2}, \left ( \sigma _{xy}^{k} \right )^{2},\left ( \sigma _{\theta }^{k} \right )^{2} \right )$

实际上 $\Sigma _{k}$ 最终取决于环境特性。比如在x方向上特征更少可能x方向的协方差将会长（不确定性增加）。因此，它在一定程度上是由用户控制的。

如果假设不成立，则建议使用协方差膨胀技术；这包括忽略非对角关联，并“膨胀”对角元素。比如，对于一个 $2 \times 2$ 的矩阵，我们用 $\left ( \begin{bmatrix} max(\sigma_{x} ^{2}) & 0\\ 0 & max(\sigma_{y} ^{2}) \end{bmatrix} \right )$ 替代 $\left ( \begin{bmatrix} \sigma_{x} ^{2} & \rho _{xy}\sigma _{x}\sigma _{y}\\ \rho _{xy}\sigma _{x}\sigma _{y} & \sigma_{y} ^{2} \end{bmatrix} \right )$ 。这保证所找到的估计数仍然是一致的(即，估计的协方差是实际协方差的保守近似)。

算法概括：

我们解决这个问题的计划包括以下步骤，这些步骤将在本节的其余部分中详细介绍：

A. $J_{21},J_{22}$ 的线性估计

我们证明了只考虑 $\hat{s}_{\theta }^{k}$ 的旋转值可以独立地估计 $J_{21}=-r_{L}/b,J_{22}=r_{R}/b$ 。实际上， $s_{\theta }^{k}$ 线性依赖于 $J_{21},J_{22}$ 。因此，通过线性最小二乘，可以方便、鲁棒地恢复参数。算法的第一部分相当于Antonelli等人的[10]，[11]的过程。

B.其他参数的非线性估计

1）可能性的可处理近似。

我们证明了，在假设1下，可以把（10）中 $\left \| \hat{s}^{k}-\circleddash l\oplus r^{k}\oplus l \right \|$ 写成 $\left \| l\oplus \hat{s}^{k}-r^{k}\oplus l \right \|$ ，这样更容易最小化。

2）运动学积分。

我们证明了，给定的 $J_{21},J_{22}$ ，对于任何轨迹，平移 $\left ( r_{x}^{k},r_{y}^{k} \right )$ 是轮轴长度b的线性函数。

3）约束二次优化公式。

我们采用一个技巧：将 $cosl_{\theta }$ 和 $sinl_{\theta }$ 当作两个独立的参数，这样，这允许将原始目标函数写成向量的二次函数 $\varphi =\left ( b,l_{x},l_{y}, cosl_{\theta }, sinl_{\theta } \right )^{T}$ ，这就包含了所有四个保留参数。同时，添加约束 $\varphi _{4}^{2}+\varphi _{5}^{2}=1$ 保证求解的一致性。

4）约束二次方程组的解。

证明了约束二次问题可以用闭形式求解;因此，我们可以估计参数 $\left ( b,l_{x},l_{y},l_{\theta } \right )$

5）恢复 $\left ( r_{L},r_{R} \right )$

轮子半径由 $J_{21},J_{22}$ 和b进行估计。

C.离群值删除

该算法必须集成一个离群点检测/剔除阶段，以处理滑动和其他未建模误差的来源。

D.不确定性分析

最后，利用Cramér–Rao定界估计了解的不确定性。

A. $J_{21},J_{22}$ 的线性估计：

首先，注意到约束方程（9）代表着 $s_{\theta }^{k}=r_{\theta }^{k}$ ：机器人和传感器看到相同的旋转（传感器相对旋转参数实际与机器人旋转参数一致）。

从机器人的运动学可知，机器人的旋转位移是车轮速度和里程计参数的线性函数。更准确地说，从（1-2）中，我们知道 $r_{\theta }^{k}=L_{k}\left ( \begin{matrix} J_{21}\\ J_{22} \end{matrix} \right )$ 。其中 $L_{k}$ 是一个依赖于速度地行向量：

$L_{k}=\left ( \begin{matrix} \int_{t_{k}}^{t_{k+1}}\omega_{L}(t)dt & \int_{t_{k}}^{t_{k+1}}\omega_{R}(t)dt \end{matrix} \right )$ (11)

使用 $s_{\theta }^{k}$ 的可用估计值 $\hat{s}_{\theta }^{k}$ 和标准偏差 $\sigma _{\theta }^{k}$ ， $J_{21},J_{22}$ 的估计能供通过下面的线性最小二乘方程（对于方程 $XA=Y$ ，最小二乘解为 $A=\left ( X^{T}X \right )^{-1}X^{T}Y$ ）找到：

$\left ( \begin{matrix} \hat{J}_{21}\\ \hat{J}_{22} \end{matrix} \right )=\left [ \sum_{k}\frac{L_{k}^{T}L_{k}}{\left ( \sigma _{\theta }^{k} \right )^{2}} \right ]^{-1} \sum_{k}\frac{L_{k}^{T}}{\left ( \sigma _{\theta }^{k} \right )^{2}}\hat{s}_{\theta }^{k}$ (12)

其中，如果轨迹是有效的，矩阵 $\sum_{k}L_{k}^{T}L_{k}$ 是可逆的；否则，问题就没有得到充分的约束。

B.其他参数的非线性估计：

我们假设 $J_{21},J_{22}$ 这两个参数已经被估计出来了，下一步就是求解参数 $\left ( b,l_{x},l_{y},l_{\theta } \right )$ 。当b是已知的时候，就可以从 $J_{21},J_{22}$ 得到 $r_{R},r_{L}$ 。

1）可处理似然近似：第一步是简化对数似然的表达式(10)。对于标准2-范数，等价关系如下：

$\left \| s^{k}-\circleddash l\oplus r^{k}\oplus l \right \|_{2}=\left \| l\oplus s^{k}-r^{k}\oplus l \right \|_{2}$

直观地说，左右两边的向量在两个不同的参照系中表示相同的量，所以它们有相同的范数。对于一般矩阵范数，这是不正确的。然而这对于 $\Sigma _{k}^{-1}$ 范数是对的。由于上面的假设1在x和y方向上是各向同性的，因此是旋转不变的。因此，(10)可以写成（这是最关键的一步，利用到假设1，这时候我们想到，假如假设1不成立怎么办，比如机器人在一个过道上，这时候机器人特征点明显呈现出方向性，假设便不成立，所以用这种方法最好是将机器人放在空旷的地方标定）：

$\jmath =-\frac{1}{2}\sum_{k}\left \| l\oplus \hat{s}^{k}-r^{k}\oplus l \right \|^{2}_{-\Sigma _{k}^{-1}}$ (13)

2）运动学积分： $r(t)=\circleddash q^{k}\oplus q(t),t\geq t_{k}$ ，自时间 $t_{k}$ 的最后一个外在观察起作为机器人的位移增量。我们需要一个 $r^{k}$ 的显式表达式作为参数的函数。 $J_{21},J_{22}$ 已知，位移可以写成参数b的线性函数。

位移 $r(t)$ 是机器人在参考坐标系的位姿，其中参考坐标系的初始值为 $r^{k}$ 。它满足这个微分方程有一个边界条件:

$\dot{r}=\left ( \begin{matrix} \dot{r}_{x}\\ \dot{r}_{y}\\ \dot{r}_{\theta } \end{matrix} \right )=\left ( \begin{matrix} vcosr_{\theta }\\ vsinr_{\theta }\\ \omega \end{matrix} \right ), r(t_{k})=0$ (13)

这个微分方程的解可以明确地写成机器人速度的函数。旋转分量 $r_{\theta }$ 的解仅仅是角速度 $\omega$ 的积分： $r_{\theta }(t)=\int_{t_{k}}^{t}\omega(\tau )d\tau$ 。因为 $\omega =J_{21}\omega _{L}+J_{22}\omega_{R}$ ，旋转分量只依赖于已知的量，因此可以估计为：

$r_{\theta }(t)=\int_{t_{k}}^{t}\left ( J_{21}\omega_{L}\left ( \tau \right ) +J_{22}\omega_{R}\left ( \tau \right )\right )d\tau$ (15)

在 $r_{\theta }(t)$ 被计算出来之后，平移部分的 $r_{x},r_{y}$ 可以写成：

$r_{x}(t)=\int_{t_{k}}^{t}v\left ( \tau \right )cosr_{\theta }\left ( \tau \right )d\tau$ (16)

$r_{y}(t)=\int_{t_{k}}^{t}v\left ( \tau \right )sinr_{\theta }\left ( \tau \right )d\tau$ (17)

带入 $v=J_{11}\omega_{L}+J_{12}\omega_{R}=b(-\frac{1}{2}J_{21}+\frac{1}{2}J_{22})$ ，最后的值可以写成一个关于b的线性函数

$r_{x}^{k}=r_{x}(t_{k+1})=c_{x}^{k}b$

$r_{y}^{k}=r_{y}(t_{k+1})=c_{y}^{k}b$

常数 $c_{x}^{k},c_{y}^{k}$ 可以表示为：

$c_{x}^{k}=\frac{1}{2}\int_{t_{k}}^{t_{k+1}}\left ( -J_{21}\omega_{L}\left ( \tau \right ) +J_{22}\omega_{R}\left ( \tau \right )\right )cosr_{\theta }^{k}\left ( \tau \right )d\tau$ (18)

$c_{y}^{k}=\frac{1}{2}\int_{t_{k}}^{t_{k+1}}\left ( -J_{21}\omega_{L}\left ( \tau \right ) +J_{22}\omega_{R}\left ( \tau \right )\right )sinr_{\theta }^{k}\left ( \tau \right )d\tau$ (19)

对于一般轨迹，需要求(15)(18)(19)的三个积分来求解 $c_{x}^{k},c_{y}^{k}$ ；但如果在区间 $t\in\left [ t_{1},t_{k+1} \right ]$ ，然后可以使用一个简化的封闭形式，如后面的第五章E节所示。

3)二次方程组：我们现在用技巧将 $cosl_{\theta }$ 和 $sinl_{\theta }$ 当作两个独立的参数。如果我们把向量 $\varphi \in R^{5}$ 中剩下的参数分组为：

$\varphi =\left ( b,l_{x},l_{y},cosl_{\theta },sinl_{\theta } \right )^{T}$

那么(13)可以写成 $\varphi$ 的二次函数。更详细的，定义一个已知系数的 $2\times 5$ 的矩阵 $Q_{k}$ ：

$Q_{k}=\frac{1}{\sigma _{xy}^{k}}\left ( \begin{matrix} -c_{x}^{k} & 1-cos\hat{r}_{\theta }^{k} & +sin\hat{r}_{\theta }^{k} &+\hat{s}_{x}^{k}-\hat{s}_{x}^{k} \\ -c_{y}^{k} & -sin\hat{r}_{\theta }^{k} & 1-cos\hat{r}_{\theta }^{k} & +\hat{s}_{y}^{k}+\hat{s}_{x}^{k} \end{matrix} \right )$ (20)

对数似然函数(13)可以简写为 $-\frac{1}{2}\varphi ^{T}M\varphi +const$ ，其中 $M=\sum_{k}Q_{k}^{T}Q_{k}$ 。我们将似然最大化问题简化为带有二次约束的二次问题：

$min \left ( \varphi ^{T}M\varphi \right )$ (21)

$s.t.\left ( \varphi _{4}^{2}+\varphi _{5}^{2}=1 \right )$ (22)

约束(22)，对应于 $cos^{2}l_{\theta }+sin^{2}l_{\theta }=1$ ，强制几何一致性是必要的。

注意，到目前为止，解还没有完全约束：如果向量 $\varphi ^{*}$ 是问题的解，那 $-\varphi ^{*}$ 也是同样可行也最优。这种现象与命题4所描述的对称性相对应。为了使问题得到充分的约束，我们添加了另一个约束 $\varphi$ 这对应于选择一个正轴b:

$\varphi _{1}\geq 0$ (23)

4）求解约束最小二乘问题:由于目标函数有下界，且可行集是封闭的，因此至少存在一个最优解。利用拉格朗日乘子法得到最优性条件。约束(22)以矩阵形式表示为：

$\varphi ^{T}W\varphi =1,W=\left (\begin{matrix} 0_{3\times3} &0_{3\times2} \\ 0_{2\times3} & I_{2\times2} \end{matrix}\right )$ (24)

考虑到拉格朗日算子 $\L =\varphi ^{T}M\varphi +\lambda \left ( \varphi ^{T}W\varphi -1\right )$ 。在这个问题中，斯莱特的条件成立，因此Karush–
Kuhn–Tucker（KKT）条件是最优的必要条件：

$\frac{\partial \L ^{T}}{\partial x}=2\left ( M+\lambda W \right )\varphi =0$ (25)

式(25)表示需要找到一个 $\lambda$ 使得矩阵 $M+\lambda W$ 是奇异矩阵，然后在这个矩阵的核中找到求解 $\varphi$ 。 $\lambda$ 的值可以通过求解方程 $det(M+\lambda W)=0$ 解方程得到。

对任意一个M, $det(M+\lambda W)=0$ 的表达式对于 $\lambda$ 来说都是个五次多项式。然而，由于 $Q_{k}$ 的重复输入，这个多项式对矩阵 $M=\sum _{k}Q_{k}^{T}Q_{k}$ 来说只是二阶的。可以看出M的结构如下(注意0和重复项)：

$M=\left [ \begin{matrix} m_{11} & 0 & m_{13} & m_{14} & m_{15}\\ & m_{22} & 0 & m_{35} & -m_{34}\\ & & m_{22} & m_{34} & m_{35}\\ & & & m_{44}& 0\\ (symmetric)& & & &m_{44} \end{matrix} \right ]$

$M+\lambda W$ 的行列式是一个二阶多项式 $a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}$ ，其中系数值如下所示：

$\lambda$ 两个候选解可以用封闭形式求二阶多项式的根；应该检查两个候选解，计算相应的向量，并检查哪一个对应于问题的最小值(21)。

假设 $\lambda ^{(i)},i=1,2$ 是两个候选解中的一个。通过构建， $5\times5$ 的矩阵 $M+\lambda W$ 的秩最多为4。在前面讨论的兴奋性条件下，秩保证恰好为4。事实上，除此之外我们将能够找到 $\varphi$ 的连续解，因为可观测性分析保证了解的局部唯一性。

如果秩为4，那么内核的维度为1，并且在给定约束(9)和(23)的情况下， $\varphi$ 的选择是惟一的。假设 $\gamma ^{(i)}成为$ 是 $M+\lambda^{(i)} W$ 的核中的任意非零向量。为了能得到解 $\varphi ^{(i)}$ ，将 $\gamma ^{(i)}成为$ 按 $\sqrt{\left ( \gamma _{4}^{(i)} \right )^{2}+ \left( \gamma _{5}^{(i)} \right )^{2} }$ 进行缩放以强制约束(9)，然后将其翻转到 $\gamma ^{(i)}成为$ 的符号以满足约束(23)：

$\varphi ^{(i)}=\frac{sign(\gamma _{1}^{(i)})}{\sqrt{\left ( \gamma _{4}^{(i)} \right )^{2}+\left ( \gamma _{5}^{(i)} \right )^{2}}}\gamma ^{(i)}$ (29)

通过计算目标函数的值，根据（21）正确的求解结果 $\hat{\varphi }$ 可以在 $\varphi ^{(1)}$ 和 $\varphi ^{(2)}$ 之间被选择出来。之后便可以对所有六个参数进行恢复求解：

$\left\{\begin{matrix} \hat{b}=\hat{\varphi }_{1}\\ \hat{r}_{L}=-\hat{\varphi _{1}}\hat{J}_{21}\\ \hat{r}_{R}=+\hat{\varphi _{1}}\hat{J}_{22}\\ \hat{l}=\left ( \hat{\varphi }_{2}, \hat{\varphi }_{3},arctan2(\hat{\varphi }_{5},\hat{\varphi }_{4},)\right ) \end{matrix}\right.$ (30)

C.离群点移除

我们的方法的实用性来自于这样一个事实，一个人可以很容易地获得数以千计的观察，通过驾驶机器人，无人看管，沿着任意的轨迹(比较，例如，与博伦斯坦的方法，这是基于精确观察一小组数据)。不幸的是，在成千上万的观测数据中，很可能有一些是无法使用的，这是由于车轮打滑、传感器位移估计程序失败以及传感器和里程表观测数据的不正确同步造成的。从理论上讲，一个孤立点可以使估计值任意远离真实值；通常，最大似然估计量的击穿点为0。因此，该算法的一个整体部分是异常值去除过程，它包含在经典的策略中，逐步丢弃看起来不一致的[30]样本的一部分。

将样本称为相对于第k个间隔的一组测量值(车轮速度、估计的传感器位移)。样本之间是相互独立处理的，异常值删除过程包括删除那些看起来异常值的样本，如下所示。

重复N次：

1）用当前样本运行校准程序。

2）计算每个样本的 $\chi$ 值，用下述表达式（经典的卡方分布）：

$\chi ^{k}=\left \| \hat{s}^{k}-\circleddash \hat{l}\oplus r^{k}\left ( \hat{r}_{L},\hat{r}_{R},\hat{b} \right ) \oplus \hat{l}\right \|_{\Sigma _{k}^{-1}}$ (31)

3）丢弃 $\chi$ 值最大的样本的一小部分 $\alpha$ 。

当然，参数n和 $\alpha$ 取决于数据的属性。

在实施该方法时，考察了残差的经验分布：

$e^{k}=\hat{s}^{k}-\circleddash \hat{l}\oplus r^{k}\left ( \hat{r}_{L},\hat{r}_{R},\hat{b} \right )\oplus \hat{l}$ (32)

给出了关于估计过程收敛性的宝贵信息。理想情况下，如果估算准确， $e^{k}$ 应根据传感器位移估计程序的误差模型进行分布。例如，图3显示了稍后将展示的一个实验中残差的演变。我们可以看到，在第一次迭代中(图3a)有几个异常值;随着每次迭代，较大的离群点被丢弃，由于估计的改进，残差分布趋于高斯分布(图3b)，其中x,y的误差为毫米级， $\theta$ 误差在1度以下。

图3.残差分布。该方法的一个组成部分是识别和去除异常值，这些异常值可能是由于车轮打滑、传感器位移估计过程中的故障以及其他未建模的噪声源造成的。为了识别异常值，首先进行校准，然后根据式(32)计算每个样本的残差。将残差较大的样品丢弃，重复该过程。残差的分布提供了关于估计质量的信息。(a):在第一次迭代中，我们期望有较大的残差。如果过程是正确的，残差最终应该根据传感器模型分布。(b):在这种情况下，我们看到在校准结束时，残差是按照扫描匹配误差过程分布的:近似高斯分布，精度为毫米和度的分数。

D.不确定度估计

我们利用克拉美罗界来估计解的不确定性。回想一下，CRB是可获得的估计精度的下限。结果表明，最大似然估计量是渐近无偏的，达到了CRB[28]。如果我们有成千上万个样本，我们期望处于最大似然估计的渐近状态。

CRB是由费雪信息矩阵(FIM)的逆计算得到的，它依赖于观测模型和观测噪声。假设有这样一个模型 $y_{k}=f_{k}(x)+\epsilon _{k}$ ，其中函数f是可微的。x是个n维向量，y是个m维向量， $\epsilon _{k}$ 是一个方差为 $\sigma _{k}$ 的高斯噪声。FIM是一个 $n \times n$ 矩阵，由这个式子定义： $I(x)=\sum_{k}\frac{\partial f_{k}}{\partial x}\Sigma _{k}^{-1}\frac{\partial f_{k}}{\partial x}$ 。在某些技术条件[28]下，CRB声明任何x的无偏估计量 $\hat{x}$ 都有界： $cov(\hat{x})\geq I(x)^{-1}$ 。在我们的例子中，观察值是 $y_{k}=\hat{s}^{k}$ ，状态值是 $x=\left ( r_{R},r_{L},b,l_{x},l_{y},l_{\theta } \right )$ 并且观测模型 $f_{k}$ 由（9）定义，这个和观测 $\frac{\partial f_{k}}{\partial x}$ 不同。

E.车轮速度常数的简单公式

在V-A节和V-B节中，我们需要对运动学进行积分，从而得到优化问题中的一些系数。如果车轮速度在时间 $t\in\left [ t_{1},t_{k+1} \right ]$ 间隔内是恒定的，公式可以简化。

如果机器人速度是常数（这又是一个强假设，实际上机器人运行过程中起停往往比较频繁，所以在标定过程中最好流畅地一趟完成），即 $v(t)=v_{0},\omega(t)=\omega_{0}\neq 0$ ，微分方程（14）的解为：

$r(t)=\left ( \begin{matrix} \frac{v_{0}sin(\omega_{o}t)}{\omega_{0}}\\ \frac{v_{0}(1-cos(\omega_{0}t))}{\omega_{0}}\\ \omega_{0}t \end{matrix} \right )$ (33)

有关证明，请参阅例如[31,p. 516，公式(11.85)]。假设 $\omega_{L}^{k},\omega_{R}^{k}$ 是车轮在时间间隔 $t\in\left [ t_{1},t_{k+1} \right ]$ 运行的常速度，用公式（33），公式（11）可以简化为：

$L_{k}=\left ( T^{k}\omega_{L}^{k},T^{k}\omega_{R}^{k} \right )$ (34)

公式(18)-(19)化简为：

$r_{\theta }^{k}=J_{21}T^{k}\omega_{L}^{k}+J_{22}T^{k}\omega_{R}^{k}$ (35)

$c_{x}^{k}=\frac{1}{2}T^{k}\left ( -J_{21}\omega_{L}^{k}+J_{22}\omega_{R}^{k} \right )\frac{sin\left ( r_{\theta }^{k} \right )}{r_{\theta }^{k}}$ (36)

$c_{y}^{k}=\frac{1}{2}T^{k}\left ( -J_{21}\omega_{L}^{k}+J_{22}\omega_{R}^{k} \right )\frac{1-cos\left ( r_{\theta }^{k} \right )}{r_{\theta }^{k}}$ (37)

因此，如果速度在每个区间都是常数，就不需要对任何积分进行数值计算。

六、实验

我们使用Khepera III机器人和机载Hokuyo URG-04LX测距仪测试了该方法。实验数据和使用的软件作为补充材料的一部分。

A.启动

1）机器人:Khepera III是一款适合教育用途的小型移动机器人(图2)，直径13 cm，重量690 g。无刷伺服电机允许最大速度0.5米/秒。Khepera III的编码器分辨率约为每度7个数。Khepera上的CPU比较老 (DsPIC 30 f5011 60 MhZ专有Korebot扩展在400 MhZ)，太慢执行实时扫描匹配，因为它不具备一个浮点单元：在桌面计算机上，扫描匹配操作大约需要10 ms，而在Khepera上，使用浮点模拟大约需要10 s。因此，测距仪和里程表测量数据被传送回运行校准程序的台式计算机。考虑到扫描匹配结果 $\hat{s}^{k}$ ，校准算法本身的计算成本可以忽略不计，并且可以在Khepera上实现，甚至可以使用浮点仿真。

2）传感器：Hokuyo URG-04LX是一款小型轻量级测距传感器[32]、[33]。它提供了超过240度视场的681条光线，径向分辨率为1毫米，标准偏差约为3毫米。测量结果高度相关，每条射线的误差都与其3-4邻边相关：这可能是某种后处理(插值)的症状，目的是将分辨率提高到名义上的1024/360射线/度。有一种偏差显示出时间漂移:读数在5分钟内变化多达20毫米，这可能是由于电池电量或温度的变化。此外，还存在空间偏差，这是距离[32]的函数:在实际中，矩形环境对传感器来说略呈弯曲。尽管存在这些问题，我们估计扫描匹配操作的结果在小位移(5-10厘米)情况下，精度为1mm和十分之一度。

图2.实验中使用的Khepera III机器人带有机载的Hokuyo URG-04LX测距仪

3）传感器位移估计:为了得到估计的 $\hat{s}^{k}$ ，我们使用了[34]中描述的扫描匹配方法。

估计协方差 $\Sigma _{k}$ 的方法有很多种：或者使用扫描匹配方法的内部工作原理知识(如[35])，或者使用与算法无关的类crb边界[36]，但假设知道外部感受传感器的分析模型。

或者，如果机器人一直在一个均匀的环境中收集测量值（均匀的环境很关键），那么通过一个常数矩阵 $\Sigma$ 近似协方差 $\Sigma _{k}$ 是合理的。这个常数矩阵 $\Sigma$ 可以使用更简单(和更健壮)的方法从数据中计算 $e^{k}$ 的协方差进行标识，在得到解之后。

4）构型:为了测试该方法，我们在机器人上尝试了三种构型的激光位姿。这允许检查里程表参数的估计值是否与激光器的不同配置保持一致。我们标记了三种构型A、B、C。

5）轨迹:该方法允许使用任何轨迹，只要充分激发所有参数即可。实际考虑建议：

i.在一个小的密闭空间中产生闭合轨迹的输入，这样机器人就可以在无人看管的情况下运行。

ii. 选择分段常数输入。这允许使用V-E节中的简化公式，并且在一个区间内只记住 $\omega_{L}$ 和 $\omega_{R}$ 的一个值，而不是记住整个概要文件 $\omega_{L}(t),\omega_{R}(t)$ ， $t\in\left [ t_{1},t_{k+1} \right ]$ ，这是对一般情况使用公式所必需的。

在实验中，我们根据包含四对“规范”输入的轨迹驱动机器人：

$\left ( \omega_{L},\omega_{R} \right )=\pm c\left ( +1,+1 \right )$ （直行）

$\left ( \omega_{L},\omega_{R} \right )=\pm c\left ( +1,-1 \right )$ （顺时针原地旋转）

$\left ( \omega_{L},\omega_{R} \right )=\pm c\left ( +1,0 \right )$ （右转弯）

$\left ( \omega_{L},\omega_{R} \right )=\pm c\left ( 0,+1 \right )$ （左转弯）

与这些输入相关联的标称轨迹是基本的。特别是，第一个输入对应一条直线轨迹；二是机器人原地转弯；最后两种运动是由只移动一个轮子引起的。这些轨迹被拼接在一起，这样，在每次执行结束时，机器人返回到起始姿势(向上漂移);这样，校准程序就有可能在一个密闭的空间中无人值守地运行。

B.数值结果

对于每个配置A、B、C，我们使用前面提到的输入收集了几个数据日志。然后，我们将每个配置的数据细分为三个子集，分别命名为A1、A2、A3、B1、B2等。每个子集总共由3500个测量样本组成。

对于每个配置，我们对完整的数据集以及每个子集单独运行校准算法。考虑相同配置的多个子集可以检查不确定度估计是否一致：例如，我们期望子集A1和A2给出的校准结果略有不同，但这些结果必须不超过估计的置信限预测。

参数的标定结果如图4所示。子图4a 4f显示了对参数的估计 $r_{R},r_{L},b,l_{x},l_{y},l_{\theta }$ 。图4 - 4j显示了相同的参数 $J_{11},J_{12},J_{21},J_{22}$ 。误差条对应于的置信值 $3\sigma$ 给出了计算克拉默劳界的方法。相同的数据以文本形式显示在表II中。

图4.校正后的参数及置信区间(相同的资料以表格形式列于表II)。对于每一组态，分别取三个对数(例如A1、A2、A3)，并一并考虑(“A”)。因此，我们总共有12个数据集。在x轴上我们找到了实验标签;在y轴上，估计值随着3o置信中心。置信条对应于由crmer - rao界计算的绝对可达到的精度，如V-D节所述。注意，大多数变量高度相关，因此只绘制标准差可能会误导;相关信息见图5。

图5.估计误差之间的相关模式。图4为每个变量的3o误差置信带。这就相当于只考虑协方差矩阵的对角元素，而忽略了相关信息。事实证明，每个配置都有一个典型的相关模式，它严格地描述了总体精度。子图(a)、(b)、(c)显示了三种配置的相关模式。网格中的每个单元格包含坐标轴上的两个变量之间的相关性。

该方法的精度在毫米和十分之一度的顺序为激光的姿态，这是不可能为我们测量地面真相这样的精度。然而，我们可以使用间接验证声称性能非常接近于最优:通过处理相同日志的不同子集，并验证结果与关联的Cramer Rao边界给出的置信级别一致。例如，在图4中，我们看到，虽然 $r_{L}$ 的估计值在A1、A2、A3集合中是不同的，但是它们与置信限是相容的。用同样的方法，我们可以比较每一种配置的 $l_{x},l_{y},l_{\theta }$ 的估计值。

此外，对测程参数 $r_{R},r_{L},b$ （以及等价参数化 $J_{11},J_{12},J_{21},J_{22}$ ）进行了估计也可以比较所有三种构型A, B, C。例如，在图4g-4j中，我们可以看到，虽然 $J_{11},J_{12},J_{21},J_{22}$ 的估计值在每个集合中都发生了变化，而且不确定性也有很大的变化，但是所有的数据都与克拉美多界给出的置信度是一致的。

注意,不确定性(误差)有明显的不同配置,即使测量的数量是每组大致相同。为了解释这个明显的矛盾,每个人都应该记得,信心限制为单个变量只给出部分的估计精度；实际上，它等价于只考虑协方差矩阵的对角项，而忽略了变量之间的相关信息。例如，对 $r_{L}$ 和b的估计是强正相关的，因为是它们的比值 $J_{21}=r_{L}/b$ 是直接可观的。

在这种情况下，各变量之间存在较大的相关性，且相关性受传感器位姿配置的影响。如图5所示，其中给出了各变量之间的相关模式。在图5b中，我们可以看到位移传感器引入了之间的强相关性在 $l_{x},l_{y},l_{\theta }$ 之间。对比图5a和图5c，我们可以看到，仅仅旋转传感器并不会改变相关模式。

七、结论

本文提出了一种简单实用的同时标定差动驱动机器人的里程表参数和安装在机器人上的外感受传感器的外位姿的方法。该方法有一些有趣的特点:它可以在无人看管的情况下运行，无需人工干预;没有任何仪器需要预先校准;不需要标称参数作为初始猜测，全局最优解以封闭形式存在;机器人的轨迹可以自由选择，只要它们激活所有的参数。我们有实验评价方法在移动平台上配备了激光测距仪放置在各种配置,使用扫描匹配作为传感器位移估计方法,我们已经表明,校准精度与理论极限的Cramér Rao bound。

在这项工作可能的发展中，我们提到了其他移动平台的运动学模型的同时标定问题，例如轮式机器人。另一个有趣的扩展是将问题转移到动态设置中，使用一个测量力或加速度的传感器。

参考文献：

[1] J. Doebbler, J. Davis, J. Junkins, and J. Valasek, “Odometry and calibration methods for multi-castor vehicles,” in Proceedings of the IEEE International Conference on Robotics and Automation, pp. 2110–
2115, May 2008.

[2]J. Von der Hardt, R. Husson, and D. Wolf, “An automatic calibration method for a multisensor system: application to a mobile robot localization system,” in Proceedings of the IEEE International Conference on Robotics and Automation, vol. 4, (Leuven, Belgium), pp. 3141–3146, May 1998.

[3] J. Borenstein and L. Feng, “Measurement and correction of systematic odometry errors in mobile robots,” IEEE Transactions on Robotics and Automation, vol. 12, December 1996.

[4] A. Kelly, “Fast and easy systematic and stochastic odometry calibration,” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, vol. 4, pp. 3188–3194, Sept./Oct. 2004.

[5] T. D. Larsen, M. Bak, N. A. Andersen, and O. Ravn, “Location estimation for an autonomously guided vehicle using an augmented Kalman filter to autocalibrate the odometry,” in First International Conference on Multisource-Multisensor Information Fusion (FUSION’98), 1998.

[6] D. Caltabiano, G. Muscato, and F. Russo, “Localization and selfcalibration of a robot for volcano exploration,” in Proceedings of the IEEE International Conference on Robotics and Automation, vol. 1,
pp. 586–591, Apr./May 2004.

[7] A. Martinelli, N. Tomatis, and R. Siegwart, “Simultaneous localization and odometry self calibration for mobile robot,” Autonomous Robots, vol. 22, pp. 75–85, 2006.
[8] E. Foxlin, “Generalized architecture for simultaneous localization, autocalibration, and map-building,” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, vol. 1, pp. 527–533 vol.1, 2002.
[9] N. Roy and S. Thrun, “Online self-calibration for mobile robots,” in Proceedings of the IEEE International Conference on Robotics and Automation, 1999.
[10] G. Antonelli, S. Chiaverini, and G. Fusco, “A calibration method for odometry of mobile robots based on the least-squares technique: theory and experimental validation,” IEEE Transactions on Robotics, vol. 21, pp. 994–1004, Oct. 2005.
[11] G. Antonelli and S. Chiaverini, “Linear estimation of the physical odometric parameters for differential-drive mobile robots,” Autonomous Robots, vol. 23, no. 1, pp. 59–68, 2007.
[12] G. Antonelli and S. Chiaverini, “A deterministic filter for simultaneous localization and odometry calibration of differential-drive mobile robots,” in Third European Conference on Mobile Robots, 2007.
[13] Q. Zhang and R. Pless, “Extrinsic calibration of a camera and laser range finder (improves camera calibration),” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, vol. 3, pp. 2301–2306, 2004.
[14] X. Brun and F. Goulette, “Modeling and calibration of coupled fisheye ccd camera and laser range scanner for outdoor environment reconstruction,” in 3DIM07, pp. 320–327, 2007.

[15] H. Aliakbarpour, P. Nuez, J. Prado, K. Khoshhal, and J. Dias, “An efficient algorithm for extrinsic calibration between a 3d laser range finder and a stereo camera for surveillance,” in International Conference on Advanced Robotics (ICAR), pp. 1–6, June 2009.
[16] A. Martinelli and D. Scaramuzza, “Automatic self-calibration of a vision system during robot motion,” in Proceedings of the IEEE International Conference on Robotics and Automation, (Orlando, Florida), 2006.
[17] A. Martinelli and R. Siegwart, “Observability properties and optimal trajectories for on-line odometry self-calibration,” in 45th IEEE Conference on Decision and Control, pp. 3065–3070, Dec. 2006.
[18] F. Mirzaei and S. Roumeliotis, “A kalman filter-based algorithm for imucamera calibration: Observability analysis and performance evaluation,” IEEE Transactions on Robotics, vol. 24, pp. 1143–1156, Oct. 2008.
[19] J. Hesch, A. Mourikis, and S. Roumeliotis, “Determining the camera to robot-body transformation from planar mirror reflections,” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 3865–3871, Sept. 2008.
[20] J. P. Underwood, A. Hill, T. Peynot, and S. J. Scheding, “Error modeling and calibration of exteroceptive sensors for accurate mapping applications,” Journal of Field Robotics, vol. 27, pp. 2–20, Jan. 2010.
[21] J. Brookshire and S. Teller, “Automatic Calibration of Multiple Coplanar Sensors,” in Proceedings of Robotics: Science and Systems (RSS), 2011. [22] A. Censi, L. Marchionni, and G. Oriolo, “Simultaneous maximumlikelihood calibration of robot and sensor parameters,” in Proceedings
of the IEEE International Conference on Robotics and Automation, (Pasadena, CA), May 2008.
[23] A. Martinelli, “Local decomposition and observability properties for automatic calibration in mobile robotics,” in Proceedings of the IEEE International Conference on Robotics and Automation, pp. 4182–4188, May 2009.
[24] A. Martinelli, “State Estimation Based on the Concept of Continuous Symmetry and Observability Analysis: The Case of Calibration,” IEEE Transactions on Robotics, vol. 27, no. 2, pp. 239–255, 2011.
[25] G. Antonelli, F. Caccavale, F. Grossi, and A. Marino, “A non-iterative and effective procedure for simultaneous odometry and camera calibration for a differential drive mobile robot based on the singular value decomposition,” Intelligent Service Robotics, vol. 3, pp. 163–173, June 2010.
[26] R. M. Murray, Z. Li, and S. S. Sastry, A Mathematical Introduction to Robotic Manipulation. CRC, 1 ed., March 1994.
[27] R. Hermann and A. Krener, “Nonlinear controllability and observability,” IEEE Transactions on Automatic Control, vol. 22, pp. 728–740, Oct 1977.
[28] H. L. V. Trees and K. L. Bell, Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking. Wiley-IEEE Press, 2007.
[29] S. Boyd and L. Vandenberghe, Convex Optimization. New York, NY, USA: Cambridge University Press, 2004.

[30] P. J. Rousseeuw and A. M. Leroy, Robust regression and outlier detection (3rd edition). John Wiley & Sons, 1996.
[31] B. Siciliano, L. Villani, L. Sciavicco, and G. Oriolo, Robotics: Modelling, Planning and Control. Springer, 2008.
[32] H. Kawata, A. Ohya, S. Yuta, W. Santosh, and T. Mori, “Development of ultra-small lightweight optical range sensor system,” in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 1078–1083, Aug. 2005.
[33] L. Kneip, F. T. G. Caprari, and R. Siegwart, “Characterization of the compact hokuyo URG-04LX 2d laser range scanner,” in Proceedings of the IEEE International Conference on Robotics and Automation, (Kobe, Japan), 2009.
[34] A. Censi, “An ICP variant using a point-to-line metric,” in Proceedings of the IEEE International Conference on Robotics and Automation, pp. 19–25, May 2008. Source code available at http://andreacensi.github. com/csm/. Also available as a ROS package at http://www.ros.org/wiki/
laser_scan_matcher.
[35] A. Censi, “An accurate closed-form estimate of ICP’s covariance,” in Proceedings of the IEEE International Conference on Robotics and Automation, (Rome, Italy), pp. 3167–3172, Apr. 2007.
[36] A. Censi, “On achievable accuracy for pose tracking,” in Proceedings of the IEEE International Conference on Robotics and Automation, (Kobe, Japan), pp. 1–7, May 2009.

hello我是小菜鸡

关注

8
点赞
踩
50

收藏

觉得还不错? 一键收藏
5
评论
同时校准移动机器人的里程表和传感器参数

Simultaneous calibration of odometry and sensor parameters for mobile robots，Andrea Censi, Student Member, Antonio Franchi, Member, Luca Marchionni, and Giuseppe Oriolo, Senior Member，2013，IEEE Trans...
复制链接

扫一扫