滤波笔记一：卡尔曼滤波

Reference:

1. 轻松理解卡尔曼滤波

1. Overview

• 滤波前提:
  数据满足高斯分布。
• 通俗解释:
  假设知道两个传感器，其中贵的那个传感器准一些，便宜的那个差一些，则比取平均更好的方法为：加权平均
  
  怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的均值和方差值，你就可以得到一个“最优”的权重。
  
  假设只有一个传感器，但还有一个数学模型。模型可以帮你算出一个值，但是也不那么准。可以把模型算出来的值，和传感器测出来的值，取加权平均。

2. 应用场景

假设开发了一款小型的机器人，它可以在树林里自主移动，并且这款机器人需要明确自己的位置以便进行导航。我们可以通过一组状态变量来描述机器人的状态，包括位置和速度：
$$\overrightarrow{x_k}=(\vec{p},\vec{v})$$注意这个状态仅仅是系统所有状态中的一部分，你可以获取任何数据变量作为观测的状态，在我们这个例子中，所选取的是位置和速度。但是，它也可以是水箱中的水位，汽车引擎的温度，或者任何你想要跟踪的数据。

1.我们的机器人拥有一个 GPS 传感器，精度在 10m。这已经很好了，但是对于机器人来说，它需要以远高于 10m 的精度来定位自己的位置。在机器人所处的树林里有很多溪谷和断崖，如果机器人对位置误判了哪怕几步远的距离，它就有可能掉到坑里。所以仅靠 GPS 是不够的。

2.同时，我们可以获取到一些机器人的运动信息：驱动轮子的电机指令对我们也有用处。如果没有外界干扰，仅仅是朝一个方向前进，那么下一时刻的位置只是比上一时刻的位置在该方向上移动了一个固定的距离。当然我们无法获取影响运动的所有信息：机器人可能会收到风力影响，轮子可能会打滑，或者碰到了一些特殊的情况等等。所以轮子转过的距离并不能完全表示机器人移动的距离，这就导致通过轮子转动预测机器人位置不会非常准确。

3.如何综合两者的信息获得比单独信息来源更精确的结果，这就是卡尔曼滤波要解决的问题。

3. 变量定义

• $x$: 平均状态向量(state vector)。对于一个扩展卡尔曼滤波器，平均状态向量包含关于所跟踪的物体的位置和速度的信息。它被称为“平均”状态向量，因为位置和速度是用均值 $x$ 表示的高斯分布。
• $P$: 状态协方差矩阵(state incertainty)，包含了物体位置和速度的不确定性信息。
• $R$: 测量噪声协方差矩阵(Measurement noise convariance matrix)，测量带来的噪声。
• $Q$: 系统噪声协方差矩阵(System noise convariance matrix)，外界有很多影响因素，如有时会有顺风，有时则是逆风。
• $u$: 外部运动，如施加的外力等。
• $F$: 状态传递矩阵(Transition matrix)。
• $H$: 测量矩阵(Measurement matrix)。
• $k$: 时间步长，所以 $x_k$ 指的是 $k$ 时刻物体的位置和速度矢量。
• 符号 $k+1|k$ 代表预测阶段。如 $x_{k+1|k}$ 意味着已经预测了物体在 $k+1$ 时间会在哪，但还没有将传感器测量考虑进去。
• $x_{k+1}$: 已经预测了物体在 $k+1$ 时间的位置，并且已使用传感器测量来更新物体的位置和速度。
• $K$: 卡尔曼增益(Kalman gain)。

4. 如何看待卡尔曼滤波问题

$$\vec{x}=\left[\begin{array}{l}p\\ v\end{array}\right]$$

我们不知道位置和速度的准确值，但是我们可以列出一个准确数值可能落在的区间。在这个范围里，一些数值的组合的可能性要高于另一些组合的可能性，如下图左。

卡尔曼滤波假设所有的变量是随机的且符合高斯分布（正态分布）。每一个变量有一个平均值 $\mu$，代表了随机分布的中心值（也表示这是可能性最大的值），和一个方差 ${\sigma }^2$，代表了不确定度，如下图右。

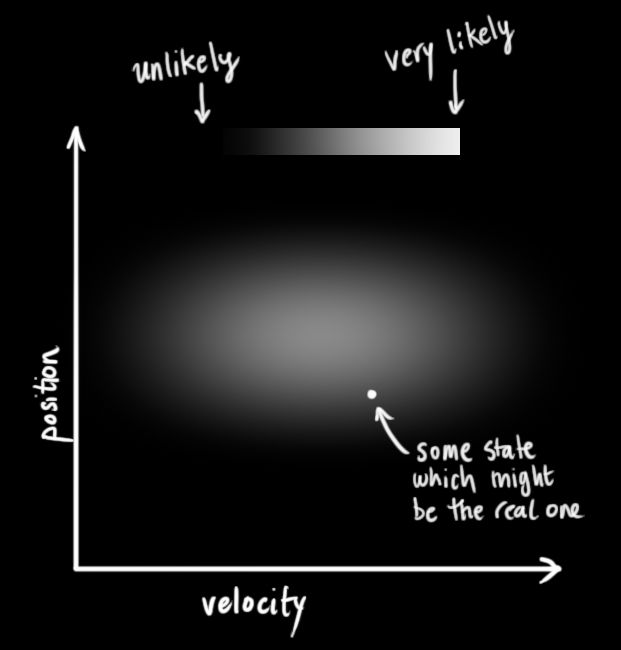
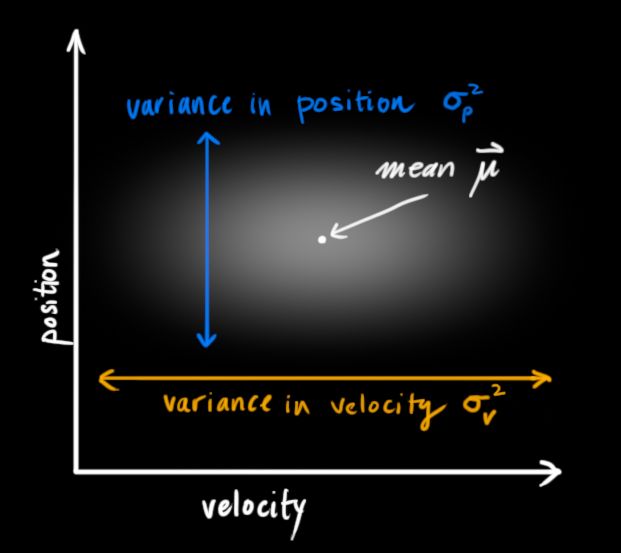
上图中位置和速度是无关联的，即系统状态中的一个变量并不会告诉你关于另一个变量的任何信息。下图左则展示了一些有趣的事情：在现实中，速度和位置是有关联的。如果已经确定位置的值，那么某些速度值存在的可能性更高。

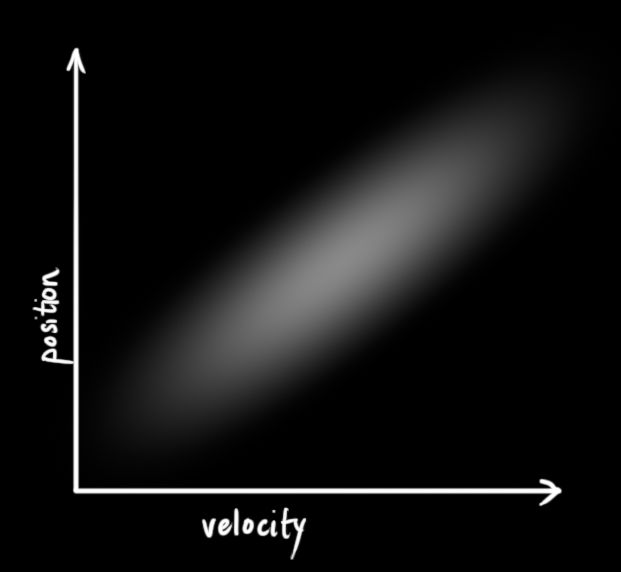
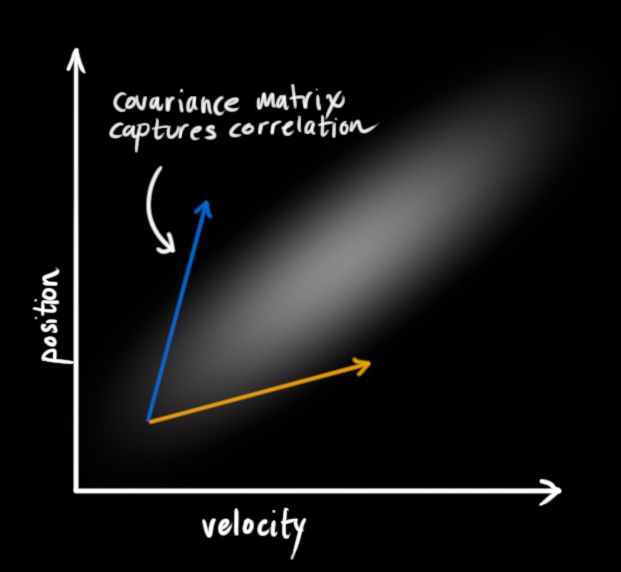
假如我们已知上一个状态的位置值，现在要预测下一个状态的位置值。如果我们的速度值很高，我们移动的距离会远一点。相反，如果速度很慢，机器人不会走的很远。
这种关系在跟踪系统状态时很重要，因为它给了我们更多的信息：一个测量值告诉我们另一个测量值可能是什么样子。这就是卡尔曼滤波的目的，我们要尽量从所有不确定信息中提取有价值的信息。

这种关系可以通过一个称作协方差的矩阵表述。简而言之，矩阵中的每个元素 ${\Sigma }_{ij}$ 表示了第 $i$ 个状态变量和第 $j$ 个状态变量之间的关系（也就是说协方差矩阵是对称的，即交换下标 $i$ 和 $j$ 并无任何影响）。协方差矩阵通常表示为 $\Sigma$，它的元素则表示为 ${\Sigma }_{ij}$。
$${\Sigma }_{ij}=\mathrm{Cov}\left(x_i,x_j\right)=E\left[\left(x_i-{\mu }_i\right)\left(x_j-{\mu }_j\right)\right]$$

4.1 利用矩阵描述问题

我们对系统状态的分布建模为高斯分布，所以在 $k$ 时刻我们需要两个信息：最佳预估值 ${\bar{x}}_k$（平均值），和它的协方差矩阵 $P_k$：
$${\hat{\mathbf{x}}}_k=\left[\begin{array}{l}\text{ position }\\ \text{ velocity }\end{array}\right],{\mathbf{P}}_k=\left[\begin{array}{ll}{\Sigma }_{pp}& {\Sigma }_{pv}\\ {\Sigma }_{vp}& {\Sigma }_{vv}\end{array}\right]$$这里我们只记录了位置和速度，但是我们可以把任何数据变量放进我们的系统状态里。

下一步，我们需要通过 $k-1$ 时刻的状态来预测 $k$ 时刻的状态。请注意，我们不知道状态的准确值，但是我们的预测函数并不在乎。它仅仅是对 $k-1$ 时刻所有可能值的范围进行预测转移，然后得出一个 $k$ 时刻新值的范围，如下左图所示：

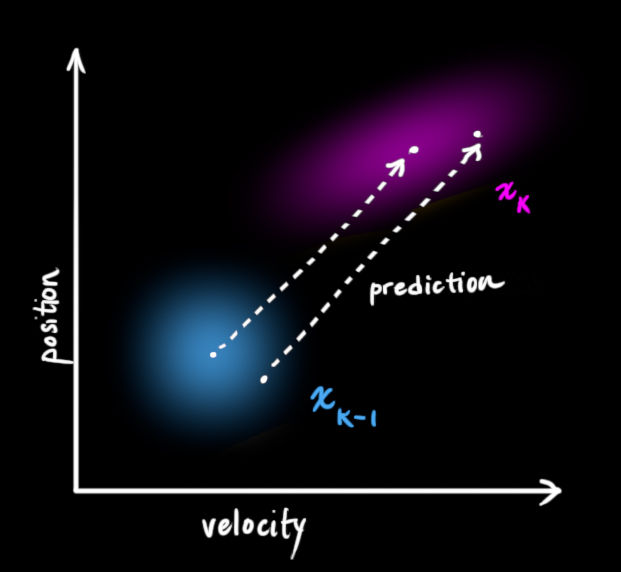
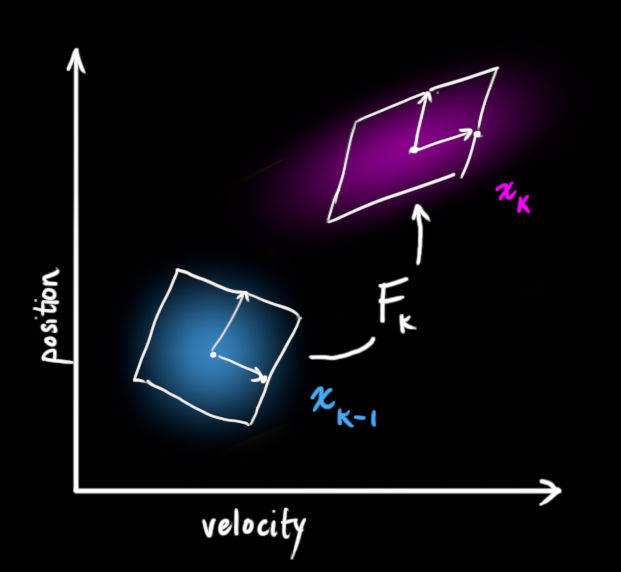
我们可以通过一个状态转移矩阵 $F_k$ 来描述这个变换，如上右图所示。把 $k-1$ 时刻所有可能的状态值转移到一个新的范围内，这个新的范围代表了系统新的状态值可能存在的范围，如果 $k-1$ 时刻的估计值范围是准确的话，如上右图所示：

通过一个运动公式来表示这种预测下一个状态的过程：
$$\begin{array}{lr}{p}_k=p_{k-1}+& \Delta t{v}_{k-1}\\ v_k=& v_{k-1}\end{array}$$整理，得矩阵：
$$\begin{array}{rl}{\hat{\mathbf{x}}}_k& =\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]{\hat{\mathbf{x}}}_{k-1}\\ & ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}\end{array}$$我们现在有了一个状态转移矩阵，可以简单预测下一个状态，但仍不知道如何更新协方差矩阵。

这里我们需要知道一个公式，如果我们对每个点进行矩阵A转换，它的协方差矩阵$\Sigma$会发生的变化为：
$$\begin{array}{rl}\mathrm{Cov}(x)& =\Sigma \\ \mathrm{Cov}(\mathbf{A}x)& =\mathbf{A}\Sigma {\mathbf{A}}^T\end{array}$$结合之前的式子可得：
$$\begin{array}{l}{\hat{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}\\ {\mathbf{P}}_k={\mathbf{F}}_{\mathbf{k}}{\mathbf{P}}_{k-1}{\mathbf{F}}_k^T\end{array}$$可知状态协方差矩阵为什么是以 $P^{\prime }=FP{F}^T$ 更新的。

4.2 外界作用力

这时的系统并没有考虑到所有影响因素。系统状态的改变并不止依靠上一个状态系统，外界作用力可能会影响系统状态的变化。

例如，跟踪一列火车的运动状态，火车驾驶员可能踩了油门使火车提速。同样，在我们机器人例子中，导航软件可能发出一些指令启动或者制动轮子。如果我们知道这些额外的信息，我们可以通过一个向量 $\overline{u_k}$ 来描述这些信息，把它添加到我们的预测方程里作为一个修正。

假如我们通过发出的指令得到预期的加速度 $a$，上面的运动方程可以变化为：
$$\begin{array}{ll}{p}_k=p_{k-1}+& \Delta t{v}_{k-1}+\frac{1}{2}a\Delta t^2\\ v_k=& v_{k-1}+a\Delta t\end{array}$$矩阵形式可以写为：
$$\begin{array}{rl}{\hat{\mathbf{x}}}_k& ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+\left[\begin{array}{c}\frac{\Delta t^2}{2}\\ \Delta t\end{array}\right]a\\ & ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k\overrightarrow{{\mathbf{u}}_k}\end{array}$$$B_k$ 称作控制矩阵，$\overrightarrow{u_k}$ 称作控制向量（如果没有任何外界动力影响的系统，可以忽略该项）。

4.3 外界不确定性

如果状态只会根据系统自身特性演变那将不会有任何问题。

但是会出现一些外力无法预测的情况：假如我们在跟踪一个四轴飞行器，它会受到风力的影响。如果我们在跟踪一个轮式机器人，轮子可能会打滑，或者地面上的凸起会使它降速。我们无法跟踪这些因素，并且这些事情发生的时候上述的预测方程可能会失灵。这时候，需要在预测方程中添加一个不确定项-----这样，原始状态中的每一个点都可以预测转换到一个范围，而不是某个确定的点。可以这样描述：${\bar{x}}_{k-1}$ 中的每个点移动到一个符合方差 $Q_k$ 的高斯分布里。另一种说法，我们把这些不确定因素描述为方差为 $Q_k$ 的高斯噪声。

如下右图所示，这样会产生一个新的高斯分布，方差不同，但是均值相同。

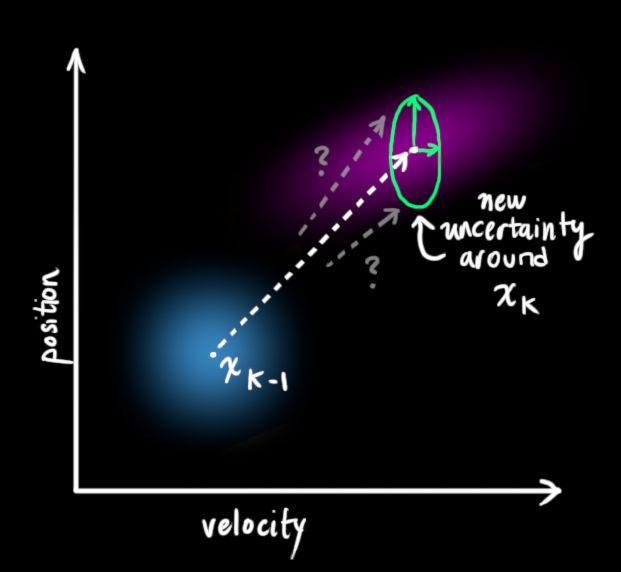
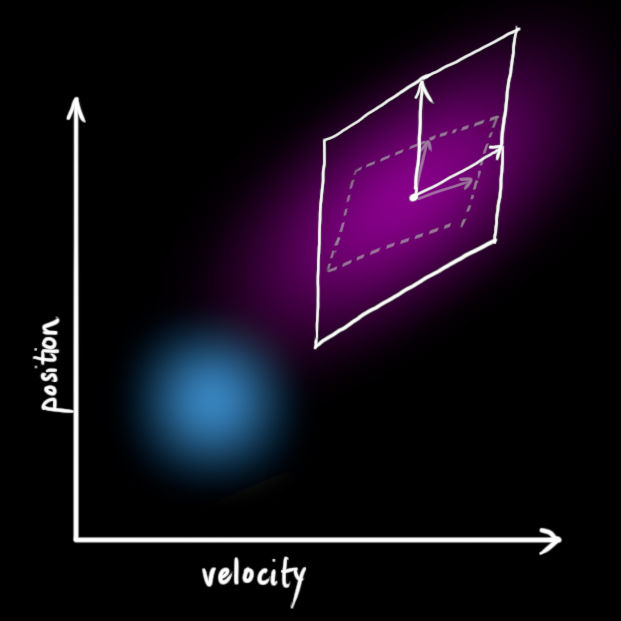
对 $Q_k$ 简单叠加，可以得到扩展的方差，这样就得到了完整的预测转换方程：
$$\begin{array}{l}{\hat{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k\overrightarrow{{\mathbf{u}}_k}\\ {\mathbf{P}}_k={\mathbf{F}}_{\mathbf{k}}{\mathbf{P}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\end{array}$$新的预测转换方程只是引入了已知的可以预测的外力影响因素。
新的不确定性可以通过老的不确定性计算得到，通过增加外界无法预测的、不确定的因素成分。
在这里，一个模糊的估计范围就得到了，一个通过 $x_k$ 和 $P_k$ 描述的范围。之后还要结合传感器的数据。

4.4 通过测量值精炼预测值

我们可能还有一些传感器来测量系统的状态。目前我们不用太关系所测量的状态变量是什么，也许一个测量位置一个测量速度。每个传感器可以提供一些关于系统状态的数据信息，每个传感器检测一个系统变量并且产生一些读数。

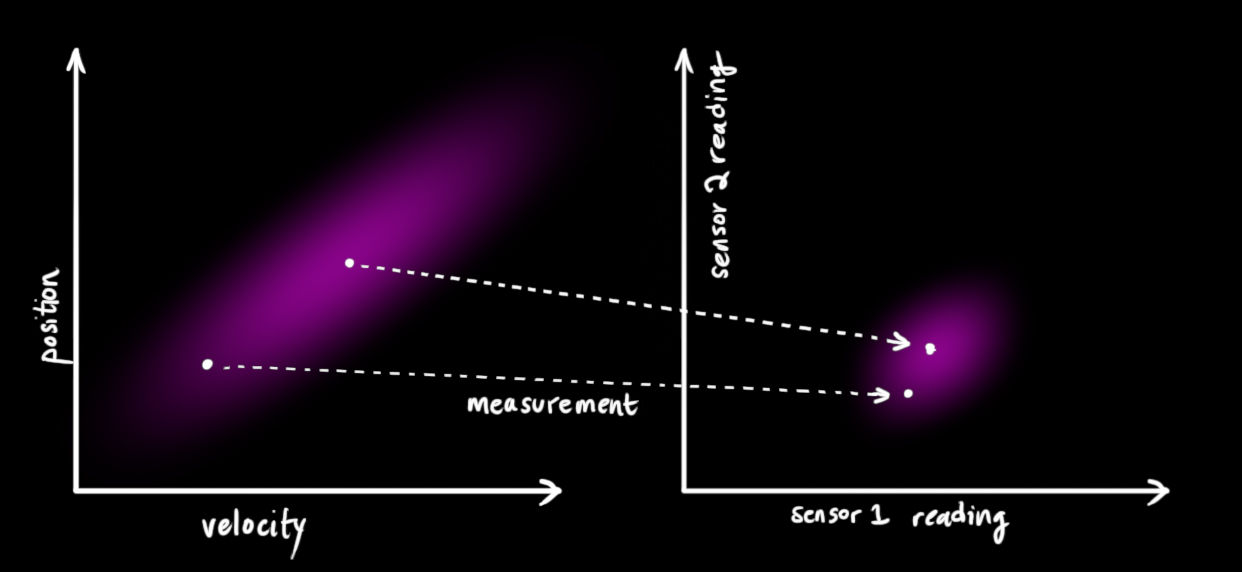
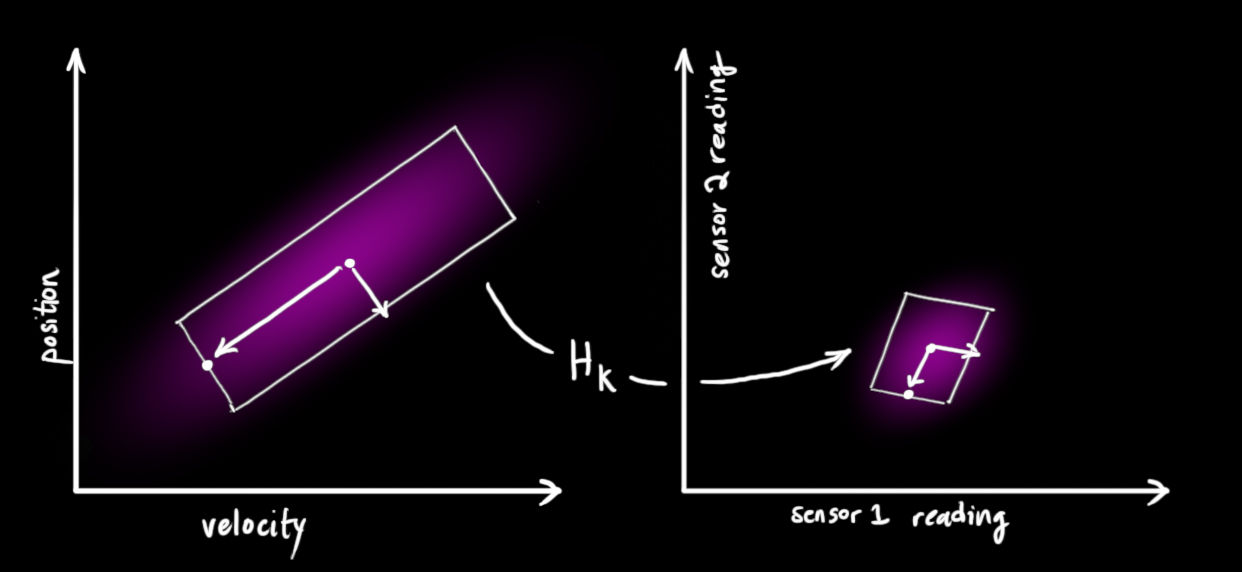
注意传感器测量的范围和单位可能与我们跟踪系统变量所使用的范围和单位不一致。我们需要将状态向量映射到传感器的测量空间中，通过矩阵 $H_k$ 我们可以得到传感器读数分布的范围：

$$\begin{array}{l}{\vec{\mu }}_{\text{expected }}={\mathbf{H}}_k{\hat{\mathbf{x}}}_k\\ {\mathbf{\Sigma }}_{\text{expected }}={\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T\end{array}$$

卡尔曼滤波也可以处理传感器噪声。换句话说，我们的传感器有自己的精度范围，对于一个真实的位置和速度，传感器的读数受到高斯噪声影响会使读数在某个范围内波动，左图中框出来的，为右图所示。我们观测到的每个数据，可以认为其对应某一个真实的状态。但是因为不确定性，某些状态的可能性比另外一些可能性更高：

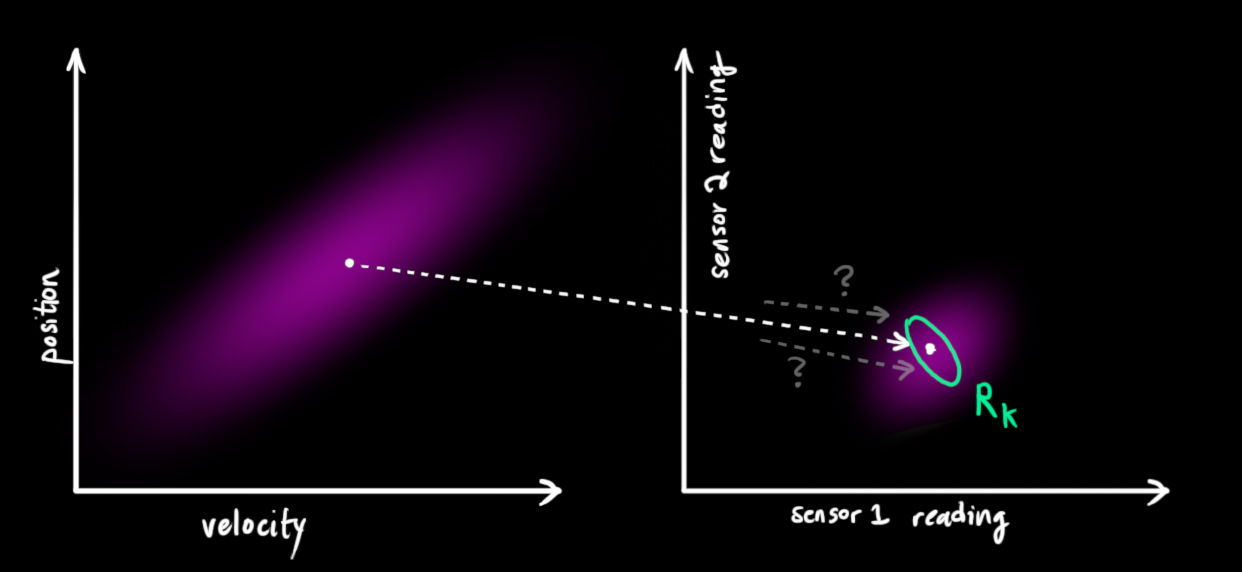
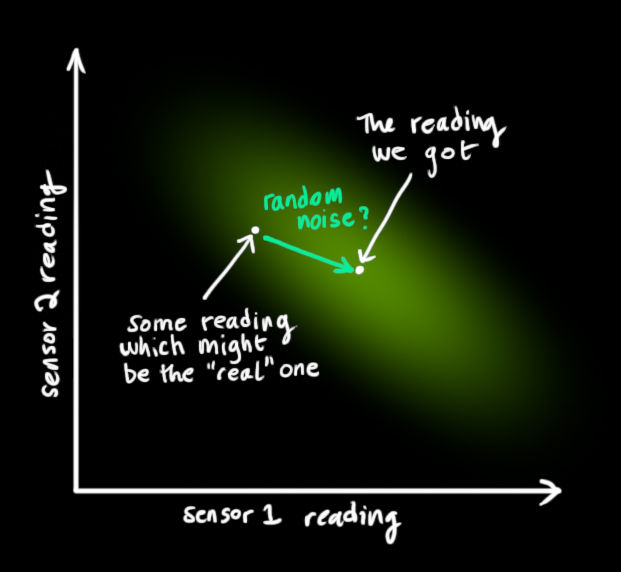
我们将这种不确定性的方差描述为 $R_k$，读数的平均值为 ${\bar{z}}_k$。
现在我们有了两个高斯斑，一个来自于我们的预测值 $Q_k$，另一个来自于我们的测量值 $R_k$，如下图所示：

我们必须尝试去把两者的数据预测值与观测值（绿色）融合起来。
所以我们得到的新的数据会长什么样子呢？对于任何状态$(z_1,z_2)$，我们有两个可能性：
（1）传感器读数更接近系统真实状态
（2）预测值更接近系统真实状态。

如果我们有两个相互独立的获取系统状态的方式，并且我们想知道两者都准确的概率值，我们只需要将两者想成，将两个高斯斑相乘，如下左：

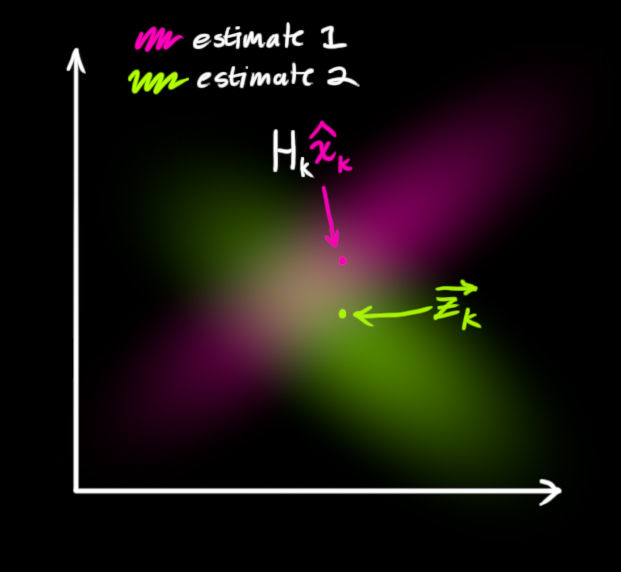
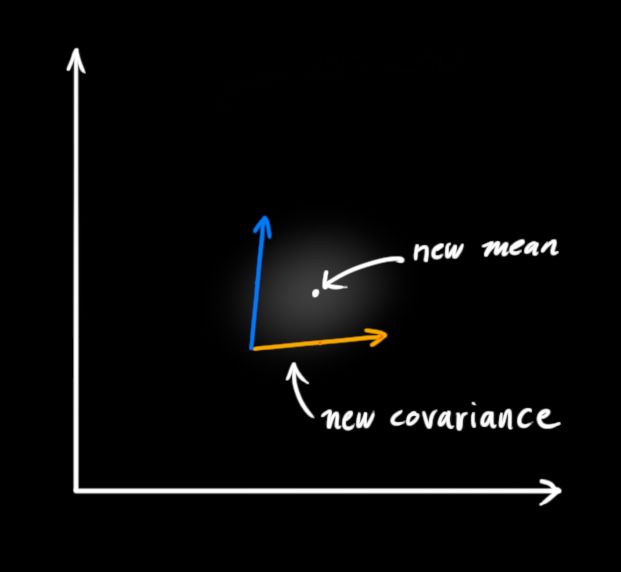
相乘之后得到的即为重叠部分，这个区域同时属于两个高斯斑。，且比单独任何一个区域都要精确。这个区域的平均值取决于我们更信赖哪个数据来源，这样我们也通过我们手中的数据得到了一个最好的估计值，如上右，看上去像另一个高斯斑。

4.5 修正

来到了卡尔曼滤波最关键的一步：融合预测和观测的结果，充分利用两者的不确定性来得到更加准确的估计。即，如何得到上右图中最好的那个估计。

已知预测结果服从高斯分布：
$$({\vec{\mu }}_{exp},{\Sigma }_{exp})=({\mathbf{H}}_k{\hat{\mathbf{x}}}_k,{\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T)$$

已知观测结果服从高斯分布：
$$({\vec{\mu }}_{meas},{\Sigma }_{meas})=(z_k,R_k)$$

4.5.1 两个高斯概率密度函数的乘积

下面给出两个高斯概率密度函数相乘的推导过程：
$$\begin{array}{l}f(x)=\frac{1}{\sqrt{2\pi }{\sigma }_f}{e}^{-\frac{{\left(x-{\mu }_f\right)}^2}{2{\sigma }_f^2}}\text{ and }g(x)=\frac{1}{\sqrt{2\pi }{\sigma }_g}{e}^{-\frac{{\left(x-{\mu }_g\right)}^2}{2{\sigma }_g^2}}\\ \begin{array}{rl}f(x)g(x)& =\frac{1}{2\pi {\sigma }_f{\sigma }_g}\exp \left[-\frac{{\left(x-{\mu }_{fg}\right)}^2}{2{\sigma }_{fg}^2}\right]\exp \left[-\frac{{\left({\mu }_f-{\mu }_g\right)}^2}{2\left({\sigma }_f^2+{\sigma }_g^2\right)}\right]\\ =& \frac{1}{\sqrt{2\pi }{\sigma }_{fg}}\exp \left[-\frac{{\left(x-{\mu }_{fg}\right)}^2}{2{\sigma }_{fg}^2}\right]\frac{1}{\sqrt{2\pi \left({\sigma }_f^2+{\sigma }_g^2\right)}}\exp \left[-\frac{{\left({\mu }_f-{\mu }_g\right)}^2}{2\left({\sigma }_f^2+{\sigma }_g^2\right)}\right]\end{array}\end{array}$$从上式可以看出，我们求解得到新高斯分布的均值和方差分别为:
$$\begin{array}{rl}{\mu }^{\prime }& =\frac{{\sigma }_0^2{\mu }_1+{\sigma }_1^2{\mu }_0}{{\sigma }_0^2+{\sigma }_1^2}={\mu }_0+\frac{{\sigma }_0^2\left({\mu }_1-{\mu }_0\right)}{{\sigma }_0^2+{\sigma }_1^2}\\ {\sigma }^{\prime 2}& =\frac{1}{\frac{1}{{\sigma }_0^2}+\frac{1}{{\sigma }_1^2}}={\sigma }_0^2-\frac{{\sigma }_0^4}{{\sigma }_0^2+{\sigma }_1^2}\end{array}$$

从图中可以看出，左右两个不确定的高斯分布更新后得到中间那个更确定的高斯分布($\sigma$小于左右两的$\sigma$值)。

4.5.2 新的卡尔曼增益

我们把关注点放在该乘积中新的高斯概率密度函数，它描述了一个新的高斯分布，这正是卡尔曼滤波想要的最优估计。在新的均值和方差计算公式中，我们令：
$$\mathbf{k}=\frac{{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}$$那么可以得到：
$$\begin{array}{rl}{\mu }^{\prime }& ={\mu }_0+k({\mu }_1-{\mu }_0)\\ {\sigma }^{\prime 2}& ={\sigma }_0^2-k{\sigma }_0^2\end{array}$$将它们写成矩阵形式就是：
$$\begin{array}{rl}\mathbf{K}& ={\Sigma }_0{\left({\Sigma }_0+{\Sigma }_1\right)}^{-1}\\ {\vec{\mu }}^{\prime }& =\overrightarrow{{\mu }_0}+\mathbf{K}\left(\overrightarrow{{\mu }_1}-\overrightarrow{{\mu }_0}\right)\\ {\Sigma }^{\prime }& ={\Sigma }_0-\mathbf{K}{\Sigma }_0\end{array}$$前面我们已经得到了预测结果和观测结果服从的两个高斯分布:
$$\begin{array}{rl}({\vec{\mu }}_{exp},{\Sigma }_{exp})& =({\mathbf{H}}_k{\hat{\mathbf{x}}}_k,{\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T)\\ ({\vec{\mu }}_{meas},{\Sigma }_{meas})& =(z_k,R_k)\end{array}$$所以我们可以进行如下推导，来得到卡尔曼滤波对当前状态(基于预测和观测的)最优估计的计算方程：
$$\begin{array}{rl}\mathbf{K}& ={\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T{\left({\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)}^{-1}\\ {\mathbf{H}}_k{\hat{\mathbf{x}}}_k^{\prime }& ={\mathbf{H}}_k{\hat{\mathbf{x}}}_k+\mathbf{K}\left(z_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_k\right)\\ {\mathbf{H}}_k{\mathbf{P}}_k^{\prime }{\mathbf{H}}_k^T& ={\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T-\mathbf{K}{\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T\end{array}$$两边化简下，注意 $\mathbf{K}$ 可以展开，就可以得到传说中的 卡尔曼增益：
$$\begin{array}{rl}\mathbf{K}& ={\mathbf{P}}_k{\mathbf{H}}_k^T{\left({\mathbf{H}}_k^T{\mathbf{P}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)}^{-1}\\ {\hat{\mathbf{x}}}_k^{\prime }& ={\hat{\mathbf{x}}}_k+\mathbf{K}\left(z_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_k\right)\\ {\mathbf{P}}_k^{\prime }& ={\mathbf{P}}_k-\mathbf{K}{\mathbf{H}}_k{\mathbf{P}}_k\end{array}$$

5.卡尔曼公式

预测未来
$\cdot$ 输入：过去的最优状态 $\left({\hat{\mathbf{x}}}_{k-1},{\mathbf{P}}_{k-1}\right)$，外界对过程的影响 ${\overrightarrow{\mathbf{u}}}_k$，环境的不确定度 $Q_k$。
$\cdot$ 输出：经过测量修正的最优状态 $\left({\hat{\mathbf{x}}}_k,{\mathbf{P}}_k\right)$。
$\cdot$ 其他：对过程的描述 $\left({\mathbf{F}}_{\mathbf{k}},{\mathbf{B}}_{\mathbf{k}}\right)$ 跟时间有关。
$$\begin{array}{rl}{\hat{\mathbf{x}}}_k& ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k\overrightarrow{{\mathbf{u}}_k}\\ {\mathbf{P}}_k& ={\mathbf{F}}_{\mathbf{k}}{\mathbf{P}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\end{array}$$修正当下
$\cdot$ 输入：预测的最优状态 $\left({\hat{\mathbf{x}}}_k,{\mathbf{P}}_k\right)$，测量的状态分布 $\left(\overrightarrow{{\mathrm{z}}_k},{\mathrm{R}}_k\right)$，预测到测量的变换矩阵 $H_k$。
$\cdot$ 输出：经过测量修正的最优状态 $\left({\hat{\mathbf{x}}}_k^{\prime },{\mathbf{P}}_k^{\prime }\right)$。
$$\begin{array}{c}{\hat{\mathbf{x}}}_k^{\prime }={\hat{\mathbf{x}}}_k+{\mathbf{K}}^{\prime }\left(\overrightarrow{{\mathbf{z}}_k}-{\mathbf{H}}_k{\hat{\mathbf{x}}}_k\right)\\ {\mathbf{P}}_k^{\prime }={\mathbf{P}}_k-{\mathbf{K}}^{\prime }{\mathbf{H}}_k{\mathbf{P}}_k\\ {\mathbf{K}}^{\prime }={\mathbf{P}}_k{\mathbf{H}}_k^T{\left({\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)}^{-1}\end{array}$$

6. 在 Radar 和 Ladar 上的应用

大致的滤波步骤如下图所示：

以车辆检测自行车为例，卡尔曼滤波算法被分为以下步骤：

• 1.第一次测量：滤波将会收到自行车相对于车辆位置的初始测量。测量值来自于激光雷达或者雷达传感器。
• 2.初始化状态和协方差矩阵：滤波将基于第一次测量初始化自行车的位置。
• 3.预测：算法将会预测在时间 $\Delta t$ 之后自行车的位置。一个比较基础的预测自行车在 $\Delta t$ 时间之后位置的方法是假设自行车速度是恒定的。
• 4.更新： 滤波器会将“预测”的位置与传感器测量结果进行比较。将预测的位置和测量的位置结合起来给出一个更新的位置。根据每个值的不确定性，卡尔曼滤波将在预测位置或测量位置上赋予更多的权重。
• 随后汽车将在一段时间 $\Delta t$ 后收到另一个传感器的测量结果。然后，该算法进行下一个预测和更新步骤

更新流程如下：

3. Kalman Filter 方程

现在用一个一维运动作为示例，目标是使用状态 $x$，即位置和速度来跟踪行人：
$$x=\left(\begin{array}{l}p\\ v\end{array}\right)$$

3.1 预测步骤

当设计卡尔曼滤波的时候，我们已经定义了两个线性方程：状态转换函数F和测量函数H。

• 状态转换函数 $F$ (state transition function)
  $x^{\prime }=Fx+Bu+\nu$ ---------其中 $Bu$ 即外力通常为0; $noise$ $\nu \sim N(0,Q)$
  其中，
  $F=\left(\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right)$
  $x^{\prime }$ 为在时间 $\Delta t$ 后预测的物体。
  
  在使用恒定速度的线性运动模型后，一个新的位置，$p^{\prime }$ 被计算为：
  $p^{\prime }=p+v\Delta t$ (为 $x^{\prime }=Fx$ 推导得)
  其中 $p$ 是老距离，速度 $v$ 与新速度相同因为速度是恒定的。
  我们可以使用以下矩阵形式表示：
  $\left(\begin{array}{l}{p}^{\prime }\\ v^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right)\left(\begin{array}{l}p\\ v\end{array}\right)$
  
  在表示物体位置和速度的时候，看做以 $x$ 为均值的高斯分布。
  在方程 $x^{\prime }=Fx+noise$ 内，我们用状态向量计算的为均值。
  噪声由均值为0的高斯分布表示；因此，$noise=0$ 代表均值噪声为0，此时函数为 $x^{\prime }=F\ast x$。
  
  然而噪声确实存在不确定性，用矩阵 $Q$ 表示。
  
  $P^{\prime }=FP{F}^T+Q$

3.2 更新步骤(纠正步骤)

在更新步骤中，我们使用测量函数将状态向量映射到传感器的测量空间中。举例来说，激光雷达只测量物体的位置。但扩展卡尔曼滤波模型的对象的位置和速度。所以乘以测量函数 $H$ 矩阵就会从状态向量 $x$ 中去掉速度信息。然后将激光雷达的测量位置与我们对目标位置的判断进行比较。
$z=H{x}^{\prime }+\omega$ 其中 $noise$ $\omega \sim N(0,R)$
其中 $\omega$ 代表传感器测量噪声。
所以对于雷达，测量函数是像这个样子的：
$z=p^{\prime }$
它也可以表示为一个矩阵形式：
$z=\left(\begin{array}{ll}1& 0\end{array}\right)\left(\begin{array}{l}{p}^{\prime }\\ v^{\prime }\end{array}\right)$

点击跳转：
滤波笔记二：无迹卡尔曼滤波 CTRV&&CTRA模型.
滤波笔记三：粒子滤波.
滤波笔记四：扩展卡尔曼滤波.