WBC理论及人形WBC代码详解

WBC理论及青龙WBC

1、 知乎，基于零空间的WBC

https://zhuanlan.zhihu.com/p/633715817

  雅克比矩阵是由机器人当前构型决定的，也就是关节角度确定的，当存在冗余自由度时，其不同的雅克比矩阵可执行同样的任务，或者理解为一个机械臂其高度方向的任务雅克比矩阵是可以去掉水平旋转关节的。

这里指满足任务后，也就是关节已经有角速度，依然存在这样的关节速度组合（存所有关节的速度被约束为一种关系，其中有关节可能需要满足速度不能再变），使得机器人几个关节速度有变化，但末端速度不变。

所以认为是使得末端速度为零的关节速度的组合，满足N这个关系后实现。这里阐述有冗余自由度的情况。

这里给了两个可以同时满足的任务，可以从位置任务和姿态任务的角度理解，好区分一些，但实际是可以叠加的。

这里X*是期望的末端速度，这里q0必须要经过N1这个关系才能到关节去，也就是可以随便给q0,都不会影响最终的x*。

 

这里任务2的关节速度实际上是在任务1的基础上，寻找合理的q0,也就是约束： = .

2 cSDN ，零空间基本原理

这里*代表期望，W是末端的速度，是任务W下的有冗余自由度的对应的雅克比矩阵的伪逆。

这里与知乎原文基本一致。

给定了关节角和构型。

期望末端速度为1 ， 1.平面的

那么关节速度就是雅克比伪逆的关系

这里直接使用雅克比计算，从而得到计算的和期望末端速度的一致

期望第一 第二关节的速度为0，并满足末端{1,1}的速度， 直观上讲，这是不可能的，但如果两个任务都给同样的权重。 应该如何计算？

如何理解这里的雅克比矩阵？

这里给的雅克比任务矩阵右乘关节角 = 笛卡尔速度（两个平面速度，并且分别只受前两个关节影响），在给定任务时，一般是末端的任务，所以这里可以理解为其进行了一个巧妙的转换，给定了一个末端的任务雅克比矩阵，直接表征一二关节。

形成了一个方程组。一并计算结果，雅克比伪逆左乘末端期望

这时候解算出一个关节结果。显然，如果使用这个关节结果，两个任务的期望都不能满足。

但可以得到期望的平方差。

如果只满足任务一，不管关节速度的任务，那么任务平方差如上。

在这个有冗余自由度的例子中，如果满足任务一，那一定是可以更好的逼近任务二的，使用零空间理论求解任务一下的任务二的更好的情况。

按前面的知乎文章的详细推导，可知，先求零空间的投影，再通过两个任务要求反求满足任务一后的q0,然后求关节角速度。这里使用了逆矩阵求解最优。

3、知乎机械狗，https://zhuanlan.zhihu.com/p/641297823

  

阐述了机械狗在动态运动过程的欠约束情况下的，WBC的作用。

这些任务都作用在关节上，为了同时满足更多的任务要求，任务有冲突时，偏向于高优先级。

4 论文 北航四足MPC+WBC 

阐述了速度多任务的零空间控制，q0也满足该公式，其中，q-1的零空间是所有的，也就是N-1为单位矩阵。

这里解释了如何利用WBC跟踪末端位置任务，delta_q 是关节的位置期望与实际差，e是笛卡尔的期望与实际位置差。若没有其他任务，关节期望位置（q_des）直接就是关节当前位置(q_cur) + 关节位置差（delta_q）(运动学逆解直接算)。但有了多任务，delta_q就要重新算一下，按优先级来，本文公式是零空间的。实际上是利用位置差借用了速度任务的公式

机器人学导论中标准的关节加速度与笛卡尔加速度的关系，这里使用了雅克比的时间导数。dJ,

5 基于二次规划的WBC（知乎）

二次规划问题：最小化一个二次项和线性项的二范数。优势在于求解不等式的约束

允许不那么严格的执行任务，也就是在寻找最优时，离最优正负s1区间内的值都是最优的可选的。即便无解，也要找出偏近的解。

6 北航四足论文  全身控制的使用

这里非常清晰的给出浮动基的定义及使用，以及为什么一般广义坐标的定义为Body在世界的位置、姿态 加上其余关节 （q_body + q_joint）

注：欧拉角的一个角是基于另外两个角度变化的，是一个相对角度，所以这里用了四元数表示。

注意：一般定义的广义速度和广义加速度的其中的body的量：是基于body坐标系下的角度，角加速度，基于body坐标系下的线速度和线加速度。

注意：浮动基机器人的动力学是直接按广义坐标可计算的，这里将重力项包进了C矩阵，是基于关节而非笛卡尔的状态空间方程，广义关节位置、速度、加速度产生广义关节力矩，这里因为广义位置前六个是基于世界坐标系的，或者速度加速度也会产生非零的力矩，而虚拟6自由度关节无法产生基于它的基坐标系的力矩，过滤掉，这就是欠约束机器人，当机器人单脚或悬空时，变为高度欠约束。

而这里为什么会有接触力*雅克比 ？从静力学公式将，外力通过雅克比转置映射到关节，也就是关节本身所承载的外力需要计算进去。

这也就要求的机器人的外力能够对关节产生力矩，需要小的减速比，小的摩擦。

总的来说，公式(4.34)右边是系统受到的力，包含外部环境提供的接触力和系统内部

的关节力；左边是系统当前状态以及在这些力的作用下实现的运动。

支撑腿需要让质心产生移动，从而这里作为最重要的任务，这里的转动任务就是转弯的遥控，平动的任务就是前后左右的遥控，需要跟上遥控的指令？这里也是支撑腿的跟踪轨迹？

求得动力学参数后。那么左边是广义关节位置、速度、加速度。右边是关节合力矩（浮动基前6个转成0）.那么这里为什么可以求到期望的位置、速度和加速度？

伪代码第二行：期望的关节加速度，其实这里是笛卡尔加速度到关节加速度的标准的转换，只不过笛卡尔期望加速度为0.

对于支撑腿：

获得笛卡尔位置差-》获得笛卡尔的期望的加速度（用参数来调节）-》求零空间矩阵-》求期望位置（通过求位置的变化差，套用速度雅克比求得的）-》求得期望速度和期望的加速度

因此，这里只是通过期望的迪卡尔的位置和速度以及（自己调节的PD参数的加速度）的任务，得到最终的基于多任务的基于零空间的关节位置、速度、加速度的优化计算后的期望值

1 将Body的角度转到世界坐标系的四元数表示计算或者使用这里的近似线性化。从而得到body的yaw的误差。

解答了任务问题，将任务1 看成了支撑腿的运动学逆解，对于该任务，那么期望笛卡尔的速度，加速度也就是0.

任务2 相对世界的期望角速度是遥控器给的。给的是Body相对于对于世界的角速度。雅克比的行数是笛卡尔空间下的自由度，列数是操作臂自由度，这里将body浮动基位置的任务及驱动关节的雅克比全改成0；

同上，任务3的雅克比矩阵给出了body相对于世界坐标系的位置，姿态，及全部为0的关节。

这里明确解释了外力作用到关节时，对机器人动力学的影响，及如何利用动力学求解相应的关系。

MPC通过单刚体动力学推导预测出最佳的足端反力，WBC得到了广义加速度，要抵消足端的作用力保持body稳定，就会得到一个关节加速度，但WBC依据任务也有个关节加速度，所以二者需要妥协一下，各自让步。

那么二者之间简单的就是权重问题，但为了保证约束与最优，。。。略

总之就是解出了松弛量，从而带入已经求出的关节加速度和足反力（影响的关节加速度），通过考虑外力作用的关节空间的动力学方程，计算得出应该施加的关节力矩。

这里关节位置就是当前关节位置，这里的关节速度是当前读取的关节速度，当前的构型也就是关节角决定了雅克比矩阵，所以这里雅克比矩阵，M矩阵，C矩阵都是需要实时算的。

最终发给电机的是这个。

综上：利用WBC零空间，按不同任务的优先级，给定期望任务然后计算，得到了期望的关节位置、速度、加速度。并对刚刚的关节加速度、足端反力行优化，最终通过动力学（）计算得出关节的前馈力矩，然后加上关节PD控制（WBC得出的期望位置和速度，电机实际反馈的位置和速度）发给电机

7 基于优化的WBC（二次规划计算关节力矩）：

1 二次规划问题：

2：二次规划总结：

3 一个例子表明优化状态和约束状态关系

8 青龙WBC代码解读

//参考：说明文档

//  https://zhuanlan.zhihu.com/p/704483759

//  https://atomgit.com/openloong/openloong-dyn-control

//  WBC — OpenLoong Dynamics Control documentation

注：本文对WBC求解前馈力矩时的具体解释并不清晰

1WBC在哪里起作用

从代码中可以看到，它拿到期望的一些信息，主要是遥控器给定的速度，期望的高度及步态调度后的一些位置姿态。

然后算一下关节期望的位置、速度、力矩。

然后给到关节PVT控制了。

2 WBC的输入，dataBusRead()函数

3 WBC的输出dataBusWrite()函数

4 第一部分，WBC根据给定任务计算期望位置、速度、加速度，

已经明确了输入输出，接下来看计算

这里计算其实还是依据零空间理论，进行位置、速度、加速度任务，和狗一样

1先看看定义了哪些任务

主要是一些关于Body姿态的任务，比较丰富，一般是姿态优先，速度跟踪其次，摆动腿最后。

2 具体看看一个任务怎么给定的：

和其他任务类似，并不是给了一个笛卡尔具体的速度任务，而是比较有一个明确的期望状态作为任务，计算了状态的速度和速度差，并且为了计算关节加速度，给了位置系数和速度系数，核心是给定了任务雅克比矩阵。

ID其实就是任务优先级，addTask在前面的优先级高。

3 给完了任务，接下来看看按照任务，最终能得出什么

4 详细计算过程：computeAll()

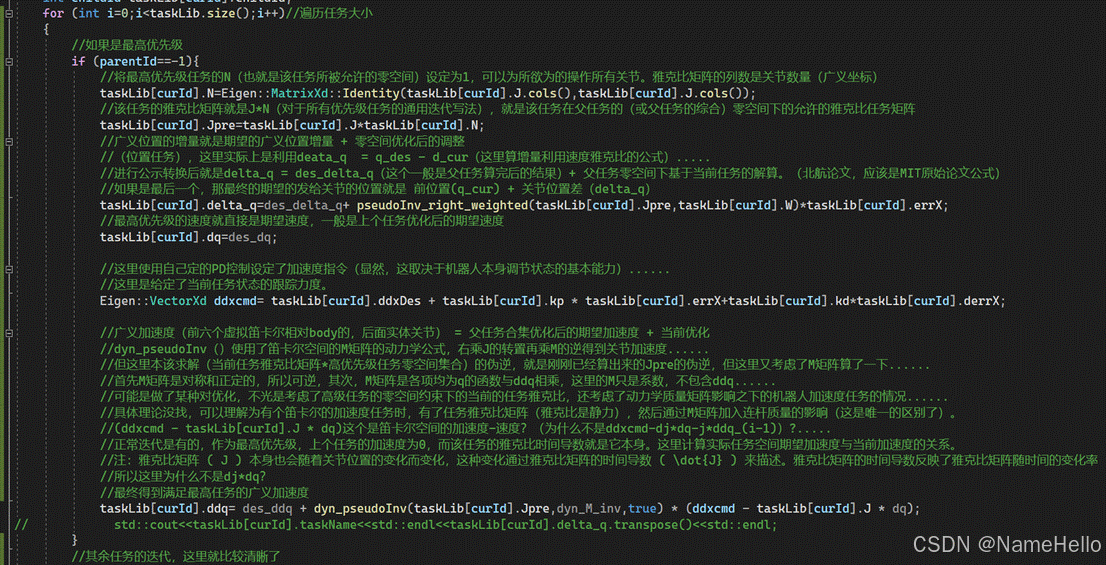
按狗来的，没变，与北航论文中基本一致

已经知道了，算出如下内容

5第二部分，WBC根据广义加速度和地面反力计算关节前馈力矩，void WBC_priority::computeTau()

地面反力一般是MPC计算的，属于控制的范畴，就是让支撑腿实现质心轨迹的跟踪。

以下代码是computeTau()的连续的代码

这里建立了QP问题，旨在按权重寻找出既让期望浮动基的六维加速度与期望的12维度外力，在满足约束的情况下，输出误差最小的值。

显然，二者是存在关系并且有冲突的，不然就剩下满足约束了。内有动力学的关系约束

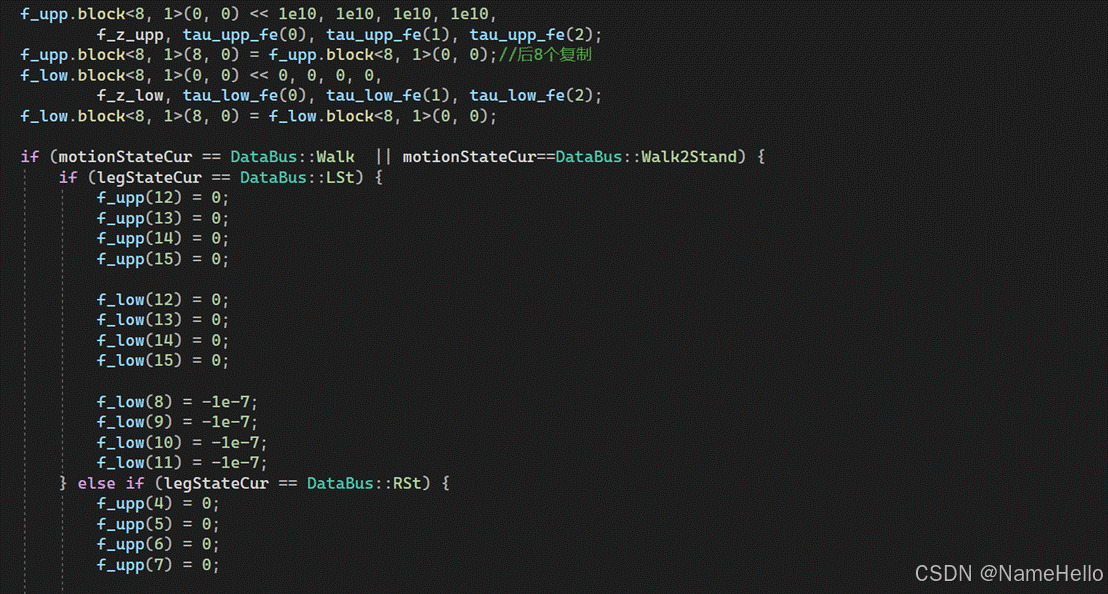
至此，在MPC计算的反力跟踪质心轨迹、在WBC各状态任务下。计算了关节所需要的期望位置、速度、前馈力矩。