Lyapunov意义下的稳定性定义

如图所示的三个曲面，小球均处于平衡点，考虑其受扰动作用，自平衡点偏离后的系统响应。

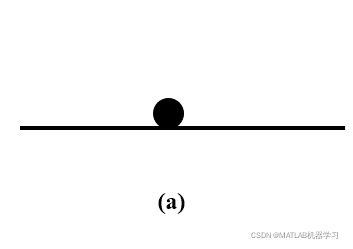
平衡点a:受扰动作用使得小球偏离原平衡点，并且使得小球达到另一个平衡点，小球的状态是自由响应且有界。

平衡点b:考虑有摩擦，小球绕原点平衡点将产生衰减振荡，小球的状态是自由响应且有界的，并且将最终返回自由平衡点。

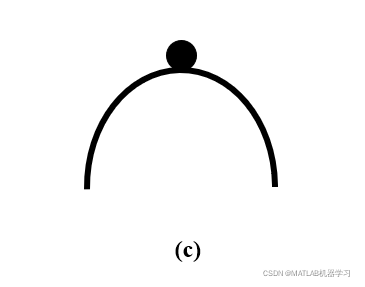
平衡点c:倘若受扰动作用使得小球偏离原平衡点，那么小球不一定能够达到下一个平衡点，那么就称小求的状态是自由响应且无界的。

1.稳定

1.1定义

设系统的初始状态$x_0$处在状态空间中，位于以平衡状态$x_e$为球心，半径为$\delta$的闭球域(Spherical Domain)$S(\delta )$内,即
$$\Vert x_0-x_e\Vert \le \delta ,t\ge t_0$$
若系统由初始状态$x_0$出发的系统自由响应$x(t;$$x_0$$,$$t_0$$)$在$t\to \infty$的过程中以平衡状态$x_e$