《考虑车辆运动约束的最优避障轨迹规划算法》论文解读二

无意2121

已于 2023-12-25 16:57:06 修改

阅读量1.6k

点赞数 2

分类专栏：自动驾驶决策规划与控制论文解读文章标签：算法自动驾驶几何学

于 2022-06-02 19:12:21 首次发布

本文链接：https://blog.csdn.net/weixin_65089713/article/details/125101947

版权

自动驾驶决策规划与控制论文解读专栏收录该内容

5 篇文章 14 订阅

订阅专栏

欢迎大家关注我的B站：

偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)

1 贝塞尔曲线

这篇论文通过贝塞尔曲线规划器生成局部轨迹，我们先介绍贝塞尔曲线的一些性质。

参考从零开始学图形学：10分钟看懂贝塞尔曲线 - 知乎 (zhihu.com)

贝塞尔曲线（Bezier Curve）原理、公式推导及matlab代码实现_beijing_txr的博客-CSDN博客_贝塞尔曲线

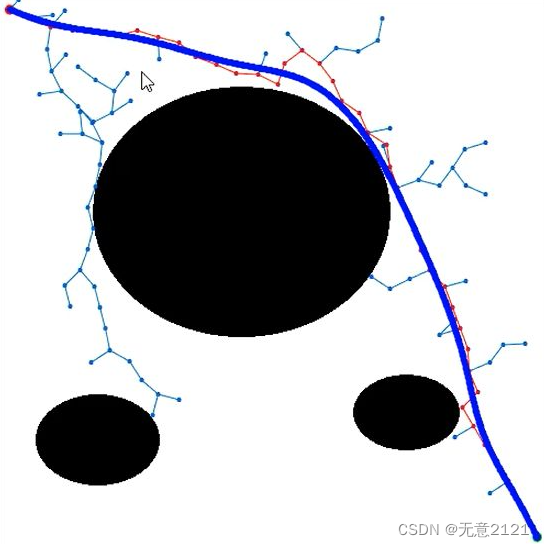
贝塞尔曲线是一种完全由控制点去控制曲线走向的曲线，如下图是利用贝塞尔曲线对rrt算法生成的散点为控制点，来生成平滑路径

1.1 公式推导

下面的P0和P1等等指的是向量或者向量的终点

$P(t)=P_{0}+(P_{1}-P_{0})*t=(1-t)P_{0}+tP_{1},t\in [0,1]$

一阶贝塞尔曲线公式如上，这是产生一个从P0运动到P1的点，而这个点所构成的轨迹就是贝塞尔曲线。那么二阶贝塞尔曲线也是类似，先产生一个由P0运动到P1的点，再产生一个由P1运动到P2的点，而产生的这两个点再产生一个由其中一个点运动到另一个点的点，最后这个点的轨迹就是二阶贝塞尔曲线。这里运动的过程是同步进行的。

$P(t)=(P_{0}+(P_{1}-P_{0})*t)+(P_{1}+(P_{2}-P_{1})*t)*t,t\in [0,1]$

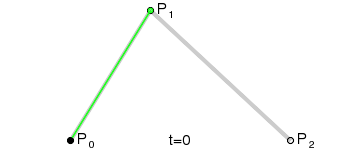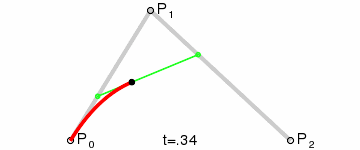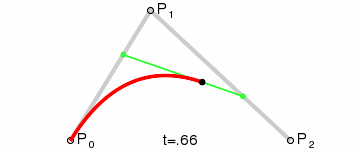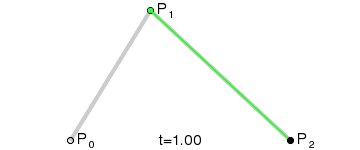
在这里插入图片描述

同理可得任意阶数的贝塞尔曲线都可以这样计算得到

阶数	示意图
三阶
四阶
五阶

很显然这是一个递归的过程，我们可以推出n阶贝塞尔曲线的函数是

$P(t)=\sum_{i=0}^{n}P_{i}B_{i,n}(t),t\in [0,1]$

$B_{i,n}=C_{n}^{i}t^{i}(1-t)^{n-i}=\frac{n!}{i!(n-i)!}t^{i}(1-t)^{n-i},t\in [0,1]$

从线性空间的角度来看，n+1个 $B_{i,n}$ 函数是线性无关的，恰好构成线性空间的n+1组基底，每个 $B_{i,n}$ 函数都称为Bernstein基函数

1.2 Bernstein基函数的性质

权性：每个向量之前的系数之和为1

$\sum_{i=0}^{n} B_{i,n}=1$

对称性：

$B_{i,n}(t)=B_{n-i,n}(1-t)$

导数：

$B{}'_{i,n}(t)=n(B_{i-1,n-1}-B_{i,n-1})$

最大值：

$B_{i,n}(t)$ 在 $t=\frac{i}{n}$ 时取得最大值

递推性：

$B_{i,n}(t)=(1-t)B_{i,n-1}(t)+tB_{i-1,n-1}(t)$

1.3 贝塞尔曲线的性质

$P{}'(t)=n\sum_{i=1}^{n}P_{i}n(B_{i-1,n-1}-B_{i,n-1})=n\sum_{i=1}^{n}(P_{i}-P_{i-1})B_{i-1,n-1}$

可见贝塞尔曲线的导数还是贝塞尔曲线.

$P{}'(0)=n(P_{1}-P_{0}),P{}'(1)=n(P_{n}-P_{n-1})$

由此可得 t=0 时贝塞尔曲线的起点的切线方向就是第一个点和第二个点的连线，终点的切线方向就是最后一个点和倒数第二个点的连线方向。上面是贝塞尔曲线切矢量的性质，同理可得贝塞尔曲线二阶导矢量的公式。

$P{}''(t)=n(n-1)\sum_{i=1}^{n-1}(P_{i+1}-2P_{i}+P_{i-1})B_{i-1,n-2}(t)$

$P^{(k)}(t)=n(n-1)\cdots (n-k+1)\sum_{i=1}^{n-k}P_{i-1}^{(k)}B_{i-1,n-k}(t)$

具体的公式推导可以参考贝塞尔曲线的求导、弧长参数化与分段拟合方法 - 知乎 (zhihu.com)

1.4 曲线的连续性

当我们讨论两条曲线的拼接时，需要考虑其连续性

（1）位置连续：也就是一条曲线的末端与另一条的始端重合，称为C0连续

（2）斜率连续：在位置连续的基础上，一条曲线末端切向量与另一条始端切向量方向相同模长相等，则称为C1连续，若仅是方向相同，则成为G1连续

（3）曲率连续：在位置连续和斜率连续的基础上，一条曲线末端二阶导向量与另一条始端二阶导向量方向相同模长相等，并且主法线方向一致，称为C2连续，若仅是二阶导向量在另一二阶导向量与切向量构成的平面内，称为G2连续

曲率公式：

$\kappa =\frac{\left |P{_{i}}'(t)\times P{}''_{i}(t)\right |}{\left | P{_{i}}'(t)\right |^{3}}$

2 贝塞尔曲线规划器

2.1 局部轨迹

前面对贝塞尔曲线进行了比较详细的介绍，我们发现贝塞尔曲线可以通过几个控制点迅速局部修改曲线的形状，这为我们固定始末两点，生成多条局部轨迹提供了便利。

贝塞尔曲线的计算成本随着阶数的升高而升高，我们选择可生成连续曲率的最小阶数曲线，也就是三阶贝塞尔曲线进行局部轨迹的生成，一些基本公式如下

我们现在需要将局部生成的轨迹和原来行驶的轨迹进行衔接。要让局部轨迹在起点和终点与直线路段（已经经过frenet转换）是满足C2连续的。

因此P0与P1在同一水平线上，P2与P3在同一水平线上，但这时候仍旧不能满足C2连续，只能通过增加P0与P1之间的距离或者增加P2与P3之间的距离来使曲率在始末位置趋于0。下图是通过调整P0与P1之间的距离，改变局部轨迹。

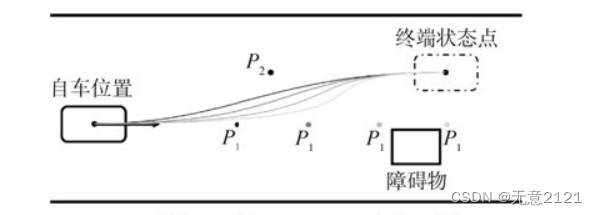
2.2 约束

（1）曲率连续约束：曲率在始末位置要能连续过渡到原始轨迹上

（2）车辆运动学约束：车辆存在最小转弯半径，因此轨迹任一点曲率半径大于等于最小转弯半径

（3）车辆动力学约束：防止车辆发生侧滑或侧倾，对侧向加速度，横摆角速度以及侧向急动度进行约束

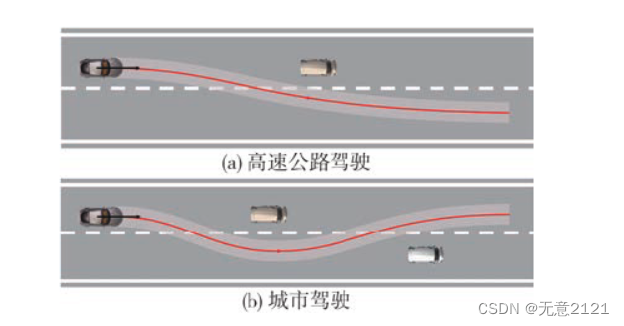
不满足三种约束的需要重新修正贝塞尔曲线的控制点位置。仿真结果如下

无意2121

关注

2
点赞
踩
15

收藏

觉得还不错? 一键收藏
打赏
1
评论
《考虑车辆运动约束的最优避障轨迹规划算法》论文解读二

一阶贝塞尔曲线公式如上，这是产生一个从P0运动到P1的点，而这个点所构成的轨迹就是贝塞尔曲线。那么二阶贝塞尔曲线也是类似，先产生一个由P0运动到P1的点，再产生一个由P1运动到P2的点，而产生的这两个点再产生一个由其中一个点运动到另一个点的点，最后这个点的轨迹就是二阶贝塞尔曲线。（3）曲率连续：在位置连续和斜率连续的基础上，一条曲线末端二阶导向量与另一条始端二阶导向量方向相同模长相等，并且主法线方向一致，称为C2连续，若仅是二阶导向量在另一二阶导向量与切向量构成的平面内，称为G2连续。...
复制链接

扫一扫