Line Intersection using Bentley Ottmann Algorithm Tutorials & Notes | Math | HackerEarth
目录
一、说明
在计算几何中，Bentley-Ottmann 算法是一种扫描线算法，用于列出一组线段中的所有交叉点，即它找到线段的交点（或简称为交点）。它扩展了 Shamos–Hoey 算法。用于测试一组线段是否有任何交叉点。对于包含的输入n 个线段与，k 个交叉点（或交叉路口），Bentley–Ottmann 算法需要时间 O( (N+k)logN )
二、问题描述
给定一组 N 条线段（2*N 点），你需要找到这些线段之间的所有交点。
也许，您首先想到的是一种天真的方法来检查所有线段对是否相交。但是你知道这不是一个好方法，因为如果我们的交叉点较少，它会包含不必要的计算。其次，它会以未排序的顺序给出交叉点。所以，我们需要一些替代方法来解决这个问题。
2.1 直线段限定在水平和垂直
我们可以使用线扫描技术解决这个问题。但是在解决这个问题之前，首先让我们只考虑水平和垂直线段。
问题：给定N条水平线段和垂直线段，我们需要找到水平线段和垂直线段的所有交点。在这里，我们不会考虑重合的端点相交。
方法：继续我们的事件和活动集的概念，让我们首先为这个问题定义它们。在这里，我们将考虑三种类型的事件：水平线段的开始、水平线段的结束和垂直线段。我们的活动集包含所有被扫描线切割的水平线段（按 y 坐标排序）。
虚线是扫描线，黑线是给定的水平线和垂直线，红线是任意时刻与扫描线相交的水平线。
我们的算法如下：
1. 当我们击中水平线段的起点时，我们将线（在我们的实现中，我们将插入起点）插入到我们的集合中。
2. 当我们击中水平线段的终点时，我们从集合中移除线段（实现中线段的起点）。
3. 当我们碰到一条垂直线时，我们检查集合中位于垂直线段起始和结束 y 坐标之间的所有线段，即，如果垂直线段由 (x1,y1) 和 (x1) 表示,y2), 我们检查位于 (y1,y2) 范围内的水平线段。
这就完成了我们的算法。那么，让我们跳到实现部分：
#define x second
#define y first
typedef pair<int,int >point;
struct event
{
point p1,p2;
int type;
event() {};
event(point p1,point p2, int type) : p1(p1), p2(p2),type(type) {}; //initialization of event
};
int n,e;
event events[MAX];
bool compare(event a, event b)
{
return a.p1.x<b.p1.x;
}
set<point >s;
void hv_intersection()
{
for (int i=0;i<e;++i)
{
event c = events[i];
if (c.type==0) s.insert(c.p1);//insert starting point of line segment into set
else if (c.type==1) s.erase(c.p2);//remove starting point of line segment from set, equivalent to removing line segment
else
{
for (typeof(s.begin()) it=s.lower_bound(make_pair(c.p1.y,-1));it!=s.end() && it->y<=c.p2.y; it++) // Range search
printf("%d, %d\n", events[i].p1.x, it->y);//intersections
}
}
}
int main ()
{
scanf("%d", &n);
int p1x,p1y,p2x,p2y;
for (int i=0;i<n;++i)
{
scanf("%d %d %d %d", &p1x, &p1y,&p2x, &p2y);
if(p1x==p2x) //if vertical line, one event with type=2
{
events[e++]=event(make_pair(p1y,p1x),make_pair(p2y,p2x),2);
}
else //if horizontal line, two events one for starting point and one for ending point
{
//store both starting points and ending points
events[e++]=event(make_pair(p1y,p1x),make_pair(p2y,p2x),0);
//store both ending and starting points, note the order in the second, this is because we sort on p1, so ending points first, then we remove a line when we hit its ending point , so we need its starting point for removal of line
events[e++]=event(make_pair(p2y,p2x),make_pair(p1y,p1x),1);
}
}
sort(events, events+e,compare);//on x coordinate
hv_intersection();
return 0;
} 复杂度分析：所有对事件的操作（insert,erase, lower_bound）都需要O(log(N))
时间，内循环运行 k 次，其中 k 是交叉点的数量。因此，上述算法的复杂度为O(Nlog(N)+k)
所以，下一个想到的问题是如果 k 是O(N*2)，所以在那种情况下我们的算法运行缓慢。这是对的，但想想如果我们有路口，然后我们得到相当大的加速。其次，如果我们只需要交叉点的数量而不是交叉点本身会怎么样。然后我们可以找到交叉点的数量使用二叉树结构的时间（通过将子树的大小存储在子树的根中）。
2.2 将问题复杂化线条不垂直的交点
让我们回到我们的问题，线条不一定是垂直或水平的。在那种情况下该怎么办？
A： 首先，让我们列出算法中的假设：
1.没有垂直线段。
2. 没有两条线段在它们的端点处相交。
3. 没有三个（或更多）路段有共同的交叉点。
4.线段的所有端点和所有交点具有不同的x坐标。
5. 没有两个段重叠。
B ：主要相交性判别原理：
1. 两条线相交，它们必须彼此相邻。因此，我们将只检查相邻线是否相交。
2. 当两条线段相交时，它们改变位置，即相交前在下方的线在上方，另一条线在下方。
C: 在开始算法之前，首先让我们定义事件和活动集。
扫描线算法的Events
事件：线段的端点、交点。（我们会在找到它们时插入交点）。在这里，我们将使用优先级队列作为我们的数据结构，因为由于交叉点的动态插入和删除，预排序将不起作用。让我们用 PQ 表示优先级队列
扫描线算法的Active Set
在任何时候，活动集都包含被扫描线切割的线段，按 y 坐标排序。让我们用 SL 表示这个活动集。伪代码：
Initialize PQ = all segment endpoints;
Initialize SL to be empty;
Initialize output intersection list IL to be empty;
While (PQ is nonempty) {
Let E = the next event from PQ;
If (E is a left endpoint) {
Let segE = segment of E;
Add segE to SL;
Let segA = the segment Above segE in SL;
Let segB = the segment Below segE in SL;
If (I = Intersect( segB with segA) exists)
Delete I from PQ;
If (I = Intersect( segE with segA) exists)
Insert I into PQ;
If (I = Intersect( segE with segB) exists)
Insert I into PQ;
}
Else If (E is a right endpoint) {
Let segE = segment of E;
Let segA = the segment Above segE in SL;
Let segB = the segment Below segE in SL;
Delete segE from SL;
If (I = Intersect( segA with segB) exists)
Insert I into PQ;
}
Else { // E is an intersection event
Add intersect point of E to the output list IL;
Let segE1 above segE2 be intersecting segments of E in SL;
Swap their positions so that segE2 is now above segE1;
Let segA = the segment above segE2 in SL;
Let segB = the segment below segE1 in SL;
If (I = Intersect( segE1 with segA) exists)
Delete I from PQ;
If (I = Intersect( segE2 with segB) exists)
Delete I from PQ;
If (I = Intersect(segE2 with segA) exists)
Insert I into PQ;
If (I = Intersect(segE1 with segB) exists)
Insert I into PQ;
}
remove E from PQ;
}
return IL;
}那是 Bentley Ottmann 算法，用于在给定 N 条线段时找到所有交叉点。让我们看一下图像以更好地理解它。
算法详解：
1）输入线段：（ P（x，y），P1（x，y））循环输入全部线段用PP1表示。
2）对所有的线段端点（包括P和P1）按照x坐标排序，上图排序结果是：
PQ = 【 A，B，C，D，B1，D1，A1，C1】
3）我们提取 PQ 中的最小值并将其作为我们的事件。所以，我们知道这个事件可能是左端点、右端点或交点。如图：扫描线对PQ扫描，扫到A
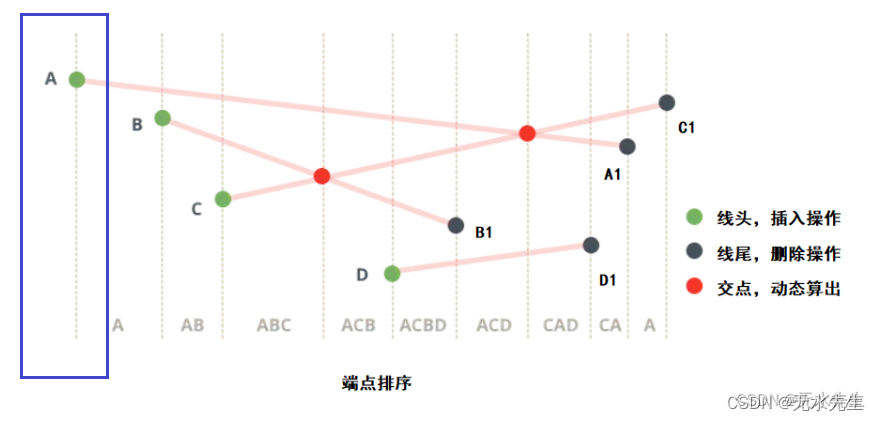A进入队列，（A是第一个点）
List = 【A】 表示唯一线段是A为起始点。
- 1 扫描线继续扫描PQ，找到B，比较A与扫描线交点W和B的y坐标，y(Wa)>y(B),表明A线段在B点上方，所以：
List = 【A，B】
- 2 继续扫描PQ序列，读出C点，因为y(C)<y(Wb)<y(Wa)，因此，C线段在最下方，
List = 【A，B，C】
- 3 继续扫描PQ序列，读出D点，此时，扫描线对应的交点按照y排序是是Wa，Wc，Wb，D
所以： List = 【A，C，B，D】
可以观察到，线序从【A，B，C】跳转到 List = 【A，C，B，D】 其中B和C产生一个逆序，因此，B和C有一个交点。（求出该交点保存）
- 4 继续扫描，看到B1点，因为B1点是个后端点，所以删除与之相对应的线段B：于是
List = 【A，C， D】
- 5 继续扫描，看到D1点，因为D1点是个后端点，所以删除与之相对应的线段D：计算扫描交点顺序： y(Wc) >y(Wa)
List = 【C，A】这里产生一个逆序，所以A和C两个线段必然相交，求出交点并保存。
- 6 继续扫描，看到A1点，因为A1点是个后端点，所以删除与之相对应的线段：计算扫描交点顺序： Wc > Wa
List = 【C 】 。
- 7 继续扫描，看到C1点，因为C1点是个后端点，所以删除与之相对应的线段：List = 【 】 。
算法结束。
三、相关实验代码
# lsi.py
# Implementation of the Bentley-Ottmann algorithm, described in deBerg et al, ch. 2.
# See README for more information.
# Author: Sam Lichtenberg
# Email: splichte@princeton.edu
# Date: 09/02/2013
from Q import Q
from T import T
from helper import *
# "close enough" for floating point
ev = 0.00000001
# how much lower to get the x of a segment, to determine which of a set of segments is the farthest right/left
lower_check = 100
# gets the point on a segment at a lower y value.
def getNextPoint(p, seg, y_lower):
p1 = seg[0]
p2 = seg[1]
if (p1[0]-p2[0])==0:
return (p[0]+10, p[1])
slope = float(p1[1]-p2[1])/(p1[0]-p2[0])
if slope==0:
return (p1[0], p[1]-y_lower)
y = p[1]-y_lower
x = p1[0]-(p1[1]-y)/slope
return (x, y)
"""
for each event point:
U_p = segments that have p as an upper endpoint
C_p = segments that contain p
L_p = segments that have p as a lower endpoint
"""
def handle_event_point(p, segs, q, t, intersections):
rightmost = (float("-inf"), 0)
rightmost_seg = None
leftmost = (float("inf"), 0)
leftmost_seg = None
U_p = segs
(C_p, L_p) = t.contain_p(p)
merge_all = U_p+C_p+L_p
if len(merge_all) > 1:
intersections[p] = []
for s in merge_all:
intersections[p].append(s)
merge_CL = C_p+L_p
merge_UC = U_p+C_p
for s in merge_CL:
# deletes at a point slightly above (to break ties) - where seg is located in tree
# above intersection point
t.delete(p, s)
# put segments into T based on where they are at y-val just below p[1]
for s in merge_UC:
n = getNextPoint(p, s, lower_check)
if n[0] > rightmost[0]:
rightmost = n
rightmost_seg = s
if n[0] < leftmost[0]:
leftmost = n
leftmost_seg = s
t.insert(p, s)
# means only L_p -> check newly-neighbored segments
if len(merge_UC) == 0:
neighbors = (t.get_left_neighbor(p), t.get_right_neighbor(p))
if neighbors[0] and neighbors[1]:
find_new_event(neighbors[0].value, neighbors[1].value, p, q)
# of newly inserted pts, find possible intersections to left and right
else:
left_neighbor = t.get_left_neighbor(p)
if left_neighbor:
find_new_event(left_neighbor.value, leftmost_seg, p, q)
right_neighbor = t.get_right_neighbor(p)
if right_neighbor:
find_new_event(right_neighbor.value, rightmost_seg, p, q)
def find_new_event(s1, s2, p, q):
i = intersect(s1, s2)
if i:
if compare_by_y(i, p) == 1:
if not q.find(i):
q.insert(i, [])
# segment is in ((x, y), (x, y)) form
# first pt in a segment should have higher y-val - this is handled in function
def intersection(S):
s0 = S[0]
if s0[1][1] > s0[0][1]:
s0 = (s0[1], s0[0])
q = Q(s0[0], [s0])
q.insert(s0[1], [])
intersections = {}
for s in S[1:]:
if s[1][1] > s[0][1]:
s = (s[1], s[0])
q.insert(s[0], [s])
q.insert(s[1], [])
t = T()
while q.key:
p, segs = q.get_and_del_min()
handle_event_point(p, segs, q, t, intersections)
return intersections# Test.py
# Test file for lsi.
# Author: Sam Lichtenberg
# Email: splichte@princeton.edu
# Date: 09/02/2013
from lsi import intersection
import random
import time, sys
from helper import *
ev = 0.00000001
def scale(i):
return float(i)
use_file = None
try:
use_file = sys.argv[2]
except:
pass
if not use_file:
S = []
for i in range(int(sys.argv[1])):
p1 = (scale(random.randint(0, 1000)), scale(random.randint(0, 1000)))
p2 = (scale(random.randint(0, 1000)), scale(random.randint(0, 1000)))
s = (p1, p2)
S.append(s)
f = open('input', 'w')
f.write(str(S))
f.close()
else:
f = open(sys.argv[2], 'r')
S = eval(f.read())
intersections = []
seen = []
vs = False
hs = False
es = False
now = time.time()
for seg1 in S:
if approx_equal(seg1[0][0], seg1[1][0], ev):
print 'VERTICAL SEG'
print ''
print ''
vs = True
if approx_equal(seg1[0][1], seg1[1][1], ev):
print 'HORIZONTAL SEG'
print ''
print ''
hs = True
for seg2 in S:
if seg1 is not seg2 and segs_equal(seg1, seg2):
print 'EQUAL SEGS'
print ''
print ''
es = True
if seg1 is not seg2 and (seg2, seg1) not in seen:
i = intersect(seg1, seg2)
if i:
intersections.append((i, [seg1, seg2]))
# xpts = [seg1[0][0], seg1[1][0], seg2[0][0], seg2[1][0]]
# xpts = sorted(xpts)
# if (i[0] <= xpts[2] and i[0] >= xpts[1]:
# intersections.append((i, [seg1, seg2]))
seen.append((seg1, seg2))
later = time.time()
n2time = later-now
print "Line sweep results:"
now = time.time()
lsinters = intersection(S)
inters = []
for k, v in lsinters.iteritems():
#print '{0}: {1}'.format(k, v)
inters.append(k)
# inters.append(v)
later = time.time()
print 'TIME ELAPSED: {0}'.format(later-now)
print "N^2 comparison results:"
pts_seen = []
highestseen = 0
for i in intersections:
seen_already = False
seen = 0
for p in pts_seen:
if approx_equal(i[0][0], p[0], ev) and approx_equal(i[0][1], p[1], ev):
seen += 1
seen_already = True
if seen > highestseen:
highestseen = seen
if not seen_already:
pts_seen.append(i[0])
in_k = False
for k in inters:
if approx_equal(k[0], i[0][0], ev) and approx_equal(k[1], i[0][1], ev):
in_k = True
if in_k == False:
print 'Not in K: {0}: {1}'.format(i[0], i[1])
# print i
print highestseen
print 'TIME ELAPSED: {0}'.format(n2time)
#print 'Missing from line sweep but in N^2:'
#for i in seen:
# matched = False
print len(lsinters)
print len(pts_seen)
if len(lsinters) != len(pts_seen):
print 'uh oh!'四、测试代码说明
for more information.
Usage:
from lsi import intersection
# S is a list of tuples of the form: ((x,y), (x,y))
i = intersection(S)
This function returns a dictionary of intersection points (keys) and a list of their associated segments (values).
Currently, this implementation does not handle horizontal/vertical line segments. This will be changed shortly!
A test file is available. It compares the running time of the algorithm to that of a brute-force O(N^2) comparison. It also generates a specified number of random input segments--you can set the precision and range by editing the file.
Email at: splichte@princeton.edu
五、关于使用python包
5.1 安装
python -m pip install --upgrade bentley_ottmann5.2 最新开发包安装
1、从 GitHub 存储库下载最新版本
git clone https://github.com/lycantropos/bentley_ottmann.git
cd bentley_ottmann2、安装依赖包
python -m pip install -r requirements.txt3、正式安装
python setup.py install5.3 测试代码
Usage
With segments
>>> from ground.base import get_context
>>> context = get_context()
>>> Point, Segment = context.point_cls, context.segment_cls
>>> unit_segments = [Segment(Point(0, 0), Point(1, 0)),
... Segment(Point(0, 0), Point(0, 1))]
we can check if they intersect
>>> from bentley_ottmann.planar import segments_intersect
>>> segments_intersect(unit_segments)
True
With contours
>>> Contour = context.contour_cls
>>> triangle = Contour([Point(0, 0), Point(1, 0), Point(0, 1)])
>>> degenerate_triangle = Contour([Point(0, 0), Point(2, 0), Point(1, 0)])
we can check if they are self-intersecting or not
>>> from bentley_ottmann.planar import contour_self_intersects
>>> contour_self_intersects(triangle)
False
>>> contour_self_intersects(degenerate_triangle)
True
1832
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
