【智能算法】花朵授粉算法（FPA）原理及实现

---

1.背景

2012年，Yang等人受到自然界花朵授粉过程启发，提出了鸭群算法（Flower Pollination Algorithm, FPA）。

2.算法原理

2.1算法思想

FPA基于自然界花朵授粉过程，主要分为两个阶段：全局授粉和局部授粉。

2.2算法过程

全局授粉

在全局授粉中，花粉由昆虫等传粉媒介携带。由于昆虫通常可以飞行和移动的范围更大，花粉可以传播很远的距离，这保证了最适者的授粉和繁殖：
$${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+L({\mathbf{x}}_i^t-{\mathbf{g}}_{\ast })\text{\hspace{1em}(1)}$$
其中，g*为最优授粉者。参数L是授粉的强度，本质上是一个步长。由于昆虫可能会以不同的距离步长进行长距离移动，这里采用莱维飞行模拟：
$$\begin{array}{r}L\sim \frac{\lambda \Gamma (\lambda )\sin (\pi \lambda /2)}{\pi }\frac{1}{s^{1+\lambda }},(s\gg s_0>0)\end{array}\text{\hspace{1em}(2)}$$

局部授粉

局部授粉可以表述为：
$${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+ϵ({\mathbf{x}}_j^t-{\mathbf{x}}_k^t)\text{\hspace{1em}(3)}$$
这里，xj,xk为xi领域中其他授粉者，参数为[0,1]随机数，实际进行局部随机游走。

伪代码

3.结果展示

使用测试框架，测试FPA性能 一键run.m

• 【智能算法】省时方便，智能算法统计指标——一键运行~

CEC2005-F9

箱型图

探索与开发

种群空间搜索图

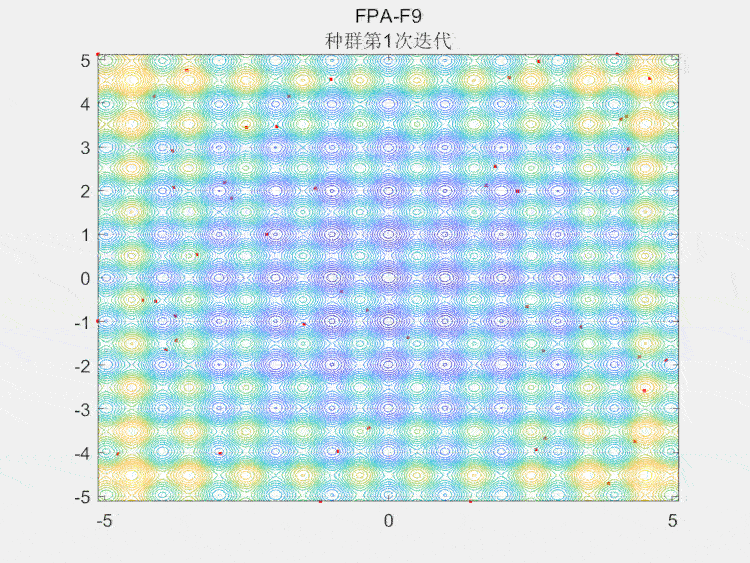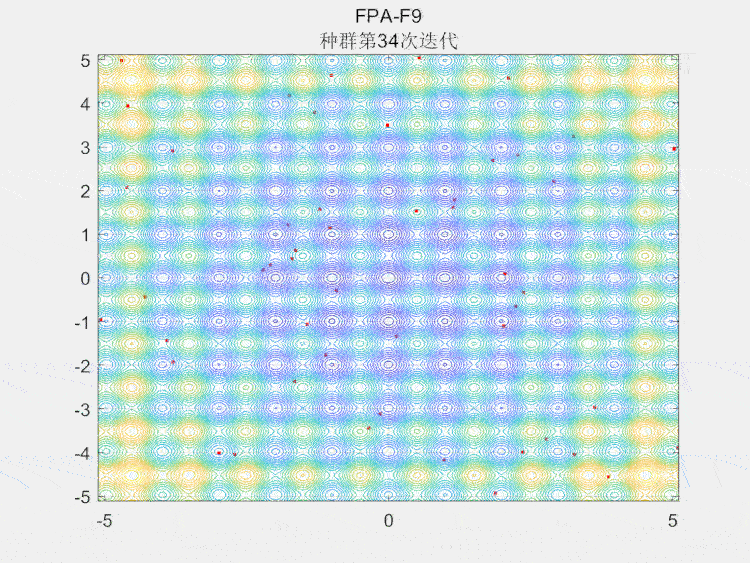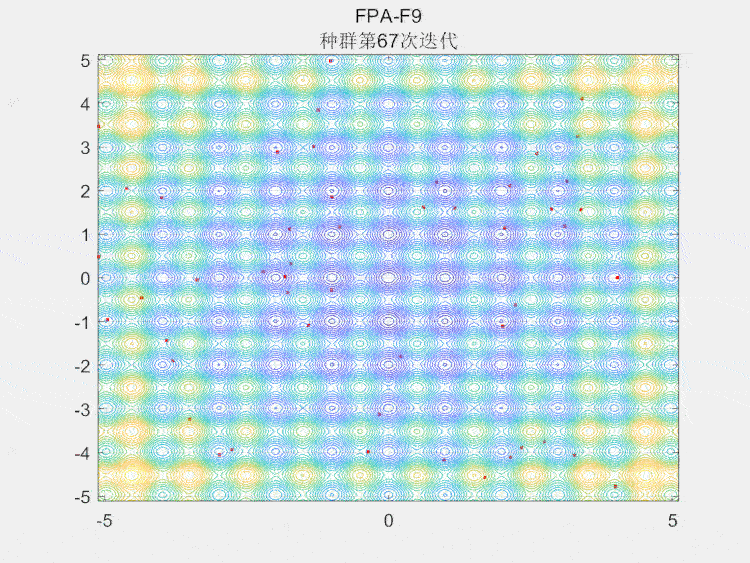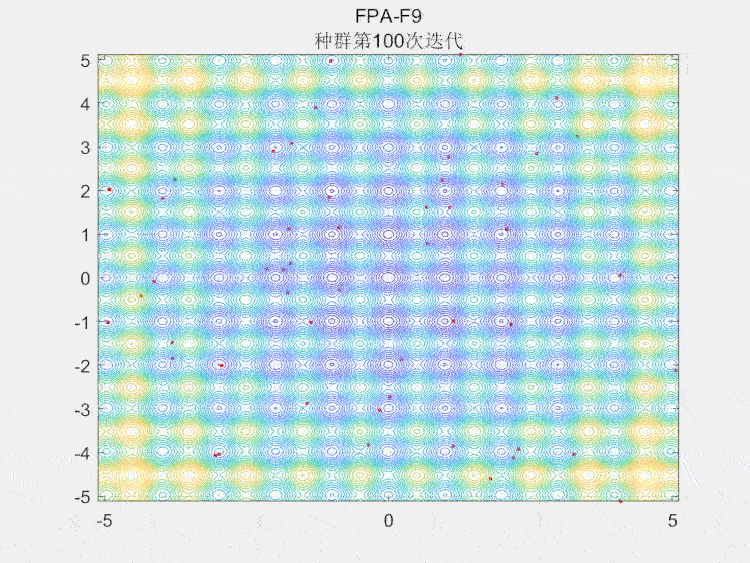
4.参考文献

[1] Yang X S. Flower pollination algorithm for global optimization[C]//International conference on unconventional computing and natural computation. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 240-249.