【智能算法】白鲸优化算法（BWO）原理及实现

小O的算法实验室

已于 2024-08-30 23:08:20 修改

阅读量3.2k

点赞数 21

分类专栏：智能算法文章标签：算法智能算法

于 2024-05-20 23:46:39 首次发布

本文链接：https://blog.csdn.net/Logic_9527/article/details/139074721

版权

智能算法专栏收录该内容

490 篇文章

订阅专栏

1.背景

2022年，C Zhong受到自然界白鲸行为启发，提出了白鲸优化算法（Beluga Whale Optimization, BWO）。

在这里插入图片描述

2.算法原理

2.1算法思想

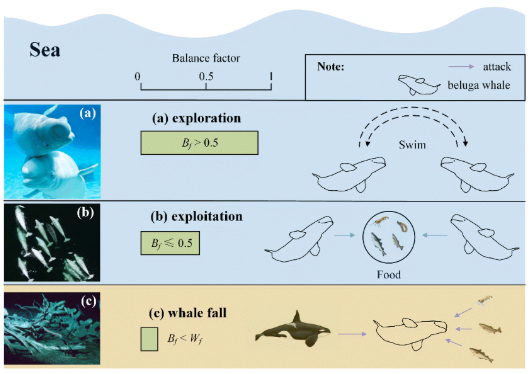
BWO算法模拟了白鲸的行为，如游泳、捕食和鲸鱼坠落。BWO包含探索阶段和开发阶段。探索阶段通过随机选择白鲸来保证设计空间的全局搜索能力，开发阶段控制设计空间的局部搜索能力。

在这里插入图片描述

2.2算法过程

BWO算法可以根据平衡因子Bf从探索过渡到开发:
$B_f=B_0(1-T/2T_{max})\tag{1}$

探索阶段

BWO的探索阶段是通过考虑白鲸的游泳行为来建立:
$\begin{cases}X_{i,j}^{T+1}=X_{i,p_{j}}^{T}+\left(X_{r,p_{1}}^{T}-X_{i,p_{j}}^{T}\right)(1+r_{1})\sin\left(2\pi r_{2}\right),&j=even\\X_{i,j}^{T+1}=X_{i,p_{j}}^{T}+\left(X_{r,p_{1}}^{T}-X_{i,p_{j}}^{T}\right)(1+r_{1})\cos\left(2\pi r_{2}\right),&j=odd\end{cases}\tag{2}$
其中，sin(2πr2)和cos(2πr2)表示镜像白鲸的鳍朝向水面，根据奇数和偶数选择的维度，更新后的位置反映了白鲸在游泳或潜水时的同步或镜像行为。

开发阶段

BWO的开发阶段灵感来自于白鲸的捕食行为，白鲸可以根据附近白鲸的位置合作觅食和移动:
$X_{i}^{T+1}=r_{3}X_{best}^{T}-r_{4}X_{i}^{T}+C_{1}\cdot L_{F}\cdot\left(X_{r}^{T}-X_{i}^{T}\right)\tag{3}$
其中，LF是莱维飞行步长。

鲸落行为

少数白鲸坠落深海，滋养生物，形成“鲸鱼坠落”现象。鲨鱼和无脊椎动物聚集食用尸体，吸引毛甲壳类动物。骨骼最终被细菌和珊瑚分解。模拟鲸鱼掉落行为，选择掉落概率模拟微小变化。确保种群数量不变，通过白鲸位置和鲸落步长更新位置:
$X_i^{T+1}=r_5X_i^T-r_6X_r^T+r_7X_{step}\tag{4}$
其中r5, r6, r7为(0,1)之间的随机数，Xstep为鲸鱼下降的步长:
$X_{step}=(u_b-l_b)\exp{(-C_2T/T_{\max})}\tag{5}$
其中，C2为与鲸鱼下降概率和种群规模相关的阶跃因子(C2 = 2Wf×n)，鲸鱼坠落的概率(Wf)计算为线性函数:
$W_f=0.1-0.05T/T_{\max}\tag{6}$