【智能算法】三角拓扑聚合优化算法（TTAO）原理及实现

---

1.背景

2024年，S Zhao受到数学相似三角形拓扑结构启发，提出了三角拓扑聚合优化算法（Triangulation Topology Aggregation Optimizer, TTAO）。

2.算法原理

2.1算法思想

TTAO算法包含两种策略：泛化聚合和局部聚合，迭代构建多个相似的三角形拓扑单元，以平衡探索和开发。前者通过不同三角拓扑单元之间的正信息交换产生新的顶点，后者根据每个单元的局部最优顶点在有希望的位置构造新的单元。

2.2算法过程

三角拓扑单元形成

在球坐标系中以第一个顶点为起始顶点，利用三角函数将其转换为普通坐标系，得到一个长度为l*f的新方向向量。生成的长度为 l *f 的方向向量逆时针旋转π/3，然后通过坐标系变换得到第三个顶点:
$$\begin{array}{rl}\overrightarrow{X_{i,2}}& =\overrightarrow{X_{i,1}}+l\ast \overrightarrow{f(\theta )}\\ \overrightarrow{X_{i,3}}& =\overrightarrow{X_{i,1}}+l\ast \overrightarrow{f\left(\overrightarrow{\theta +\frac{\pi }{3}}\right)}\end{array}\text{\hspace{1em}(1)}$$
其中l表示三角形拓扑单元的大小:
$$l=9\ast e^{-\frac{t}{T}}\text{\hspace{1em}(2)}$$
在早期阶段，l可以产生更大的搜索范围，以专注于全局探索。然后在后期聚集后，向有希望的方向深入发展。为了保证在以后的迭代中仍能产生三角拓扑单元，l不会减小到0:
$$\begin{gathered} \overrightarrow{f\left(\overrightarrow{\theta }\right)}=[\cos {\theta }_1,\cos {\theta }_2,...,\cos {\theta }_{D-1},\cos {\theta }_D] \\ \overrightarrow{f\left(\overrightarrow{\theta +\frac{\pi }{3}}\right)}=\left[\cos \left({\theta }_1+\frac{\pi }{3}\right),\dots ,\cos \left({\theta }_{D-1}+\frac{\pi }{3}\right),\cos \left({\theta }_D+\frac{\pi }{3}\right)\right]\text{\hspace{1em}(2)} \end{gathered}$$
每组三角拓扑单元在内部聚合为第四个顶点:
$$\overrightarrow{X_{i,4}}=r_1\ast \overrightarrow{X_{i,1}}+r_2\ast \overrightarrow{X_{i,2}}+r_3\ast \overrightarrow{X_{i,3}}\text{\hspace{1em}(3)}$$
其中r1, r2, r3为[0,1]之间的随机数，r1+r2+r3 = 1。因此，第四个搜索代理位于每个三角形拓扑单元内。在每次迭代开始时，从一个相同长度的顶点和两条相同长度的边得到新的相似三角形拓扑单元。

泛化聚合

泛化聚合强调探索阶段，其收集不同三角单元中优秀个体的信息，并创造出新的可行解。信息交互发生在每个三角拓扑单元中最优个体与任意选定单元集中最优个体之间。受到遗传算法中基因交叉的启发，新个体在较好的两顶点连接中产生:
$$\overrightarrow{X_{i,new1}^{t+1}}=r_4\ast \overrightarrow{X_{i,best}^t}+(1-r_4)\ast \overrightarrow{X_{rand,best}^t}\text{\hspace{1em}(4)}$$

其中，Xi,best，Xrand,best分别代表单元i最佳个体和第t次迭代最优个体。
$$\{\begin{array}{ll}\overrightarrow{X_{i,best}^{t+1}}=\overrightarrow{X_{i,new1}^{t+1}}& f_{\overrightarrow{X_{i,new1}^{t+1}}}<f_{\overrightarrow{X_{i,best}^t}}\\ \overrightarrow{X_{i,sbes{t}^{t+1}}}=\overrightarrow{X_{i,new1}^{t+1}}& f_{\overrightarrow{X_{i,new1}^{t+1}}}<f_{\overrightarrow{X_{i,sbes{t}^t}}}\end{array}\text{\hspace{1em}(5)}$$

局部聚合

局部聚合主要强调开发阶段，三角形拓扑单元在内部聚集。在前一阶段之后，更新后的最优或次优个体与适应度值较好的群体中的两个顶点之间临时形成三角形拓扑:
$$\overrightarrow{X_{i,new2}^{t+1}}=\overrightarrow{X_{i,best}^{t+1}}+\alpha \ast \left(\overrightarrow{X_{i,best}^{t+1}}-\overrightarrow{X_{i,sbest}^{t+1}}\right)\text{\hspace{1em}(6)}$$
其中α递减，调整聚合范围大小：
$$\alpha =\ln \left(\frac{e-e^3}{T-1}t+e^3-\frac{e-e^3}{T-1}\right)\text{\hspace{1em}(7)}$$
使用次优个体信息的目的是防止最优个体陷入局部极值，应保证临时三角单元的导点在单元内最优：
$$\overrightarrow{X_{i,best}^{t+1}}=\{\begin{array}{ll}\overrightarrow{X_{i,new2}^{t+1}}& f_{\overrightarrow{X_{i,new2}^{t+1}}}<f_{\overrightarrow{X_{i,best}^{t+1}}}\\ \overrightarrow{X_{i,best}^{t+1}}& otherwise\end{array}\text{\hspace{1em}(8)}$$

伪代码

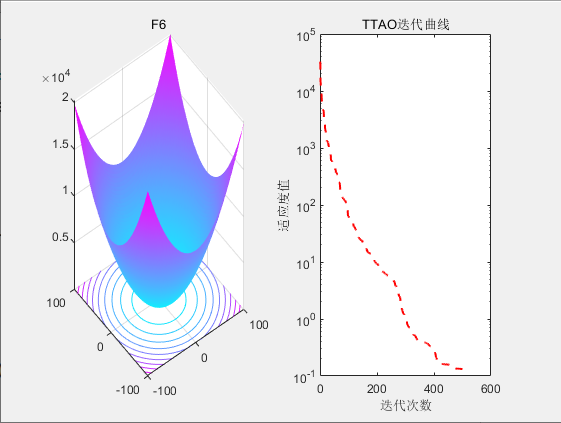
3.结果展示

4.参考文献

[1] Zhao S, Zhang T, Cai L, et al. Triangulation topology aggregation optimizer: A novel mathematics-based meta-heuristic algorithm for continuous optimization and engineering applications[J]. Expert Systems with Applications, 2024, 238: 121744.

5.代码获取